1과목: 과목 구분 없음
1. 반지름이 R[m]인 드럼이 N[rpm]으로 회전하면서 무게 FW[N]인 추를 H[m] 들어 올리고자 할 때, 필요한 동력[W]은?
2. 플라이휠(flywheel)에 대한 설명으로 옳지 않은 것은?
- 내연기관, 왕복펌프, 공기압축기 등에서 흔히 사용된다.
- 구동토크가 많이 발생하면 운동에너지를 흡수하여 각속도 증가량이 둔화된다.
- 동일 4행정기관에서는 직렬 기통 수가 많아질수록 에너지 변동계수도 커지므로 이를 고려하여 설계하여야 한다.
- 축적된 운동에너지를 전단기 및 프레스 등의 작업에너지로 사용할 수 있으며, 그 출력은 극관성모멘트의 크기에 따라 결정된다.
3. 그림과 같은 리벳이음에서 6000 [N]의 하중(F)이 작용할 때, 가장 왼쪽의 리벳에 작용하는 전단력의 크기[N]와 방향은?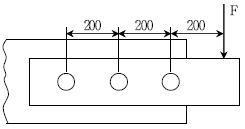
- 8000, ↑
- 8000, ↓
- 4000, ↑
- 4000, ↓
4. 인장항복응력이 400 [MPa]인 재료가 σx=120 [MPa], σy=-80 [MPa]인 평면응력상태에 있을 때, 최대 전단응력설에 따른 안전계수는?
- 6
- 4
- 3
- 2
5. 비틀림 모멘트 T가 작용하면 비틀림각이 4 ° 발생하는 지름 d인 축에서 축지름만 변경하여 비틀림각을 1 °로 줄이고자 할 때, 축지름[mm]은? (단, 축은 실축이고, 탄성 거동한다고 가정한다)
6. 그림과 같이 필렛 용접된 두 금속판의 좌우로 10 [kN]의 하중이 가해질 때, 필요한 용접부 최소 길이 m, n에 가장 근사한 치수[mm]는? (단, 용접부의 허용전단응력은 10 [N/mm2]이다) (순서대로 m, n)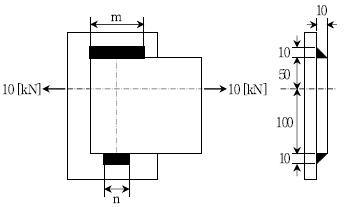
- 188, 94
- 137, 69
- 110, 55
- 95, 48
7. 아이볼트에 축방향으로 3 [kN]의 인장하중이 작용할 때, 사용 가능한 볼트의 최소 바깥지름[mm]은? (단, 허용인장응력은 40 [N/mm2], 골지름(d1)과 바깥지름(d)의 비율 d1/d=0.5, π=3으로 한다)
- 10
- 12
- 16
- 20
8. 사각나사의 안지름이 8 [mm], 바깥지름이 12 [mm], 피치는 π[mm]일 때, 1000 [N]의 축방향 하중을 견딜 수 있는 너트의 최소 높이[mm]는? (단, 재료의 허용접촉면압력은 10 [N/mm2]이다)
- 1
- 5
- 10
- 12
9. 스프링지수가 10이고 소선의 지름이 2 [mm]인 압축 코일스프링에서 하중이 70 [kgf]에서 50 [kgf]로 감소할 때 처짐의 변화가 50 [mm]가 되는 스프링의 유효감김수는? (단, 전단탄성계수는 8 × 103 [kgf/mm2]이다)
- 5
- 6
- 7
- 8
10. 벨트 전동에서 벨트의 장력으로 인해 베어링에 전달되는 하중(Fd)과 이완측 장력(Ts) 사이의 관계(Fd/Ts)로 옳은 것은? (단, 마찰계수는 μ이고, 벨트의 접촉각은θ 이며, 원심력의 영향은 무시한다)
11. 그림과 같이 지름이 d인 축에 평행키가 있을 때, 중심으로부터 L만큼 떨어져 있는 레버에 작용할 수 있는 최대 힘 F는? (단, 키의 너비, 깊이, 길이는 각각 b, h, l 이고 단면에 작용하는 허용전단응력은 T0 이다)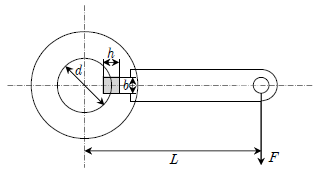
12. 헬리컬 기어(helical gear)의 특징으로 옳지 않은 것은?
- 이가 잇면을 따라 연속적으로 접촉하므로 이의 물림길이가 길다.
- 두 기어의 비틀림각의 방향이 반대이고 각의 크기가 서로 다를 경우, 축은 평행하지 않고 교차한다.
- 최소 잇수가 평기어보다 적기 때문에 잇수가 적은 기어에서 사용된다.
- 임의로 비틀림각을 선정할 수 있으나 두 기어의 중심거리를 조정할 수 없다.
13. 구멍의 공차역은 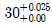 축의 공차역은
축의 공차역은 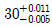 때, 이 축과 구멍의 결합에 대한 설명으로 옳은 것은?
때, 이 축과 구멍의 결합에 대한 설명으로 옳은 것은?
- 최대죔새는 0.011이다.
- 최대틈새는 0.014이다.
- 최소틈새는 0.014이다.
- 억지 끼워맞춤이다.
14. 지름이 D[mm], 허용선접촉압력이 p0[kgf/mm], 마찰계수가 μ인 마찰차를 사용하여 N[rpm]의 회전속도로 동력 H[PS]를 전달하기 위해 필요한 마찰차의 최소 너비 b[mm]는? (단, 맞물린 두 마찰차 사이에 상대운동은 없다)
15. 태양기어 1개, 유성기어 3개인 유성기어장치에서 내접기어를 고정할 때, 태양기어에 대한 캐리어의 각속도비는? (단, 기어는 표준기어를 사용하고, 태양기어 잇수는 20개, 유성기어의 잇수는 40개이다)
- 1/4
- 1/5
- 1/6
- 1/8
16. 그림과 같이 차동피니언 잇수 24개, 측면기어 잇수 36개인 차동기어 장치에서 왼쪽 측면기어의 회전속도가 40 [rpm]이고, 오른쪽 측면 기어의 회전속도가 50 [rpm]일 때, 차동피니언의 회전속도[rpm]는?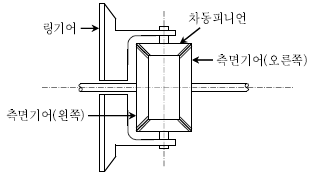
- 7.5
- 10
- 15
- 20
17. 공작물의 표면거칠기가 다음과 같은 삼각파형으로 측정되었을 때, 해당 공작물의 중심선 평균거칠기(Ra)[μm]는? (단, d=8 [μm]이며 l=80 [μm]이다)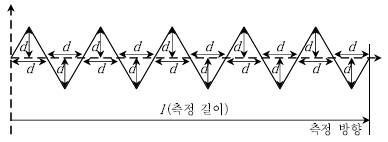
- 2
- 4
- 6
- 8
18. 내식성, 내압성, 경제성이 우수하여 가스압송관, 광산용 양수관 등에 가장 많이 사용하는 관은?
- 강관
- 주철관
- 비철금속관
- 비금속관
19. 바깥지름이 D, 두께가 t이며 양단이 고정되어 있는 강관이 초기온도 T0에서 T로 가열되었을 때, 강관에 발생하는 축방향 압축력은? (단, 선열팽창계수는 α, 탄성계수는 E이다)
- απE(T-T0)(Dt-2t2)/2
- απE(T-T0)tD2/4
- απE(T-T0)tD
- απE(T-T0)(tD-t2)
20. 나선면의 마찰각이 7 °, 리드각이 3 °인 사각나사를 조일 때의 효율은? (단, 사각나사의 자리면 마찰을 무시하고, tan(3 °)≒0.05, tan(4 °)≒0.07, tan(7 °)≒0.12, tan(10 °)≒0.18로 근사하여 계산한다)
- 2/8
- 7/12
- 7/18
- 5/18





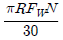
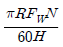
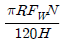
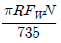

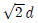
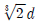
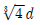
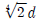
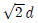 "이다.
"이다.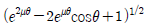
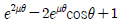
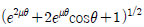
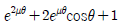
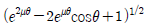 "이 정답이다.
"이 정답이다.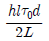
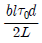
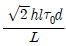

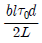 "이다.
"이다.
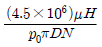
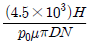
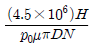
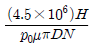 "이다.
"이다.
필요한 동력 = FW × H × 2π × N / 60
여기서 2π × N / 60은 회전하는 드럼의 속도를 라디안/초 단위로 나타낸 것입니다. 따라서 정답은 "