1과목: 과목 구분 없음
1. 다음 중 뉴턴의 운동법칙에 해당하지 않는 것은?
- 물체에 작용하는 힘이 평형을 이룬다면 정지해 있는 물체는 계속 정지해 있고 움직이던 물체는 등속도 직선 운동을 한다.
- 마찰력은 두 물체의 접촉면에서 발생하며 그 힘의 방향은 물체의 운동방향과 반대이다.
- 움직이는 물체의 가속도 크기는 작용하는 힘에 비례하고 물체의 질량에 반비례하며 방향은 힘의 방향과 같다.
- 임의의 물체에 작용하는 작용힘과 반작용힘은 그 크기가 같고 방향이 서로 반대이며 동일선상에 있다.
2. 다음 설명 중에서 옳지 않은 것은?
- 힘을 표시하는 3요소는 힘의 크기, 방향, 작용점이다.
- 선형 탄성영역에서는 응력과 변형률이 비례한다.
- 동마찰계수는 정마찰계수보다 작다.
- 힘, 변위, 속력, 가속도는 모두 벡터(vector)양이다.
3. 단면의 성질에 관한 설명으로 옳지 않은 것은?
- 단면 2차 모멘트는 항상 양(+)의 값이다.
- 동일 단면적의 도심축에 대한 단면 2차 모멘트는 정삼각형이 정사각형보다 크다.
- 대칭축은 항상 주축이다. 그러나 주축이 항상 대칭축인 것은 아니다.
- 단면 1차 모멘트는 그 단면의 도심축에 대한 값이 최대이다.
4. 길이 150mm, 지름 15mm의 강봉에 인장력을 가했더니 길이 방향으로 1.0mm가 늘어났다면 지름의 변화량[mm]은? (단, 이 강봉의 포아송수는 4이다)
- 0.025 (감소)
- 0.025 (증가)
- 0.050 (감소)
- 0.050 (증가)
5. 다음의 보가 정정 구조물이 되기 위해 필요한 내부힌지의 개수는?
- 필요 없다
- 1개
- 2개
- 3개
6. 그림과 같은 구조물에서 BC부재가 100 kN의 인장력을 받을 때 하중 P의 값[kN]은?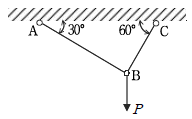
- 100.0
- 115.5
- 141.4
- 173.2
7. 다음과 같은 응력-변형률 곡선에 관한 설명으로 옳지 않은 것은?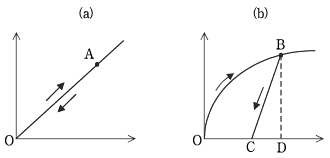
- 그림 (a)에서 하중을 받아 A점에 도달한 후 하중을 제거했을 때 OA곡선을 따라 O점으로 되돌아가는 재료의 성질을 선형 탄성(linear elasticity)이라 한다.
- 그림 (b)에서 하중을 받아 B점에 도달한 후 하중을 제거했을 때 OB곡선을 따라 되돌아가지 않고 BC를 따라 C점으로 돌아가는 재료의 성질을 비선형 탄성(nonlinear elasticity)이라 한다.
- 그림 (b)에서 B점에 도달한 후 하중을 제거했을 때 발생한 변형률 OC를 잔류변형률(residual strain)이라 하고 변형률 CD를 탄성적으로 회복된 변형률이라 한다.
- 그림 (b)에서 B점에서 하중을 완전히 제거한 후 다시 하중을가하면 CB곡선을 따라 응력과 변형률이 발생된다.
8. A단이 고정 지지된 원형봉에 인장력 30kN이 작용하여 그림과 같은 신장량 △가 발생하였다면 이 재료의 탄성계수[GPa]는? (단, 계산의 편의상 원주율 π=3으로 한다)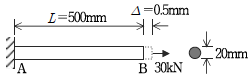
- 50
- 100
- 150
- 200
9. 다음 설명 중에서 옳지 않은 것은?
- 평형방정식의 수보다 많은 미지의 힘을 갖는 구조물을 부정정 구조물이라 부른다.
- 기하학적 불안정은 구조물의 반력 성분이 외적 안정을 확보할 수 있도록 적절하게 배열되어 있지 않거나 구속되지 않는 경우를 말한다.
- 트러스 구조물에서 부재의 수와 반력의 수의 합이 절점 수의 2배보다 작으면 부정정 트러스 구조물이다.
- 구조물을 적절하게 구속하기 위해서는 반력의 작용선들이 동일한 점에서 교차되지 않도록 해야 한다.
10. 다음 부정정보의 B단에 모멘트를 작용시킬 때, A단에 전달되는 모멘트(MA)는 B단의 작용 모멘트(MB)의 몇 배가 되는가? 단, E: 탄성계수, I: 단면 2차 모멘트)
- 0.5배
- 1.0배
- 1.5배
- 2.0배
11. 다음의 구조형식 중 구조 계산 시 부재들이 축방향력만을 받는 것으로 가정되는 구조형식은?
- 보
- 트러스
- 라멘
- 아치
12. 다음 그림은 임의의 하중이 가해지고 있는 단순보의 전단력선도이다. 최대 휨모멘트[kNㆍm]는?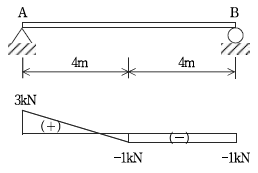
- 3.0
- 3.5
- 4.0
- 4.5
13. 단순보 CD에 발생하는 최대 휨모멘트[kNㆍm]는?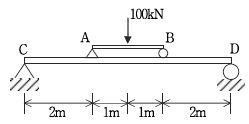
- 50
- 75
- 100
- 150
14. 단순 지지된 트러스에서 부재 A, B의 부재력[kN]은? (순서대로 A, B)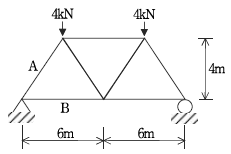
- 5(압축), 3(인장)
- 5(인장), 3(압축)
- 3(압축), 5(인장)
- 3(인장), 5(압축)
15. 단면이 폭 300mm, 높이 500mm인 단순보의 중앙 지간에 집중 하중 10 kN이 작용하고 있다. 이 구조물에서 생기는 최대 휨응력(σmax[MPa])은?
- σmax=1
- σmax=2
- σmax=100
- σmax=200
16. 다음 그림은 임의의 하중을 받는 단순보의 전단력선도이다. 옳지 않은 것은? (단, 보의 자중은 고려하지 않는다)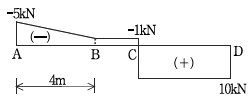
- AB 구간에는 1 kN/m의 등분포하중이 작용한다.
- CD 구간에는 하중이 작용하지 않는다.
- 전단력선도에서 (+)부 면적과 (-)부 면적은 같다.
- B점에 집중하중이 작용한다.
17. 아래 그림과 같이 스프링 상수가 각각 k1, k2인 부재 AD와 BF가 길이 L인 단순보 AB를 지지하는 구조물에서 A점으로부터 L/2만큼 떨어진 C점에 수직 하중 P가 작용하고 있다. 하중 재하점의 수직처짐 δ는? (단, 보 AB의 휨강성은 EI이며 보의 축변형 및 전단변형은 무시한다)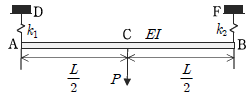
18. 오일러-베르누이 가정이 적용되는 균일단면 보의 응력에 관한 설명으로 옳은 것은?
- 휨을 받는 단면에 발생하는 법선(단면에 수직) 응력은 단면 계수에 비례한다.
- 직사각형 단면 내 전단응력은 단면의 상ㆍ하 끝단에서 최대 이다.
- 휨을 받는 단면에 발생하는 법선(단면에 수직) 변형률은 중립축으로부터의 거리에 비례한다.
- 단면이 I형인 경우 복부판(web)과 평행한 수직방향 하중이 작용할 때 단면에 작용하는 전단응력의 방향은 모두 수직방향 (수직전단응력)이다.
19. 그림과 같이 휨강성 EI가 일정한 단순보에 등분포 하중 ω가 작용할 때 최대처짐각 θ와 최대처짐량 δ는? (순서대로 θ, δ)
20. 기둥에 관한 설명으로 옳지 않은 것은?
- 기둥은 세장비에 따라 단주, 중간주, 장주로 구분할 수 있다.
- 단주에 편심 압축하중이 단면의 핵(core) 안에 작용하면 단면 내 어느 점에서도 인장응력이 발생하지 않는다.
- 기둥의 세장비는 기둥단면의 단면적, 단면 2차 모멘트, 그리고 기둥의 길이로 계산된다.
- 장주의 양단이 핀 지지되지 않은 경우의 탄성 좌굴 하중은 양단이 핀 지지된 장주의 오일러 공식에 유효길이(effective length)를 사용하여 구할 수 있으며 양단이 고정된 장주의 유효길이 계수(effective length factor)는 0.7이다.






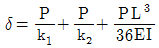
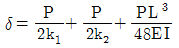
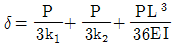

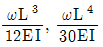
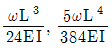
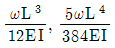

마찰력은 두 물체의 접촉면에서 발생하며 그 힘의 방향은 물체의 운동방향과 반대이다. 이유는 마찰력은 물체가 움직이는 방향과 반대 방향으로 작용하여 물체의 운동을 저해하기 때문이다. 예를 들어, 자동차가 길을 달리면 바퀴와 도로 사이에 마찰력이 발생하여 자동차의 속도를 감소시키는 역할을 한다.