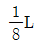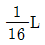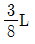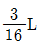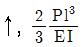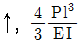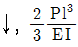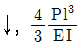1과목: 과목 구분 없음
1. 다음 그림과 같은 내민보에서 C점에 대한 전단력의 영향선에서 D점에 대한 종거는?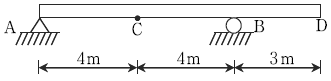
- -0.156
- -0.264
- -0.375
- -0.557
2. A점이 회전(hinge), B점이 이동(roller) 지지이고 부재의 길이가 L인 단순보에서, A지지점에서 중앙 C점(L/2)까지 작용하는 하중이 등분포하중일 때, 부재길이 L내에서 전단력이 제로(0)인 점은 A지지점에서 중앙쪽으로 얼마만큼 떨어진 곳에 위치하고 있는가?
3. 다음 그림과 같은 보에서 지점 B의 반력이 4P일 때 하중 3P의 재하위치 x는?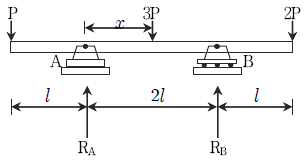
- x=l
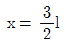
- x=2l
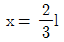
4. 다음 그림과 같은 켄틸레버보에서 Mo=2Pl인 경우 B점의 처짐방향과 처짐량 δ는? (단, 휨강성 EI는 일정하다)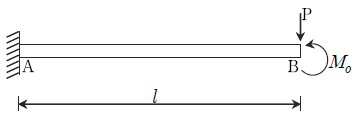
5. 다음 그림과 같은 탄소성 재료로 된 직사각형 단면보의 거동에 관한 설명 중 옳지 않은 것은?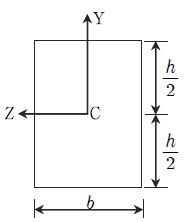
- 소성계수
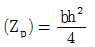 이다.
이다. - 소성모멘트
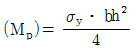 이다.
이다. - 항복모멘트
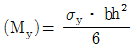 이다.
이다. - 형상계수
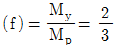 이다.
이다.
6. 길이가 4.0 m이고 직사각형 단면을 가진 기둥이 있다. 세장비 λ는? (단, 기둥의 단면성질에서 I max=2,500 cm4, Imin=1,600 cm4, A =100cm2이다)
- 50
- 80
- 100
- 160
7. 다음 그림과 같은 트러스에서 CF에 발생하는 부재력[kN]은?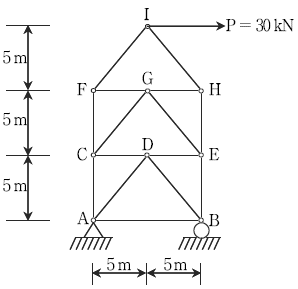
- 30 (압축)
- 30 (인장)
- 15 (압축)
- 15 (인장)
8. 다음 그림과 같은 게르버보(Gerber beam)에서 A점의 휨모멘트 값[tfㆍm]은?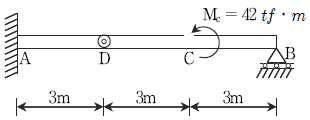
- -21
- 21
- -9
- 9
9. 다음 그림과 같이 철근 콘크리트로 만든 사각형 기둥의 단면 중심축에 의 압축 하중이 작용하고 있다. 콘크리트와 철근의 단면적이 각각 900cm2와 27cm2일 때, 콘크리트의 응력(σc)과 철근의 응력(σs)은?(단, 철근과 콘크리트의 탄성계수비(Es/Ec)는 9이고, 소수점이하는 반올림한다) (순서대로 σc[kgf/cm2], σs[kgf/cm2])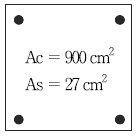
- 105, 925
- 105, 945
- 125, 925
- 125, 945
10. 변위일치의 방법을 이용하여 양단고정보를 해석하고자 할 때, 잉여미지반력의 개수는? (단, 보의 수평반력은 없다고 가정한다)
- 1개
- 2개
- 3개
- 4개
11. 다음 그림과 같이 방향이 반대인 힘 P와 3P가 L간격으로 평행하게 작용하고 있다. 두 힘의 합력의 작용위치 X는?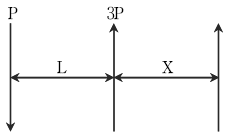
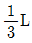
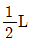
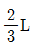
- L
12. 다음은 ‘우력’에 대한 약술이다. ( )에 들어갈 단어를 바르게 연결한 것은? (순서대로 ㉠, ㉡, ㉢)
- 같고, 반대방향, 회전운동
- 다르고, 반대방향, 회전운동
- 다르고, 같은방향, 평행운동
- 같고, 같은방향, 평행운동
13. 다음 그림과 같이 단면적이 200cm2인 임의의 도형이 있다. 도형의 도심에서 10 cm만큼 떨어진 X1축에서의 단면2차모멘트가 Ix1= 25,000 cm4일 때, 20 cm만큼 떨어진 X2축에서의 단면2차모멘트는?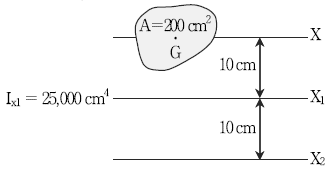
- 45,000 cm4
- 65,000 cm4
- 85,000 cm4
- 105,000 cm4
14. 축강성이 EA인 다음 강철봉의 C점에서의 수평변위는? (단, EA는 일정하다)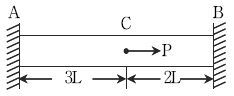
- 4PL/5EA
- PL/EA
- 6PL/5EA
- 7PL/5EA
15. 다음 그림과 같은 부재와 강체 벽체와의 간격이 0.1 mm이고, 단면적이 50 cm2, 길이가 1.0 m인 부재가 있다. 온도가 40 °C 상승할 때 이 부재에 발생하는 응력[GPa]은? (단, 부재의 열팽창계수(α)는 15 × 10-6 / °C, 탄성계수(E)는 200GPa 이다)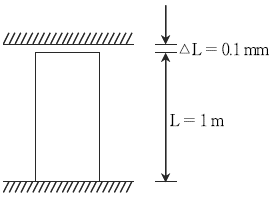
- 0.1
- 0.2
- 0.4
- 0.8
16. 다음 그림과 같은 단면적 1 cm2, 길이 1 m인 철근 AB부재가 있다. 이 철근이 최대 δ=1.0 cm 늘어날 때 이 철근의 허용하중 P[kN]는? (단, 철근의 탄성계수(E)는 2.1 × 104 kN/cm2로 한다)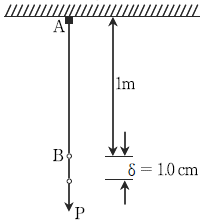
- 160
- 180
- 210
- 240
17. 길이가 10 m이고 지름이 50 cm인 강봉이 길이방향으로 작용하는 인장력에 의하여 길이방향으로 변형이 10 cm 발생하였다. 이때 강봉의 포와송비(Poisson's ratio)가 0.2인 경우, 강봉의 반지름[cm] 변화로 옳은 것은?
- 0.1 증가
- 0.1 감소
- 0.05 증가
- 0.05 감소
18. 다음 그림과 같은 부정정보에서 지점 A의 처짐각(θA) 및 수직 반력(RA)은? (단, 휨강성 EI는 일정하다)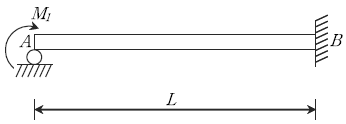
19. 다음 그림과 같은 결합도르래를 이용하여 500 kN의 물체를 들어 올릴 때 필요한 힘 T[kN]는? (단, 도르래의 무게는 무시한다)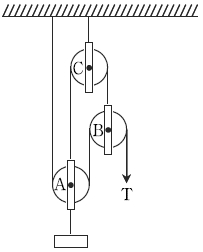
- 25
- 125
- 250
- 500
20. 다음 그림과 같은 구조물의 중앙 C점에서 휨모멘트가 0이 되기 위한 a/ℓ의 비는? (단, P=2wℓ이다)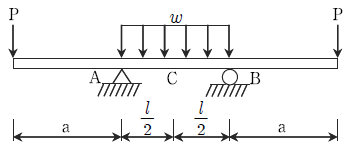
- 1/4
- 1/6
- 1/8
- 1/16