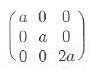1과목: 기하광학 및 광학기기
1. 다음 수차 중 bending에 의한 수차교정이 가능한 것들로만 짝지어진 것은?
- Spherical aberration, Coma
- Oblique astigmatism, Distortion
- Curvature of field, Distortion
- Spherical aberration, Chromatic aberration
2. 다음 그림은 어떤 수차를 설명하기 위한 것인가?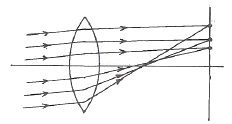
- Coma
- Distortion
- Spherical aberration
- Oblique astigmatism
3. 곡률반경이 큰 볼록 구면경의 곡률반경 r을 그림과 같은 장치로 측정할 때 볼록거울의 정점으로부터 물체슬릿까지의 거리가 D, 슬릿으로부터 나온 광속의 볼록거울 접촉면에서의 폭을 ℓ, 슬릿이 놓여 있는 평면상에서의 광속의 폭이 L일 때 곡률반경 r은?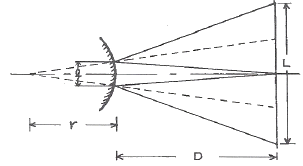
- 2Dℓ/(L-2ℓ)
- 2Dℓ/(L+2ℓ)
- Dℓ/(L-2ℓ)
- Dℓ/(L+2ℓ)
4. 공기중에서 파장이 600nm인 빛이 굴절률 1.5인 매질 내로 입사하였을 때 매질 내에서의 파장(λ)과 진동수(f)의 값은?
- λ=400nm, f=5×1014Hz
- λ=400nm, f=7.5×1014Hz
- λ=90nm, f=5×14Hz
- λ=900nm, f=7.5×14Hz
5. 반사경을 이용한 광학계의 장점에 관한 내용으로 틀린 것은?
- 가공성이 좋다.
- 무게를 줄일 수 있다.
- f-수를 크게 할 수 있다.
- 색수차를 제거할 수 있다.
6. 밝기 9의 밝은 선과 밝기 1의 어두운 선이 주기적으로 반복되는 sinusoidal pattern이 있다. 이 pattern을 광학계로 1/2로 축소하여 결상하였을 때, 가장 밝은 부분의 밝기는 12, 가장 어두운 부분의 밝기는 8이 되었다. 이 광학계의 MTF는 얼마인가?
- 0.25
- 0.5
- 0.75
- 2
7. 얇은 렌즈에 대한 초점거리 공식을 사용한 굴절률이 1.52, 곡률반경이 25mm인 평볼록렌즈의 초점길이는 약 몇 cm 인가?
- 4.8
- 9.6
- 14.4
- 19.2
8. 유효초점거리 100mm, 입사동의 직경이 20mm인 무수차 원형개구 광학계로 무한대에 있는 물체를 결상하였다. 빛의 파장이 0.5㎛일 때, 이 광학계가 분해할 수 있는 최대 공간주파수(cutoff frequency)는 몇 cycles/mm인가?
- 200
- 400
- 500
- 1000
9. 1mm당 10개의 줄무늬가 있는 물체에 대한 두 광학계의 MTF 값이 각각 0.7과 0.8이다. 두 광학계를 동시에 사용할 때, 전체 MTF값은?(오류 신고가 접수된 문제입니다. 반드시 정답과 해설을 확인하시기 바랍니다.)
- 0.1
- 0.56
- 0.7
- 56
10. 꼭지각이 30°인 프리즘의 굴절률은 파란색 광선에 대해서 1.65이고, 빨간색 광선에 대해서 1.61이라면 두 파장 범위 내에서 각분산(angular dispersion)은?
- 1.31°
- 2.62°
- 3.38°
- 4.18°
11. 그림과 같이 원래의 상이 찌그러진 상으로 나타내는 이유는 어떤 현상 때문인가?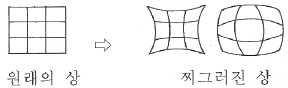
- 코마
- 구면수차
- 왜곡수차
- 비점수차
12. 광학 유리에 대하여 가시광 영역에서 다음 내용 중 옳은 것끼리 짝지어진 것은?
- A, C
- A, D
- B, C
- B, D
13. 그림과 같이 포로프리즘(Porro prism)을 2장 겹쳐 놓고서 물체의 위치에 R을 놓았다. R은 어떻게 보이는가?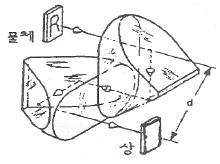
- R
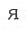

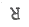
14. 볼록렌즈 앞 50cm되는 곳에 점광원이 있다. 이때의 상이 맺히는 거리는 렌즈에 평행광선이 입사되었을 때 상거리의 5배가 되었다면 이 렌즈의 초점거리는?
- 10cm
- 20cm
- 30cm
- 40cm
15. 초점거리가 10cm인 렌즈의 오른쪽 5cm떨어진 지점에 직경 2cm인 구경 조리개가 있다. 입사동의 크기는 몇 cm 인가?
- 1
- 2
- 4
- 8
16. He-Ne 레이저에서 발생한 평행광선이 광축을 따라서 단일 볼록렌즈에 의해 접속될 때, 초점에 한 점으로 모이지 않고 크기를 갖는 원으로 모이는 것은 무슨 수차 때문인가?
- 구면수차
- 코마수차
- 왜곡수차
- 상면만곡수차
17. 천체망원경 대물렌즈의 초점거리가 40cm, f수가 5이다. 평행한 광선이 들어오고 바깥쪽 눈동자의 직경이 2cm일 때 접안렌즈의 초점거리와 망원경의 배율을 구하면?
- 2cm, 1배
- 5cm, 2배
- 8cm, 3배
- 10cm, 4배
18. 핀홀 카메라의 왼쪽에 물체가 놓여 있고 이 물체로부터 오른쪽으로 3m 떨어진 곳에 물체 크기의 1/5이 되는 상이 맺혔다. 핀홀과 상까지의 거리는 얼마인가?
- 15cm
- 30cm
- 50cm
- 60cm
19. 다음 중 구경 조리개(Aperture stop)의 크기에 가장 크게 의존하는 수차는?
- 구면수차
- 코마수차
- 만곡수차
- 왜곡수차
20. 두꺼운 양면 볼록렌즈의 곡률반경이 각각 8cm, -8cm이고 가운데 두께가 1cm, 굴절률이 1.6일 때 이 렌즈계의 초점거리는 약 얼마인가?
- 3.3cm
- 4.2cm
- 5.2cm
- 6.8cm
2과목: 파동광학
21. 영(Young)의 이중 슬릿 실험에서 얻어지는 간섭무늬의 간격은 슬릿 간격과 슬릿과 스크린 사이의 거리, 그리고 사용하는 빛의 파장에 의해서 결정된다. 다음 중 간섭무늬의 간격을 줄일 수 있는 경우는?
- 슬릿 간격을 넓힌다.
- 슬릿과 스크린 사이의 거리를 넓힌다.
- 파장이 큰 빛을 사용한다.
- 간격을 줄일 수 없다.
22. 핫 미러(hot mirror)에 대한 설명으로 옳은 것은?
- 어떤 특정한 파장을 반사시키고, 나머지 파장들은 투과시킨다.
- 적외선을 반사시키고, 가시광선을 투과시킨다.
- 적외선을 투과시키고, 가시광선을 반사시킨다.
- 스펙트럼에서 파장의 일부 영역만 차단시킨다.
23. 그림은 광섬유 측단면을 나타낸 것이다. 허용각(acceptance angle) α를 표현한 것으로 옳은 것은? (단, 코어와 클래딩의 굴절률은 각각 n1, n2 이며, 공기의 굴절률 n0는 1이다.)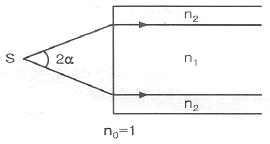
24. 굴절률이 n인 매질 내에서 빛이 진행하는 속도는? (단, 진공 중의 빛의 속도는 c이다.)
- cㆍn
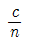
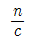
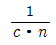
25. 폭이 1인 1차원 사각함수(rectangular function)에 대한 푸리에(Fourier) 변환 함수는? (단, fx는 공간주파수(spatial frequency)이다.)
- exp(-πf2x)
- δ(fx)

- cos(πfx)
26. 광학 부품 중 공간주파수 분석기의 역할을 하는 대표적인 것은?
- 렌즈
- 레이저
- 프리즘
- 평면거울
27. 방해석에게 광축에 수직인 방향으로 진행하는 빛에 대한 설명으로 옳은 것은?
- 이상광선과 정상광선의 구별이 없다.
- 이상광선이 정상광선보다 느리게 진행한다.
- 이상광선이 정상광선보다 빠르게 진행한다.
- 이상광선과 정상광선이 같은 속도로 진행한다.
28. 초점거리 20cm인 볼록렌즈의 한 초평면 상에 폭 1㎛의 슬릿을 위치시킨 후, 500nm 파장의 광을 슬릿에 수직 입사하여 렌즈의 반대편 초평면 상에 나타나는 회절무늬를 관찰한다. 1차 어두운 회절무늬의 위치는 무늬의 중심에서 얼마의 거리에 있는가?
- 1cm
- 5cm
- 10cm
- 20cm
29. Na(소디움, sodium) 이중선(λ1=5895.9°Å, λ2=5890.0Å)을 삼차 회절광에서 분리시키기 위하여서는 격자의 총 격자선이 몇 줄이어야 되는가?
- 333
- 500
- 999
- 1964
30. 굴절률이 n1인 기판 위에 두께가 λ/4인 1층 박막을 증착하여 무반사막을 만들려고 한다. 증착물질의 굴절률을 nT라고 할 때 n1값이 얼마이어야 무반사 조건이 만족되겠는가?
- n1=√nT
- n1=3√nT
- n1=nT2
- n1=nT3
31. 광통신에 주로 사용되는 C-band의 파장 영역은?
- 800~900nm
- 1260~1360nm
- 1365~1525nm
- 1530~1562nm
32. 굴절률 n1=1.66인 core와 n2=1.52인 cladding으로 이루어진 직선 광섬유에 대해 최대입사 허용각(acceptance angle)θ1은 얼마인가?
- 66°
- 55°
- 24°
- 42°
33. 두 개의 론키 격자(Ronchi rulings)를 겹치면 무아레 무늬를 관찰할 수 있다. 이 무늬에 대한 설명으로 틀린 것은?
- 백색광에서도 무늬를 볼 수 있다.
- 격자면의 변형을 측정할 수 있다.
- 유리의 공간적 굴절률 변화율을 알 수 있다.
- 격자를 회전시키면 무늬 간격이 변화한다.
34. 굴절률 ni인 매질에서 굴절률 nt(<ni)인 매질로 빛이 입사할 때 전반사가 일어나는 임계각 θc에 대한 표현 중 옳은 것은?
35. 다음 중 홀로그램의 특성이 아닌 것은?
- 기준파의 위치가 변하면 상의 크기는 변하지 않으나, 상의 위치는 변화한다.
- 홀로그램을 작은 조각으로 잘라내어도, 각 조각은 물체의 온전한 상을 모두 포함한다.
- 제작된 홀로그램을 밀착 인화(contact printing)하면 동일한 성질의 또 다른 홀로그램을 만들 수 있다.
- 기록광 파장의 2배 파장을 갖는 광으로 홀로그램을 재생할 때, 재생된 상의 횡배율이 2배이면 종배율도 2배이다.
36. 다음 맥스웰(Maxwell) 방정식 중 패러데이(Faraday) 법칙과 관련된 것은?
37. 그림과 같이 평면유리 위에 plano-convex lens를 올려놓고 위에서 λ의 파장을 갖는 광을 쬐여 준다. 이때 형성되는 간섭무늬를 Nextons ring이라 한다. 간섭무늬의 첫 번째 어두운 부분까지의 반경이 1mm라면 사용된 광원의 파장은? (단, plano-convex lens의 곡률반경은 4m이다.)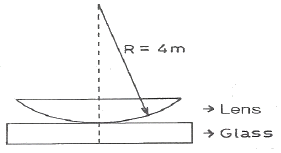
- 250nm
- 450nm
- 500nm
- 550nm
38. 파장이 1.5㎛이고 빔의 직경이 1mm인 가우스 광속을 렌즈에 입사시켜 지름이 10㎛인 광섬유 코어에 집속시키려고 하면, 필요한 렌즈의 초점거리는 약 몇 mm인가?
- 4.8
- 5.2
- 5.7
- 6.3
39. 다음 중 광섬유의 손실 원인이 아닌 것은?
- 레일리 산란
- OH 이온들의 진동에 의한 흡수
- 미세 휨 손실
- 실리카에 의한 흡수
40. 파장 500nm의 단색광을 이용하는 마이캘슨 간섭계가 있다. 간섭계의 한 쪽 팔에 굴절률이 1.5이고 두께가 40㎛인 유리판을 삽입할 때, 간섭무늬의 이동(displacement) 개수는 몇 개인가?
- 20개
- 40개
- 80개
- 120개
3과목: 광학계측과 광학평가
41. 다음 중 조리개를 중심으로 같은 형태의 렌즈가 서로 마주보고 있는 (대칭)렌즈계는?
- Double Gauss
- Petzval lens
- Cooke Triplet
- Tessar
42. 프리즘의 종류를 사용하는 기능으로 분류할 때 포함되지 않는 것은?
- 편광 프리즘
- 반사 프리즘
- 분산 프리즘
- 위상 프리즘
43. 카메라의 렌즈에는 무반사 코팅을 하여 피사체로부터 오는 빛의 반사를 막는다. 렌즈의 굴절률을 1.5, 코팅 재료의 굴절률을 1.3이라 하고, 가시광선의 중간 파장인 550nm에 대해 수직입사 시 무반사 코팅을 하고자 하면 코팅 막의 최소 두께는 약 얼마인가?
- 92nm
- 106nm
- 184nm
- 212nm
44. 다음 중 레이저가 결정에 입사된 후 파장이 변화하여 산란되는 현상을 나타내는 것은?
- 라만(Raman) 효과
- 레일리(Rayleigh) 효과
- 뫼스바우어(Mossbauer) 효과
- 제만(Zeeman) 효과
45. 그림을 임상현미경용 대물렌즈이다. 그림에 대한 설명 중 틀린 것은?
- 170은 경통 길이이다.
- PL은 Plane lens를 뜻한다.
- 100은 100X 배율이다.
- 1.32는 초점거리이다.
46. 광학 유리의 중요한 특징 중 하나는 파장에 따른 빛의 투과성(Transmittance)이다. CO2레이저의 경우 파장이 10.6㎛로 보편적으로 사용되는 광학유리는 사용할 수 없다. 다음 중 CO2레이저의 파장영역에서 사용 가능한 광학물질은?
- 실리콘
- 사파이어
- 실리카
- 셀렌화 아연(ZnSe)
47. 최근 광통신분야에 널리 사용되고 있는 광섬유의 장점을 전기도체와 비교하여 설명한 것 중 틀린 것은?
- 무게가 가볍고 비용이 저렴하다.
- 좁은 대역폭을 가지고 있다.
- 전기적 간섭을 일으키지 않는다.
- 많은 양의 신호운반이 가능하다.
48. 다음 중 바늘구멍 사진기에 대한 설명으로 옳은 것은?
- 초점 심도가 깊다.
- 시야가 좁다.
- 상이 왜곡된다.
- 노출 시간이 짧다.
49. 디지털 표시장치나 디스플레이 등에 많이 사용되는 액정(liquid crystal)의 광학 특성에 대한 설명으로 옳은 것은?
- 액정의 굴절률 차이를 이용한다.
- 액정 주위에 있는 편광기를 돌린다.
- 액정에 가해진 전압에 따른 편광 투과 특성을 이용한다.
- 액정 자체에서 나오는 발광 특성을 이용한다.
50. 렌즈의 굴절능이 1Diopter로 주어졌다. 렌즈의 초점거리를 분모로 쓸 때 이 관계를 나타낸 것은?
- 1/1mm
- 1/1cm
- 1/1m
- 1/1km
51. 간격이 d인 회절격자에 입사각 i로 파장 λ의 빛을 평행하게 입사시켰을 때 θ의 각으로 회절 되었다. 이때 principal maxima가 일어나려면 조건 m이 임의의 정수일 때 어떻게 되는가?
- dㆍsin i = mλ
- dㆍsin θ = mλ
- d(sin i + sin θ) = mλ
- dㆍsin(i+θ) = mλ
52. 초점거리가 50cm, Abbe 수가 44인 렌즈와 다른 렌즈를 접착하여 색수차 보정렌즈(Achromat condition)를 구성하고자 할 때 다른 렌즈의 초점거리가 –40cm이면 이 렌즈의 유리로 적합한 것은?
- md=1.574, vd=57.7
- md=1.617,d=55.0
- md=1.584, vd=46.0
- md=1.573, vd=42.5
53. λ1=589nm와 λ2=589.6nm의 두 선으로 구성되어 있는 나트륨 D선을 어떤 회절격자를 이용하여 분해하고자 한다. 유용한 슬릿의 수가 500개이면, 이 두 선이 분해되는 가장 낮은 차수는?
- 1
- 2
- 3
- 4
54. 어떤 렌즈 앞 20cm 되는 곳에 물체를 놓으니 2배의 실상이 나타났다면 렌즈 종류와 초점거리는?
- 볼록렌즈, 13.3cm
- 오목렌즈, -13.3cm
- 볼록렌즈, 40cm
- 오목렌즈, -40cm
55. 얇은 Ge(굴절률=4.0)판을 공기 중에서 적외선 광학기기의 창(window)으로 사용하려고 한다. 반사율을 파장 8000nm에서 0%로 하기 위해 단층박막을 1/4 파장 두께로 코팅하려고 한다. 단층박막의 두께는 얼마이어야 하는가? (단, 코팅 박막의 굴절률은 2.0이다.)
- 100nm
- 500nm
- 800nm
- 1000nm
56. 일반적인 광학유리의 구성 원소 중 가장 많이 포함되는 것은?
- Al2O3
- SiO2
- Na2O
- B2O3
57. 대물렌즈의 초점거리가 500mm, 접안렌즈의 초점거리가 20mm인 천체 망원경의 배율은 몇 배인가?
- 10배
- 15배
- 25배
- 50배
58. 다음 광학재료 중 가장 표면손상을 입기 쉽고 내마모성이 떨어지는 재료는?
- PC
- PMMA
- CR-39
- 유리
59. 에돌이발(diffraction grating, 회절격자)에 대한 설명 중 틀린 것은?
- 빛의 회절 특성을 이용한다.
- 두 경로를 지나는 빛 사이의 위상차로 생기는 간섭 효과를 이용한다.
- 쪼여지는 빛을 파장별로 분리할 수 있다.
- 물체에서 반사하는 빛의 반사율을 측정하는 광학 소자이다.
60. 급커브의 도로상에는 볼록거울을 설치하여 운전자의 전방 광찰을 용이하게 도와준다. 볼록거울을 설치하는 이유는?
- 물체거리에 관계 없이 도립실상을 맺는다.
- 물체거리에 따라 확대된 직립허상을 맺는다.
- 물체거리에 관계 없이 축소된 직립허상을 맺는다.
- 물체거리에 따라 허상 또는 실상을 맺는다.
4과목: 레이저 및 광전자
61. 동일 파장의 두 개의 Coherent한 레이저 빔이 각도 α로 교차할 때 그 교차점에 생기는 간섭무늬의 간격은 얼마인가? (단, 레이저 빔의 파장은 λ이다.)
62. 레이저 광원에서 나온 두 개의 레이저 빔을 간섭시켜 사진필름에 기록하면 간섭무늬를 얻을 수 있다. 간섭무늬의 간격을 결정하는 주된 요소는 무엇인가?
- 필름의 굴절률
- 레이저의 파장
- 레이저의 스팟 크기
- 레이저의 결맞음 거리
63. 파장 500nm의 이상적인 레이저 광속을 그림과 같이 집속하였을 때, 발산각 θ가 1mrad이었다. 빔 허리(Beam waist)의 반지름 Wo는 약 얼마인가?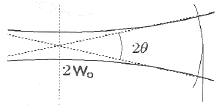
- 79.6㎛
- 122.0㎛
- 159.2㎛
- 305.3㎛
64. 선폭이 △v=3×102Hz 인 레이저광의 가간섭시간(결맞음 시간)은?
- 3.3×10-6초
- 2.2×10-4초
- 3.3×10-3초
- 2.2×10-3초
65. 편광을 얻을 수 없는 것은?
- 복굴절을 이용하여 얻을 수 있다.
- 이색성 결정체에 의해 얻을 수 있다.
- 프리즘 막대를 통과시켜서 얻을 수 있다.
- 특별한 입사각(편광각)으로 입사시켜 반사된 빛에 의해 얻을 수 있다.
66. 편광자와 검광자의 편광 방향을 나란하게 겹쳐 놓고 햇빛에 비치면 밝게 보일 때 그 사이에 매우 얇은 Waxed paper를 끼우면 어둡게 변하는 이유는?
- Wax 분자에서 굴절효과 때문
- Waxed paper 때문에 빛이 간섭을 일으켜서
- Waxed paper 때문에 복굴절이 일어나기 때문에
- Waxed paper에 의해 산란된 빛이 편광되기 때문에
67. 전기방전으로 여기될 수 없는 레이저는?
- CO2 레이저
- 색중심 레이저
- Ar+ 레이저
- 구리 증기 레이저
68. 홀로그래피에 이용하는 Ar레이저에 에탈론(etalon)을 사용하는 이유는?
- 출력의 안정을 가하기 위하여
- 횡모드 특성을 좋게 하기 위하여
- 공간적 결맞음(spatial coherence)을 늘리기 위하여
- 시간적 결맞음(temporal coherence)을 늘리기 위하여
69. 레이저 다이오드의 20GHz/℃의 온도 의존도를 갖는다고 가정할 때, 주파수의 변화가 100MHz이하가 되게 하려면 허용 가능한 온도 변화는 얼마인가?
- 0.005℃
- 0.25℃
- 0.025℃
- 0.5℃
70. 레이저를 이용한 홀로그래피는 레이저 빛의 어떤 성질을 이용한 것인가?
- 간섭성
- 고휘도성
- 직진성
- 고집속성
71. 어떤 결정체의 유전율 텐서(tensor)가 직각좌표계로 다음과 같이 표현된다. X 축 방향으로 편광된 빛이 Z축 방향으로 진행할 때 빛의 결정 내 진행속도가 2×108m/s이라면 Z축 방향으로 편광된 빛이 X축으로 진행하는 결정 내 속도는 얼마인가?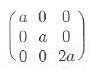
- 1×108m/sec
- √2×108m/sec
- 2×108m/sec
72. 광축과 45°방향으로 선형 – 편광된 빛이 λ/4판(quarter-wave plate)을 통과하여 나오는 편광 상태는?
- 타원 편광
- 45°선형 편광
- 원형 편광
- 90°선형 편광
73. 편광되지 않은 빛이 입사할 때 그림과 같이 대칭으로 진행하는 수직한 선편광으로 분리하는 프리즘의 명칭은?
- Wollaston
- Rochon
- Sernamont
- Glan-Thompson
74. 전기장이 선형 편광자를 지난 후 E(z,t)=1.5 cos(ωt-kz)j가 된다. 45°로 y축에 대해 놓여 있는 또 다른 선형 편광자를 지날 때 빛의 세기는 첫 번쨰 편광자를 지난 후와 비교하면 얼마나 줄어드는가?
- 1/8
- 1/6
- 1/4
- 1/2
75. 전기장 E1=cos(ø1)+isin(ø1), E2=cos(ø2(V))+isin(ø2(V))일 때 두 전기장의 간섭 세기 표현식은?
- 2(1+sin(ø2(V)-ø1))
- 2(1+sin(ø2(V)+ø1))
- 2(1+cos(ø2(V)-ø1))
- 2(1+cos(ø2(V)+ø1))
76. 다음 중 굴절률 정합 방법이 아닌 것은?
- LiNbO3는 굴절률이 온도의 분산함수로 변하므로 적당한 온도에서
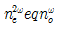 가 될 수 있다.
가 될 수 있다. - 각각의 파장이 λ1, λ2인 광이 진행하여 λ3인 광이 방출되며 이들이 같은 방향으로 진행할 경우 λ1+λ2=λ3가 된다.
- KDP type I의 경우 결정축을 회전하여 적당한 전파방향과 이루는 각도 θm에 대해서
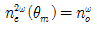 가 되게 한다.
가 되게 한다. - 정상광선 축과 이상광선 축으로 각각 ω의 광을 입사시켜 이상광선 축에서 2ω의 광을 발생시키는 KDP type ∥의 경우
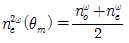 로 한다.
로 한다.
77. 레이저 광의 일반적인 특성으로 틀린 것은?
- 진동수가 매우 일정한 광파이다.
- 스펙트럼 폭이 아주 작은 단색광이다.
- 레이저 광은 거의 퍼지지 않는 상태로 직진한다.
- 레이저 광은 간섭현상이 나타나지 않는 광파이다.
78. 단축 결정체(uniaxial crystal)에서 입사광의 전파방향이 광축과 몇 도 각도를 이룰 때 복굴절 현상이 보이지 않는가?
- 0°
- 30°
- 45°
- 60°
79. 광 리소그라피에서 초미세 형상의 노광에 가장 적합한 레이저는?
- He-Ne 레이저
- 구리 증기 레이저
- Nd:YAG 레이저
- ArF 엑시머 레이저
80. 파장 가변레이저라고 할 수 없는 것은?
- KrF 레이저
- 자유전자 레이저
- Dye 레이저
- Ti:Al2O3 레이저






 "로 보입니다.
"로 보입니다.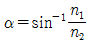
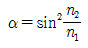
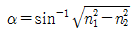

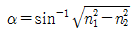 " 이다.
" 이다.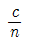 "이다.
"이다. "이다.
"이다.

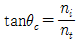
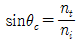
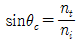 "이다. 이유는 굴절률이 작은 매질에서 굴절률이 큰 매질로 빛이 입사할 때, 임계각 이상으로 입사하면 전반사가 일어나기 때문이다. 이때 임계각 θc는 아래와 같이 표현된다.
"이다. 이유는 굴절률이 작은 매질에서 굴절률이 큰 매질로 빛이 입사할 때, 임계각 이상으로 입사하면 전반사가 일어나기 때문이다. 이때 임계각 θc는 아래와 같이 표현된다.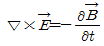
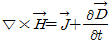
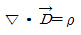
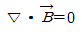
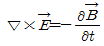 "이다. 이는 패러데이 법칙으로, 전자기장의 변화가 자기장을 유도하는 것을 나타낸다. 이 식은 전자기학에서 가장 기본적인 법칙 중 하나이며, 전자기장의 원리를 이해하는 데 매우 중요하다.
"이다. 이는 패러데이 법칙으로, 전자기장의 변화가 자기장을 유도하는 것을 나타낸다. 이 식은 전자기학에서 가장 기본적인 법칙 중 하나이며, 전자기장의 원리를 이해하는 데 매우 중요하다.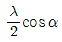
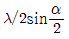
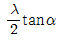
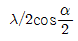
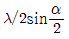 "이다.
"이다.