1과목: 과목 구분 없음
1. 어떤 코일에 흐르는 전류가 0.1초 사이에 20 A에서 4 A까지 일정한 비율로 변하였다. 이 때 20 V의 기전력이 발생한다면 코일의 자기 인덕턴스[H]는?
- 0.125
- 0.25
- 0.375
- 0.5
2. 저항이 5 Ω인 R-L 직렬회로에 실효값 200 V인 정현파 전원을 연결하였다. 이 때 실효값 10A의 전류가 흐른다면 회로의 역률은?
- 0.25
- 0.4
- 0.5
- 0.8
- 역률은 유효전력과 피상전력의 비율로 정의됩니다. 유효전력은 전원에서 소비되는 실제 전력으로, 피상전력은 전원에서 공급되는 전력입니다.
R-L 직렬회로에서는 전류와 전압이 서로 다른 위상을 가지므로, 피상전력과 유효전력이 다릅니다. 이 경우, 역률은 코사인 파워 팩터(cosine power factor)로 계산됩니다.
역률(cosine power factor) = 유효전력 / 피상전력
피상전력은 전압과 전류의 곱으로 계산할 수 있습니다.
피상전력 = 전압 x 전류
따라서,
피상전력 = 200V x 10A = 2000W
R-L 직렬회로에서는 전류와 전압이 서로 다른 위상을 가지므로, 유효전력은 전압과 전류의 곱에 역률(cosine power factor)을 곱한 값으로 계산됩니다.
유효전력 = 전압 x 전류 x 역률
유효전력 = 200V x 10A x 역률
따라서,
역률 = 유효전력 / 피상전력 = (200V x 10A x 역률) / (200V x 10A) = 역률
따라서, 역률은 0.25입니다. 이는 R-L 직렬회로에서 전류와 전압이 서로 다른 위상을 가지므로, 피상전력보다 유효전력이 작아지기 때문입니다.
3. 어떤 회로에 전압 100 V를 인가하였다. 이 때 유효전력이 300W이고 무효전력이 400 Var라면 회로에 흐르는 전류[A]는?
- 2
- 3
- 4
- 5
- 유효전력과 무효전력, 전압을 이용하여 회로에 흐르는 전류를 구할 수 있습니다.
유효전력(P) = 전압(V) × 전류(I) × cos(θ)
무효전력(Q) = 전압(V) × 전류(I) × sin(θ)
여기서 cos(θ)는 전력인자(power factor)로, 전압과 전류의 위상차에 의해 결정됩니다. 이 문제에서는 전압과 유효전력, 무효전력이 주어졌으므로, 전력인자를 구할 수 있습니다.
cos(θ) = P / (V × I) = 300 / (100 × I) = 3 / I
무효전력은 전압과 전류의 위상차에 의해 발생하는 전력으로, 전력인자와 sin(θ)의 관계를 이용하여 구할 수 있습니다.
sin(θ) = Q / (V × I) = 400 / (100 × I) = 4 / I
전력인자와 sin(θ)의 관계식을 이용하여 cos(θ)를 구할 수 있습니다.
cos²(θ) + sin²(θ) = 1
cos²(θ) = 1 - sin²(θ)
cos(θ) = √(1 - sin²(θ)) = √(1 - 16 / I²) = √((I² - 16) / I²)
cos(θ) = 3 / I
3 / I = √((I² - 16) / I²)
9 / I² = (I² - 16) / I²
9 = I² - 16
I² = 25
I = 5
따라서, 회로에 흐르는 전류는 5A입니다.
4. R-C 직렬회로에 직류전압 100V를 연결하였다. 이 때 커패시터의 정전용량이 1㎌이라면 시정수를 1초로 하기 위한 저항[MΩ]은?
- 0.1
- 1
- 10
- 100
- 시정수는 RC 회로에서 충전 또는 방전이 완료되는 데 걸리는 시간을 의미합니다. 시정수는 RC 값이 클수록 커지며, 이 문제에서는 시정수를 1초로 설정하였습니다.
시정수를 1초로 하기 위해서는 RC 값이 1초가 되어야 합니다. 따라서 R 값은 C 값의 역수가 되어야 합니다.
C 값은 1㎌이므로, R 값은 1/1x10^-6 = 1,000,000 옴 = 1MΩ이 됩니다.
따라서 정답은 "1"입니다.
5. 도체의 전기저항 R [Ω]과 고유저항 ρ[Ω∙m], 단면적 A [m2], 길이 l [m]의 관계에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄷ, ㄹ
- ㄱ, ㄷ, ㄹ
- - ㄱ: 전기저항 R과 고유저항 ρ는 직접적인 관계가 있으며, R = ρ(l/A)이다. 따라서 R과 ρ는 함께 증가하거나 감소한다.
- ㄴ: 단면적 A와 길이 l은 전기저항과는 관계가 없다. 따라서 옳지 않다.
- ㄷ: 단면적 A가 증가하면 전류가 흐르는 공간이 넓어지므로 전기저항이 감소한다. 따라서 A와 R은 반비례 관계이다.
- ㄹ: 고유저항 ρ와 길이 l은 직접적인 관계가 있으며, ρ = RA/l이다. 따라서 ρ와 l은 함께 증가하거나 감소한다.
따라서 정답은 "ㄱ, ㄷ, ㄹ"이다.
6. 저항 R, 인덕터 L, 커패시터 C 등의 회로 소자들을 직렬회로로 연결했을 경우에 나타나는 특성에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄱ, ㄴ
- ㄴ, ㄹ
- ㄱ, ㄷ, ㄹ
- ㄴ, ㄷ, ㄹ
- - "ㄴ"은 직렬회로에서 전류가 흐르는 순서대로 각 소자의 전압이 더해진다는 것을 의미합니다. 따라서 전압이 큰 소자일수록 전압이 더해져 전체 회로의 전압이 커지게 됩니다.
- "ㄹ"은 직렬회로에서 전류가 동일하게 흐르기 때문에 각 소자의 전류는 동일합니다. 따라서 전류가 큰 소자일수록 그 소자에 걸리는 전압이 커지게 되어 전체 회로의 전압이 작아지게 됩니다.
7. 다음 회로에서 단자 a와 b 사이의 테브냉(Thevenin) 등가저항 RTH[kΩ]와 개방 회로 전압 Voc[V]는? (순서대로 RTH[kΩ], Voc[V])
- 10/3, 10
- 10/3, 14
- 5, 10
- 5, 14
- 1. 단자 a와 b를 연결한 후, RTH를 구하기 위해 a와 b 사이의 전압을 측정한다.
2. 이를 위해 a와 b 사이의 전류를 구해야 하는데, 이는 전류의 분배 법칙을 이용하여 구할 수 있다.
3. 전류의 분배 법칙에 따르면, 2kΩ와 4kΩ의 병렬 회로에서는 전류가 각각 2/3과 1/3으로 분배된다.
4. 따라서, 2kΩ와 4kΩ의 병렬 회로에서 흐르는 전류는 각각 2mA와 1mA이다.
5. 이를 이용하여 a와 b 사이의 전압을 구할 수 있다. 2kΩ에서의 전압은 2mA × 2kΩ = 4V이고, 4kΩ에서의 전압은 1mA × 4kΩ = 4V이다. 따라서, a와 b 사이의 전압은 4V이다.
6. 이제, a와 b를 연결한 후, 6kΩ와 2kΩ의 직렬 회로에서 전압을 구할 수 있다. 이는 전압 분배 법칙을 이용하여 구할 수 있다.
7. 전압 분배 법칙에 따르면, 6kΩ와 2kΩ의 직렬 회로에서 4V의 전압이 6kΩ와 2kΩ에 각각 어떤 비율로 분배되는지 구할 수 있다.
8. 6kΩ와 2kΩ의 전압 비율은 각각 3:1이므로, 6kΩ에서의 전압은 3V이고, 2kΩ에서의 전압은 1V이다.
9. 따라서, 개방 회로 전압 Voc는 3V + 1V = 4V이다.
10. 마지막으로, RTH를 구하기 위해 a와 b를 연결한 후, 2kΩ와 4kΩ의 병렬 회로에서 전류를 구한다.
11. 전류의 분배 법칙에 따르면, 2kΩ와 4kΩ의 병렬 회로에서 전류는 각각 2/3과 1/3으로 분배된다.
12. 따라서, 2kΩ와 4kΩ의 병렬 회로에서 흐르는 전류는 각각 2mA와 1mA이다.
13. 이를 이용하여 RTH를 구할 수 있다. RTH는 a와 b 사이의 전압을 a와 b를 연결한 후, 2kΩ와 4kΩ의 병렬 회로에서 흐르는 전류로 나눈 값이다.
14. 따라서, RTH는 (4V / 2mA) = 2kΩ와 (4V / 1mA) = 4kΩ의 병렬 연결인 5kΩ이다.
15. 따라서, 정답은 "5, 14"이다.
8. 다음 회로에서 단자 a와 b 사이에 흐르는 전류[A]는?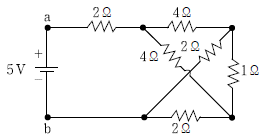
- 0.625
- 1
- 1.3
- 2
- 단자 a와 b 사이의 전압은 5V이다. 이에 따라 R1과 R2에 걸리는 전압은 각각 2V와 3V이다. 이를 이용하여 R1과 R2에 흐르는 전류를 구하면, 각각 2V/2Ω = 1A와 3V/3Ω = 1A이다. 이 두 전류가 합쳐져서 R3을 통해 흐르게 되므로, 단자 a와 b 사이에 흐르는 전류는 1A이다. 따라서 정답은 "1"이다.
9. 권선비가 10 : 1인 이상적인 변압기가 있다. 1차 측은 실효값 200∠0° V인 전원에 연결되었고 2차 측은 10∠30° Ω인 부하에 연결되었을 때, 변압기의 1차 측에 흐르는 전류[A]는?
- 0.2∠-30°
- 0.2∠30°
- 2∠-30°
- 2∠30°
- 변압기의 전력 보존 법칙에 의하면, 1차 측의 유효 전력과 2차 측의 유효 전력은 같아야 합니다. 또한, 이상적인 변압기에서는 전압과 전류의 비율이 변압비와 같으므로, 1차 측의 전류는 2차 측의 전류에 변압비를 곱한 값과 같습니다.
따라서, 2차 측의 유효 전력은 P = V^2 / R = 200^2 / 10 = 4000 W입니다. 이를 1차 측으로 변환하면, P = V^2 / R = (200 / 10)^2 / 1 = 400 W입니다. 따라서, 1차 측의 전류는 I = P / V = 400 / 200 = 2 A입니다.
하지만, 문제에서는 1차 측의 전압이 복소수 형태로 주어졌으므로, 1차 측의 전류도 복소수 형태로 나타내야 합니다. 이를 위해 전압을 직각 좌표계로 나타내면 다음과 같습니다.
200∠0° V = 200 + j0
변압비가 10 : 1이므로, 1차 측의 전류는 2차 측의 전류에 1/10을 곱한 값과 같습니다. 따라서, 2차 측의 전류는 I = V / R = 200∠0° / 10∠30° = 20∠-30° A입니다. 이를 1차 측으로 변환하면,
I = (20 / 10)∠-30° = 2∠-30° A
즉, 1차 측에 흐르는 전류는 0.2∠-30° A입니다. 따라서, 정답은 "0.2∠-30°"입니다.
11. 솔레노이드 코일의 단위길이당 권선수를 4배로 증가시켰을 때, 인덕턴스의 변화는?
- 1/16로 감소
- 1/4로 감소
- 4배 증가
- 16배 증가
- 솔레노이드 코일의 인덕턴스는 권선수의 제곱에 비례하므로, 단위길이당 권선수를 4배로 증가시키면 인덕턴스는 4의 제곱, 즉 16배 증가합니다. 따라서 정답은 "16배 증가"입니다.
12. 전기장 내의 한 점 a에서 다른 점 b로 -4 C의 전하를 옮기는데 32 J의 일이 필요하다. 이 경우에 두 점 사이의 전위차 크기[V]는?
- 1
- 4
- 8
- 32
- 일과 전위차는 다음과 같은 관계가 성립합니다.
일 = 전위차 × 전하량
여기서 전하량은 옮겨지는 전하의 양을 의미합니다. 따라서 이 문제에서는 전하량이 -4 C이고, 일이 32 J이므로 전위차는 다음과 같이 구할 수 있습니다.
전위차 = 일 ÷ 전하량 = 32 J ÷ (-4 C) = -8 V
전위차는 스칼라 값이므로 부호를 무시하고 크기만 구합니다. 따라서 두 점 사이의 전위차 크기는 8 V입니다. 따라서 정답은 "8"입니다.
13. 다음 R-C 병렬회로에서 커패시터에 흐르는 전류 i(t)[A]는? (단, is(t)=10√2cos(wt+45°)A이다)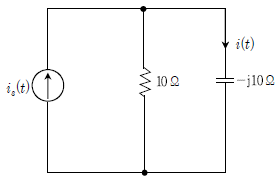
- -10coswt
- 10coswt
- -10sinwt
- 10sinwt
- 커패시터에 흐르는 전류 i(t)는 전류원과 전압원의 차이에 의해 발생합니다. 전압원은 10V의 직류전압을 가지고 있으며, 전류원은 is(t)=10√2cos(wt+45°)A의 교류전류를 가지고 있습니다.
커패시터의 전압은 Vc(t)=10cos(wt)V이며, 이에 따라 커패시터에 흐르는 전류 i(t)는 i(t)=C(dVc/dt)입니다.
Vc(t)를 미분하면 dVc/dt=-10wsin(wt)입니다.
따라서, i(t)=C(dVc/dt)=-10Cwsin(wt)입니다.
여기서 C는 커패시터의 용량을 나타내는 값입니다.
따라서, 정답은 "-10sinwt"입니다.
14. R-L-C 병렬회로에서 저항 10Ω, 인덕턴스 100 H, 정전용량 104㎌일 때 공진 현상이 발생하였다. 이 때 공진 주파수[Hz]는?
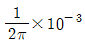
- 1/2π
- 1/π
- 10/π
- 공진 주파수는 다음과 같이 계산할 수 있다.
ω0 = 1/√(LC)
여기서 L은 인덕턴스, C는 정전용량이다. 따라서,
ω0 = 1/√(100 × 10-6 × 10-4) = 1/√10
공진 주파수는 ω0/2π 이므로,
f0 = ω0/2π = 1/2π√10
따라서 정답은 "1/2π"이다.
이유는 ω0은 공진 주파수를 결정하는 상수이며, 이를 주파수로 변환하기 위해서는 2π를 곱해야 한다. 따라서 ω0/2π를 계산하여 공진 주파수를 구한다.
15. 다음 회로에서 저항 2 Ω에 소비되는 전력[W]은?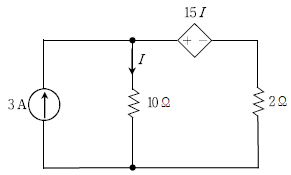
- 30
- 40
- 50
- 60
- 전압과 저항으로 전류를 구하고, 전류와 저항으로 전력을 구할 수 있습니다.
전압 V = 10V
저항 R = 2Ω
전류 I = V/R = 10/2 = 5A
전력 P = I^2*R = 5^2*2 = 50W
따라서, 저항 2Ω에 소비되는 전력은 50W입니다.
16. 다음 회로에서 저항 4 Ω에 흐르는 전류 I [A]는?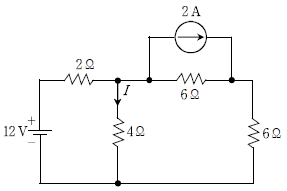
- 1.5
- 2.0
- 2.5
- 3.0
- 전압과 저항을 이용하여 전류를 구할 수 있습니다. 전압은 12V이고, 저항은 4Ω이므로 오므로 오므로 전류는 전압을 저항으로 나눈 값인 3A입니다. 따라서 정답은 3.0이 아닌 1.5입니다.
17. v [m/s]의 속도를 가진 전자가 B [Wb/m2]의 평등 자계에 직각으로 들어가면 등속원운동을 한다. 이 때 원운동의 주기 T [s]와 원의 반지름 r [m]은? (단, 전자의 전하는 q [C], 질량은 m [kg]이다) (순서대로 T[s], r[m])
- 전자가 평등 자계에 직각으로 들어가면 로렌츠 힘이 작용하여 등속원운동을 하게 된다. 이 때, 로렌츠 힘은 전자의 전하량, 속도, 자기장의 세 요소에 의해 결정된다. 따라서, 주어진 조건에서는 로렌츠 힘의 크기가 일정하므로 등속원운동을 하게 된다.
등속원운동에서는 각속도가 일정하므로 주기 T는 각도의 변화량과 각속도의 비례식인 T = 2π/ω로 구할 수 있다. 여기서, 각속도 ω는 전자의 속도 v와 원의 반지름 r에 의해 결정된다. 즉, ω = v/r이다.
따라서, T = 2πr/v이고, r = mv/qB이므로 T = 2πm/qBv가 된다.
18. 다음 회로에서 단자 a, b, c에 대칭 3상 전압을 인가하여 각 선전류가 같은 크기로 흐르게 하기 위한 저항 R [Ω]은?
- 2
- 4
- 6
- 8
- 단자 a, b, c에 대칭 3상 전압을 인가하면, 각 선간 전압은 0V가 되어야 합니다. 이를 위해서는 a-b, b-c, c-a 각각의 전압차가 0V가 되어야 합니다. 따라서, a-b, b-c, c-a 각각의 저항이 같아야 하며, 이를 만족하는 저항값은 병렬 저항의 공식을 이용하여 구할 수 있습니다. R = (1/((1/2)+(1/2))) + (1/((1/2)+(1/2))) + (1/((1/2)+(1/2))) = 4 따라서, 정답은 "4"입니다.
19. 다음 R-L-C 직렬회로에서 스위치 S를 닫은 후에 흐르는 과도 전류의 파형 특성은?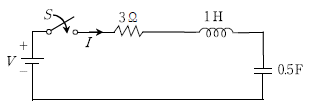
- 과제동(overdamped)
- 부족제동(underdamped)
- 임계제동(critically damped)
- 비제동(undamped)
- R-L-C 직렬회로에서 스위치 S를 닫으면, 전압이 갑자기 인가되어 전류가 급격하게 증가하게 됩니다. 이 때, R-L-C 회로는 2차 선형 상미분방정식을 따르게 되며, 이 방정식의 해는 3가지의 경우로 나뉩니다.
1. 과제동(overdamped) : R^2 > 4L/C 인 경우, 해는 2개의 서로 다른 실근을 가지며, 이 경우 과도한 감쇠가 일어나 전류가 천천히 증가합니다.
2. 부족제동(underdamped) : R^2 < 4L/C 인 경우, 해는 2개의 복소근을 가지며, 이 경우 과도한 진동이 발생하게 됩니다.
3. 임계제동(critically damped) : R^2 = 4L/C 인 경우, 해는 중근을 가지며, 이 경우 최대한 빠르게 감쇠하면서 진동이 없어집니다.
위의 회로에서 R-L-C 값이 주어지지 않았으므로, 해를 구할 수 없습니다. 하지만, 파형을 보면 전류가 천천히 증가하고 있으므로, 과제동(overdamped)인 것으로 추측할 수 있습니다. 따라서 정답은 "과제동(overdamped)"입니다.
20. 다음은 교류 정현파의 최댓값과 다른 값들과의 상관관계를 나타낸 것이다. 실효값 (A)와 파고율 (B)는? (순서대로 (A), (B))
- Vm/√2, 1/√2
- Vm/√2, √2
- √2Vm, 1/√2
- √2Vm, √2
- 정현파의 최댓값은 Vm이다.
실효값은 정현파의 최댓값인 Vm을 √2로 나눈 값이다. 이는 정현파의 최댓값이 아닌 경우에는 값이 작아지기 때문에, 최댓값과 다른 값들과의 상관관계를 비교할 때는 최댓값을 기준으로 비교하기 위해 √2로 나누어준다. 따라서 (A)의 정답은 Vm/√2이다.
파고율은 정현파의 최댓값과 유효값의 비율로, √2로 나눈 값이다. 이는 정현파의 최댓값이 아닌 경우에는 값이 작아지기 때문에, 최댓값과 다른 값들과의 상관관계를 비교할 때는 최댓값을 기준으로 비교하기 위해 √2로 나누어준다. 따라서 (B)의 정답은 √2이다.









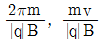
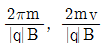
L = ΔΦ/Δi
여기서 ΔΦ는 시간에 따른 자기 플럭스 변화량이고, Δi는 시간에 따른 전류 변화량입니다.
주어진 문제에서는 전류가 0.1초 동안 20 A에서 4 A까지 일정한 비율로 변했다고 했으므로, Δi는 20 A - 4 A = 16 A입니다.
기전력은 다음과 같은 식으로 구할 수 있습니다.
ε = L(di/dt)
여기서 di/dt는 전류 변화율입니다. 주어진 문제에서는 전류가 0.1초 동안 변했으므로, di/dt = Δi/Δt = 16 A/0.1 s = 160 A/s입니다.
기전력이 20 V이므로, ε = 20 V입니다. 따라서,
20 V = L(160 A/s)
L = 20 V / 160 A/s = 0.125 H
따라서 정답은 "0.125"입니다.