1과목: 과목 구분 없음
1. 전압이 E [V], 내부저항이 r [Ω]인 전지의 단자 전압을 내부저항 25 [Ω]의 전압계로 측정하니 50 [V]이고, 75 [Ω]의 전압계로 측정하니 75 [V]이다. 전지의 전압 E [V]와 내부저항 r [Ω]은? (순서대로 E[V], r[Ω])
- 100, 25
- 100, 50
- 200, 25
- 200, 50
2. 등전위면(equipotential surface)의 특징에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄱ, ㄹ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
- ㄴ, ㄷ, ㄹ
3. 코일에 직류 전압 200 [V]를 인가했더니 평균전력 1,000 [W]가 소비되었고, 교류 전압 300 [V]를 인가했더니 평균전력 1,440 [W]가 소비되었다. 코일의 저항[Ω]과 리액턴스[Ω]는? (순서대로 저항[Ω], 리액턴스[Ω])
- 30, 30
- 30, 40
- 40, 30
- 40, 40
4. 다음 회로에서 스위치 S가 단자 a에서 충분히 오랫동안 머물러 있다가 t=0에서 단자 a에서 단자 b로 이동하였다. t > 0일 때의 전압 vc(t) [V]는?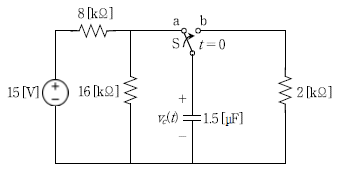
5. 독립전원과 종속전압원이 포함된 다음의 회로에서 저항 20 [Ω]의 전압 Va [V]는?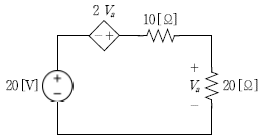
- -40
- -20
- 20
- 40
6. 다음 자기회로에 대한 설명으로 옳지 않은 것은? (단, 손실이 없는 이상적인 회로이다)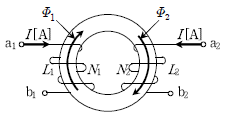
- b1과 a2를 연결한 합성 인덕턴스는 b1과 b2를 연결한 합성 인덕턴스보다 크다.
- 한 코일의 유도기전력은 상호 인덕턴스와 다른 코일의 전류 변화량에 비례한다.
- 권선비가 N1:N2=2 : 1일 때, 자기 인덕턴스 L1은 자기 인덕턴스 L2의 2배이다.
- 교류 전압을 변성할 수 있고, 변압기 등에 응용될 수 있다.
7. 전류 i(t)=t2+2t [A]가 1 [H] 인덕터에 흐르고 있다. t =1일 때, 인덕터의 순시전력[W]은?
- 12
- 16
- 20
- 24
8. 다음 회로에서 40 [μF] 커패시터 양단의 전압 Va [V]는?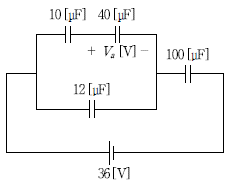
- 2
- 4
- 6
- 8
9. 그림과 같은 주기적인 전압 파형에 포함되지 않은 고조파의 주파수[Hz]는?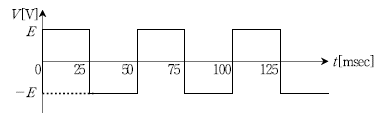
- 60
- 100
- 120
- 140
10. 다음 Y-Y 결선 평형 3상 회로에서 부하 한 상에 공급되는 평균전력[W]은? (단, 극좌표의 크기는 실횻값이다)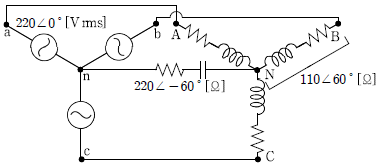
- 110
- 220
- 330
- 440
11. R-L-C 직렬회로에 100 [V]의 교류 전원을 인가할 경우, 이 회로에 가장 큰 전류가 흐를 때의 교류 전원 주파수 f [Hz]와 전류 I [A]는? (단, R =50 [Ω], L =100 [mH], C =1,000 [μF]이다) (순서대로 f[Hz],I[A])
- 50/π, 2
- 50/π, 4
- 100/π, 2
- 100/π, 4
12. 1대의 용량이 100 [kVA]인 단상 변압기 3대를 평형 3상 Δ결선으로 운전 중 변압기 1대에 장애가 발생하여 2대의 변압기를 V결선으로 이용할 때, 전체 출력용량[kVA]은?
- 100/√3
- 173/√3
- 220/√3
- 300/√3
13. 자속밀도 4[Wb/m2]의 평등자장 안에서 자속과 30° 기울어진 길이 0.5[m]의 도체에 전류 2[A]를 흘릴 때, 도체에 작용하는 힘 F[N]는?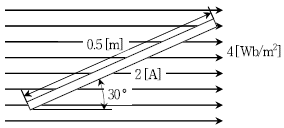
- 1
- 2
- 3
- 4
14. 다음 R-L 직렬회로에서 t=0에서 스위치 S를 닫았다. t=3에서 전류의 크기가 i(3)=4(1-e-1) [A]일 때, 전압 E [V]와 인덕턴스 L [H]은? (순서대로 E[V], L[H])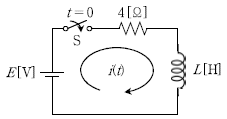
- 8, 6
- 8, 12
- 16, 6
- 16, 12
15. 다음 회로의 역률이 0.8일 때, 전압 Vs[V]와 임피던스 X [Ω]는? (단, 전체 부하는 유도성 부하이다) (순서대로 Vs[V], X[Ω])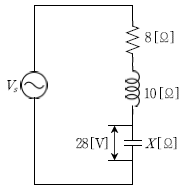
- 70, 2
- 70, 4
- 80, 2
- 80, 4
16. R-L 직렬회로에 직류 전압 100 [V]를 인가하면 정상상태 전류는 10 [A]이고, R-C 직렬회로에 직류 전압 100 [V]를 인가하면 초기전류는 10 [A]이다. 이 두 회로의 설명으로 옳지 않은 것은? (단, C=100 [μF], L=1 [mH]이고, 각 회로에 직류 전압을 인가하기 전 초깃값은 0이다)
- R-L 직렬회로의 시정수는 L이 10배 증가하면 10배 증가한다.
- R-L 직렬회로의 시정수가 R-C 직렬회로의 시정수보다 10배 크다.
- R-C 직렬회로의 시정수는 C가 10배 증가하면 10배 증가한다.
- R-L 직렬회로의 시정수는 0.1 [msec]다.
17. 다음 회로에서 전원 Vs [V]가 R-L-C로 구성된 부하에 인가 되었을 때, 전체 부하의 합성 임피던스 Z [Ω] 및 전압 Vs와 전류 I의 위상차 θ[°]는? (순서대로 Z[Ω], θ[°])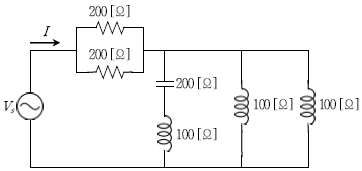
- 100, 45
- 100, 60
- 100√2, 45
- 100√2, 60
18. 다음 직류회로에서 4[Ω] 저항의 소비전력[W]은?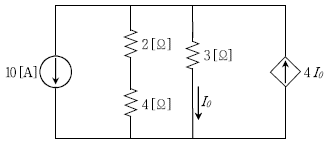
- 4
- 8
- 12
- 16
19. 다음 직∙병렬 회로에서 전류 I[A]의 위상이 전압 Vs[V]의 위상과 같을 때, 저항 R [Ω]은?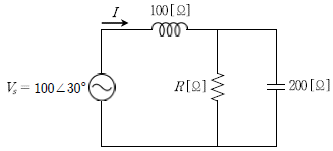
- 100
- 200
- 300
- 400
20. 그림과 같이 저항 R1=R2=10[Ω], 자기 인덕턴스 L1=10[H], L2=100 [H], 상호 인덕턴스 M=10 [H]로 구성된 회로의 임피던스 Zab[Ω]는? (단, 전원 Vs의 각속도는 ω=1[rad/s]이고 ZL=10-j100 [Ω]이다)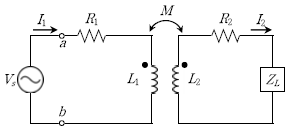
- 10-j15
- 10+j15
- 15-j10
- 15+j10






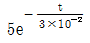
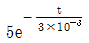
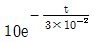
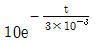
50 [V]의 경우, 전압계의 내부저항 25 [Ω]와 전지의 내부저항 r [Ω]가 직렬로 연결되어 전압을 측정하므로, 전압분배법칙에 따라 다음과 같은 식이 성립한다.
50 = E × (25 / (25 + r))
이를 정리하면,
E = 100 / (1 + r/25)
75 [V]의 경우도 같은 방법으로 계산하면,
75 = E × (75 / (75 + r))
이를 정리하면,
E = 300 / (4 + r/75)
두 식에서 E를 구하고, 이를 비교하여 r을 구할 수 있다. 구한 결과, "100, 25"가 정답이다.