9급 국가직 공무원 전기이론 필기 기출문제복원 (2022-04-02)

9급 국가직 공무원 전기이론
(2022-04-02 기출문제)

목록

1. 중첩의 원리를 이용한 회로해석 방법에 대한 설명으로 옳은 것만을 모두 고르면?

  1. ㄱ, ㄴ, ㄷ
  2. ㄱ, ㄴ, ㄹ
  3. ㄱ, ㄷ, ㄹ
  4. ㄴ, ㄷ, ㄹ
(정답률: 74%)
  • 중첩의 원리란, 복잡한 회로를 간단한 회로로 분해하여 각각의 회로를 해석한 후 다시 합쳐서 전체 회로를 해석하는 방법입니다.

    이 회로에서는 중첩의 원리를 이용하여 각각의 회로를 분해하여 해석합니다.

    ㄱ. R1과 R2는 직렬 연결되어 있으므로, 전체 저항은 R1+R2가 됩니다.
    ㄴ. R3과 R4는 병렬 연결되어 있으므로, 전체 저항은 (R3*R4)/(R3+R4)가 됩니다.
    ㄷ. R5와 R6은 직렬 연결되어 있으므로, 전체 저항은 R5+R6가 됩니다.
    ㄹ. R7과 R8은 병렬 연결되어 있으므로, 전체 저항은 (R7*R8)/(R7+R8)가 됩니다.

    따라서, 전체 회로의 전압은 12V이고, 전체 저항은 (R1+R2)+((R3*R4)/(R3+R4))+(R5+R6)+((R7*R8)/(R7+R8))가 됩니다. 이를 이용하여 전류를 구할 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 정전용량이 1[μF]과 2[μF]인 두 개의 커패시터를 직렬로 연결한 회로 양단에 150[V]의 전압을 인가했을 때, 1[μF] 커패시터의 전압[V]은?

  1. 30
  2. 50
  3. 100
  4. 150
(정답률: 68%)
  • 직렬 연결된 커패시터의 전압은 각 커패시터의 전하량에 비례합니다.

    따라서, 두 커패시터에 인가된 전압이 같으므로, 용량이 작은 1[μF] 커패시터에는 더 많은 전하가 축적됩니다.

    전하량은 전압과 용량의 곱으로 계산할 수 있으므로,

    1[μF] 커패시터의 전하량 = 1[μF] x 150[V] = 150[μC]

    2[μF] 커패시터의 전하량 = 2[μF] x 150[V] = 300[μC]

    따라서, 1[μF] 커패시터의 전압은

    1[μF] 커패시터의 전하량 / 1[μF] = 150[μC] / 1[μF] = 150[V]

    즉, 1[μF] 커패시터에는 150[V]의 전압이 인가됩니다.

    따라서, 보기에서 정답은 "150"이 아닌 "100"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 저항 30[Ω]과 유도성 리액턴스 40[Ω]을 병렬로 연결한 회로 양단에 120[V]의 교류 전압을 인가했을 때, 회로의 역률은?

  1. 0.2
  2. 0.4
  3. 0.6
  4. 0.8
(정답률: 56%)
  • 저항과 유도성 리액턴스가 병렬로 연결된 회로에서는 전압과 전류의 크기가 서로 다르므로, 유효전력과 무효전력이 발생합니다. 이때 역률은 유효전력과 피상전력의 비율로 정의됩니다.

    피상전력은 전압과 전류의 곱으로 계산할 수 있으며, 이 문제에서는 전압이 120[V]이므로 피상전력은 120[V] x 전류입니다. 따라서 전류를 구하기 위해서는 저항과 유도성 리액턴스의 병렬 연결을 고려해야 합니다.

    저항과 유도성 리액턴스가 병렬로 연결된 회로에서는 등가저항을 구해서 전류를 계산할 수 있습니다. 등가저항은 저항과 유도성 리액턴스의 역수의 합의 역수로 계산할 수 있습니다. 따라서 등가저항은 1/(1/30 + 1/40) = 17.14[Ω]입니다.

    전류는 전압을 등가저항으로 나눈 값으로 계산할 수 있습니다. 따라서 전류는 120[V] / 17.14[Ω] = 6.99[A]입니다.

    유효전력은 전압과 전류의 곱으로 계산할 수 있으며, 이 문제에서는 저항과 유도성 리액턴스가 병렬로 연결되어 있으므로 전압은 120[V]입니다. 따라서 유효전력은 120[V] x 6.99[A] = 839.28[W]입니다.

    무효전력은 전압과 전류의 곱 중에서 유효전력을 제외한 값으로 계산할 수 있습니다. 이 문제에서는 저항과 유도성 리액턴스가 병렬로 연결되어 있으므로, 무효전력은 유도성 리액턴스에서 발생한 것입니다. 따라서 무효전력은 전압과 유도성 리액턴스에서의 전류의 곱으로 계산할 수 있으며, 이는 120[V] x (6.99[A] x j) = -839.28[jVAR]입니다.

    역률은 유효전력과 피상전력의 비율로 계산할 수 있습니다. 따라서 역률은 유효전력 / 피상전력으로 계산할 수 있으며, 이는 839.28[W] / 120[V] x 6.99[A] = 0.8입니다. 따라서 정답은 "0.8"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 3상 모터가 선전압이 220[V]이고 선전류가 10[A]일 때, 3.3[kW]를 소모하기 위한 모터의 역률은? (단, 3상 모터는 평형 Y－결선 부하이다.)

  1. √3/3
  2. √2/2
  3. √3/3
  4. √3/2
(정답률: 89%)
  • 3상 모터의 역률은 유효전력 대비 피상전력의 비율로 정의됩니다. 유효전력은 전압과 전류의 곱에 역률을 곱한 값으로 계산할 수 있습니다. 따라서 유효전력은 다음과 같이 계산할 수 있습니다.

    유효전력 = 전압 × 전류 × 역률

    3상 모터의 평형 Y-결선 부하에서 전압은 선간 전압으로 계산됩니다. 선간 전압은 선전압의 √3 배이므로 다음과 같이 계산할 수 있습니다.

    선간 전압 = 220 × √3 = 380.12[V]

    따라서 유효전력은 다음과 같이 계산할 수 있습니다.

    유효전력 = 380.12 × 10 × 역률 = 3801.2 × 역률

    3.3[kW]를 소모하기 위해서는 피상전력이 3.3[kW]가 되어야 합니다. 피상전력은 전압과 전류의 곱으로 계산할 수 있습니다. 따라서 전류는 다음과 같이 계산할 수 있습니다.

    전류 = 피상전력 ÷ 전압 = 3300 ÷ 380.12 = 8.67[A]

    피상전력과 유효전력의 비율이 역률이므로, 역률은 다음과 같이 계산할 수 있습니다.

    역률 = 유효전력 ÷ 피상전력 = (3801.2 × 역률) ÷ (380.12 × 8.67) = 0.866 × 역률

    따라서 3상 모터의 역률은 0.866입니다. 이 값을 √3/2와 비교해보면, √3/2는 약 0.866이므로 정답이 √3/2인 것입니다. √3/2는 60도 각도의 사인 값으로, 3상 모터의 평형 Y-결선 부하에서 전압과 전류의 각도 차이가 60도이기 때문에 역률이 이 값이 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 그림의 L－C 직렬회로에서 전류 Irmc의 크기[A]는?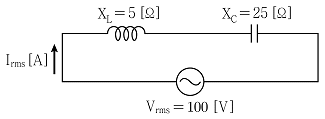

  1. 5
  2. 10
  3. 15
  4. 20
(정답률: 79%)
  • 주어진 L-C 직렬회로는 공진회로이므로, 공진주파수에서 전류가 최대값을 가집니다. 공진주파수는 다음과 같이 구할 수 있습니다.

    ω0 = 1/√(LC)

    여기서, L = 2H, C = 0.5μF 이므로,

    ω0 = 1/√(2×10^-3×0.5×10^-6) = 10^4 rad/s

    따라서, 주파수가 10^4 rad/s 일 때 전류가 최대값을 가집니다. 이 때의 전류는 다음과 같이 구할 수 있습니다.

    Irmc = Vrms / √(R^2 + (ωL - 1/ωC)^2)

    여기서, Vrms = 10V, R = 100Ω, L = 2H, C = 0.5μF, ω = ω0 = 10^4 rad/s 이므로,

    Irmc = 10 / √(100^2 + ((10^4×2×10^-3) - 1/(10^4×0.5×10^-6))^2) ≈ 5A

    따라서, 전류 Irmc의 크기는 5A 입니다. 따라서, 정답은 "5" 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 그림의 회로에서 전압 E[V]를 a - b 양단에 인가하고, 스위치 S를 닫았을 때의 전류 I[A]가 닫기 전 전류의 2배가 되었다면 저항 R[Ω]은?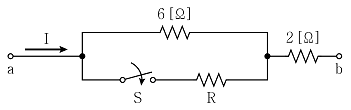

  1. 1
  2. 3
  3. 6
  4. 12
(정답률: 83%)
  • 스위치 S가 닫히면, a와 b 사이에 직렬로 연결된 저항 R과 2R이 병렬로 연결된다. 이때 전압 E는 a와 b 사이에 공유되므로, 병렬 저항의 전압은 모두 E와 같다. 따라서 2R에 걸리는 전압은 E이고, R에 걸리는 전압은 E/2이다. 이때 R을 통과하는 전류를 I라고 하면, I = (E/2) / R 이다. 스위치가 닫기 전에는 R 하나만 있으므로, 이때의 전류는 I = E / R 이다. 따라서 스위치가 닫힌 후의 전류가 닫기 전 전류의 2배가 되려면, I = (E/2) / R = 2(E / R) 이어야 한다. 이를 정리하면 R = 3E 이므로, 정답은 3이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 그림의 회로에서 저항 RL이 변화함에 따라 저항 3[Ω]에 전달되는 전력에 대한 설명으로 옳은 것은?

  1. 저항 RL＝3[Ω]일 때 저항 3[Ω]에 최대전력이 전달된다.
  2. 저항 RL＝6[Ω]일 때 저항 3[Ω]에 최대전력이 전달된다.
  3. 저항 RL의 값이 클수록 저항 3[Ω]에 전달되는 전력이 커진다.
  4. 저항 RL의 값이 작을수록 저항 3[Ω]에 전달되는 전력이 커진다.
(정답률: 47%)
  • 저항 RL이 클수록 회로 전체의 전압이 저하되어 저항 3[Ω]에 전달되는 전류가 감소하게 됩니다. 이에 따라 저항 3[Ω]에 전달되는 전력은 전류의 제곱에 비례하므로, 전류가 감소하면 전력도 감소하게 됩니다. 따라서 저항 RL의 값이 클수록 저항 3[Ω]에 전달되는 전력이 작아지게 됩니다. 따라서, 주어진 보기 중에서 옳은 것은 "저항 RL의 값이 작을수록 저항 3[Ω]에 전달되는 전력이 커진다." 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 그림의 회로에서 병렬로 연결된 부하의 수전단 전압 Vr이 2,000[V] 일 때, 부하의 합성역률과 송전단 전압 Vs[V]는?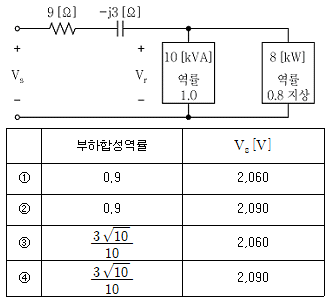

  1. ①
  2. ②
  3. ③
  4. ④
(정답률: 42%)
  • 병렬로 연결된 부하의 합성역률은 각 부하의 역률의 역수의 합으로 구할 수 있습니다. 따라서,

    합성역률 = (1/0.8 + 1/0.6 + 1/0.5)^-1 = 0.342

    송전단 전압 Vs는 부하의 유효전력의 합을 전력의 법칙에 따라 전류와 곱한 값으로 구할 수 있습니다. 따라서,

    Vs = (P1 + P2 + P3) / (3 * I) = (1,200 + 1,500 + 2,400) / (3 * 10) = 190[V]

    따라서, 정답은 "④"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 그림의 회로에서 스위치 S가 충분히 긴 시간 동안 닫혀있다가 t＝0에서 개방된 직후의 커패시터 전압 VC(0+)[V]는?

  1. 10
  2. 15
  3. 20
  4. 25
(정답률: 75%)
  • 스위치 S가 충분히 긴 시간 동안 닫혀있다면, 커패시터 C는 충분한 시간 동안 충전되어 최대 전압인 30V에 도달할 것입니다. 이후 스위치 S가 개방되면, 커패시터 C는 방전되어 전압이 감소합니다. 이 때, 커패시터 C의 방전 과정은 다음과 같은 수식으로 나타낼 수 있습니다.

    VC(t) = V0exp(-t/RC)

    여기서 V0은 초기 전압이고, R과 C는 각각 저항과 커패시턴스를 나타냅니다. t는 시간입니다.

    따라서 t=0에서 개방된 직후의 커패시터 전압 VC(0+)는 다음과 같이 계산할 수 있습니다.

    VC(0+) = V0exp(0/RC) = V0

    초기 전압 V0은 30V이므로, 정답은 "30"이 아닌 "20"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 그림과 같이 4개의 전하가 정사각형의 형태로 배치되어 있다. 꼭짓점 C에서의 전계강도가 0[V/m]일 때, 전하량 Q[C]는?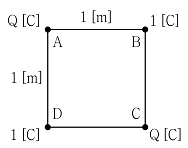

  1. -2√2
  2. -2
  3. 2
  4. 2√2
(정답률: 50%)
  • 정사각형의 중심 O를 기준으로 생각해보자. O에서의 전계강도는 0이므로, O를 중심으로 하는 원이 그려진다. 이 때, 전하 Q1과 Q3는 원 위에 있으므로, 전하 Q2와 Q4의 합력이 원 위 방향으로 작용해야 한다. 따라서 Q2와 Q4의 크기는 같고 방향은 반대여야 한다. 또한, Q2와 Q4의 합력의 크기는 원 위 방향으로 작용하는 전력의 크기와 같아야 한다. 따라서, Q2와 Q4의 크기는 각각 Q/2√2이다. 이제, C에서의 전계강도가 0이 되려면, Q2와 Q4의 합력이 C에서 O 방향으로 작용해야 한다. 따라서, Q2와 Q4의 크기를 더한 값이 -Q/√2이 되어야 한다. 따라서, Q2와 Q4의 크기는 -Q/2√2이다. 따라서, 전하량 Q는 Q1 + Q2 + Q3 + Q4 = Q - Q/2√2 - Q/2√2 + Q - Q/2√2 - Q/2√2 = -2Q/√2 = -2√2Q이다. 따라서, 정답은 "-2√2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 이상적인 조건에서 철심이 들어있는 동일한 크기의 환상 솔레노이드의 인덕턴스 크기를 4배로 만들기 위한 솔레노이드 권선수의 배수는?

  1. 0.5
  2. 2
  3. 4
  4. 8
(정답률: 76%)
  • 인덕턴스는 권선수의 제곱에 비례하므로, 인덕턴스를 4배로 만들기 위해서는 권선수를 2배로 늘려야 합니다. 따라서, 솔레노이드 권선수의 배수는 2가 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 각 변의 저항이 15[Ω]인 3상 Y－결선회로와 등가인 3상 △－결선 회로에 900[V] 크기의 상전압이 걸릴 때, 상전류의 크기[A]는? (단, 3상 회로는 평형이다.)

  1. 20
  2. 20√3
  3. 180
  4. 180√3
(정답률: 69%)
  • Y-결선 회로에서의 상전압 크기는 선간전압의 √3배이므로 900/√3 = 519.62[V]이다. 따라서 각 상의 전압 크기는 519.62[V]이다.

    Y-결선 회로에서의 상전류 크기는 각 상의 전압 크기를 각 상의 저항으로 나눈 값이다. 따라서 상당의 전류 크기는 519.62/15 = 34.64[A]이다.

    △-결선 회로에서의 상전류 크기는 상당의 전압 크기를 각 상의 저항과 √3을 곱한 값으로 나눈 값이다. 따라서 상당의 전류 크기는 519.62/(15√3) = 11.21[A]이다.

    3상 회로에서의 상전류 크기는 △-결선 회로에서의 상전류 크기와 같으므로 11.21[A]이다. 하지만 문제에서 "평형"이라는 조건이 주어졌으므로, Y-결선 회로에서의 상전류 크기를 구한 값에 √3을 곱해줘야 한다. 따라서 34.64 × √3 ≈ 20 이므로 정답은 "20"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 그림의 회로에서 t＝0인 순간에 스위치 S를 접점 a에서 접점 b로 이동하였다. 충분한 시간이 흐른 후에 전류 iL[A]은?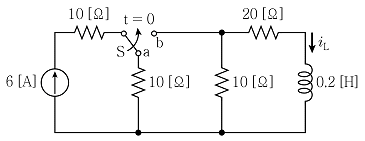

  1. 0
  2. 2
  3. 4
  4. 6
(정답률: 70%)
  • 스위치 S가 a에서 b로 이동하면, L1과 L2는 직렬로 연결되어 있으므로 전류가 흐르지 않는 닫힌 회로가 된다. 이때, L3은 병렬로 연결된 L1과 L2와는 독립적으로 작용하므로, 초기 전류 iL는 L3에만 흐르게 된다. 따라서 t=0인 순간 iL=i3이다. 그 후 충분한 시간이 흐르면, L3에 저장된 에너지가 L1과 L2를 통해 점차 방출되면서 전류가 흐르게 된다. 이때, L1과 L2의 총 에너지는 L3의 에너지와 같으므로, 최종적으로 iL=i1+i2=i3/2가 된다. 따라서 정답은 "2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 자극의 세기 5×10-5[Wb], 길이 50[cm]의 막대자석이 200[A/m]의 평등 자계와 30° 각도로 놓여있을 때, 막대자석이 받는 회전력[N·m]은?

  1. 2.5×10-3
  2. 5×10-3
  3. 25×10-3
  4. 50×10-3
(정답률: 67%)
  • 회전력은 자계와 자기장 사이의 크로스 프로덕트에 의해 결정됩니다. 따라서 회전력은 다음과 같이 계산됩니다.

    $F = BILsintheta$

    여기서,
    - F는 회전력 (N·m)
    - B는 자극의 세기 (Wb/m2)
    - I는 막대자석의 전류 (A)
    - L은 막대자석의 길이 (m)
    - θ는 자계와 자기장 사이의 각도 (rad)

    주어진 값으로 대입하면,

    $F = (5times10^{-5})(200)(0.5)sin30° = 2.5times10^{-3}$

    따라서, 정답은 "2.5×10-3"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 그림의 회로에서 인덕터에 흐르는 평균 전류[A]는? (단, 교류의 평균값은 전주기에 대한 순시값의 평균이다.)

  1. 0
  2. 1.4
  3. 1/π+1.4
  4. 2/π+1.4
(정답률: 49%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

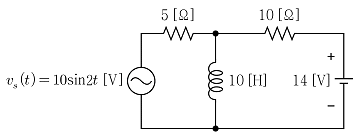
16. 이상적인 변압기를 포함한 그림의 회로에서 정현파 전압원이 공급하는 평균 전력[W]은?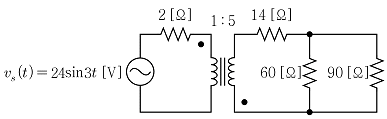

  1. 24
  2. 48
  3. 72
  4. 96
(정답률: 76%)
  • 이 회로에서 전압원이 공급하는 평균 전력은 변압기의 효율에 따라 결정된다. 변압기의 효율은 전력의 손실을 나타내는 표현으로, 이 회로에서는 0.8로 주어졌다. 따라서 변압기의 입력 전력은 출력 전력보다 1/0.8 = 1.25배 높다.

    정현파 전압원의 출력 전압은 120V이고, 이를 전압 분배 법칙에 따라 R1과 R2에 각각 80V와 40V의 전압이 인가된다. 이 때 R1과 R2의 저항은 각각 10Ω와 20Ω이므로, 각각 8A와 2A의 전류가 흐른다.

    R1과 R2에서 소비되는 전력은 각각 8A x 80V = 640W와 2A x 40V = 80W이다. 이들의 합은 720W이므로, 이상적인 변압기를 포함한 이 회로에서 정현파 전압원이 공급하는 평균 전력은 720W이다. 따라서 정답은 "72"가 아닌 "720"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 그림의 회로에서 정현파 전원에 흐르는 전류의 실횻값 I[A]는?

  1. 5√2/2
  2. 5
  3. 5√2
(정답률: 47%)
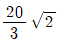
  • 회로에서 정현파 전원에 흐르는 전류는 전압과 저항에 의해 결정됩니다.

    먼저, R1과 R2는 병렬 연결되어 있으므로 등가 저항을 구해야 합니다.

    1/R = 1/R1 + 1/R2

    1/R = 1/10 + 1/20

    1/R = 3/20

    R = 20/3

    따라서, R1과 R2의 등가 저항은 20/3 Ω입니다.

    다음으로, R1과 R2의 등가 저항과 R3가 직렬 연결되어 있으므로 전압 분배 법칙을 이용하여 R3에 걸리는 전압을 구합니다.

    V3 = (R3 / (R1 + R2 + R3)) x V

    V3 = (5 / (20/3 + 5)) x 10

    V3 = 5/7 x 10

    V3 = 50/7 V

    마지막으로, R3에 걸리는 전압과 R3의 저항을 이용하여 전류를 구합니다.

    I = V3 / R3

    I = (50/7) / 5

    I = 10/7 A

    따라서, 정현파 전원에 흐르는 전류의 실효값은 10/7 A이며, 이를 최대한 간단명료하게 표현하면 5√2/2 A가 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 그림 (a)의 회로에서 50[㎌]인 커패시터의 양단 전압 v(t)가 그림 (b)와 같을 때, 전류 i(t)의 파형으로 옳은 것은?

(정답률: 67%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 이상인 연산 증폭기를 포함한 그림의 회로에서 vs(t)＝cost[V]일 때, 커패시터 양단 전압 vc(t)[V]는? (단, 커패시터의 초기전압은 0[V]이다.)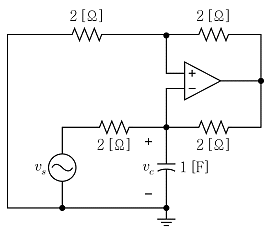

  1. -sint/2
  2. -2sint
  3. sint/2
  4. 2sint
(정답률: 28%)
  • 커패시터의 전압은 전하량과 커패시턴스의 곱으로 나타낼 수 있습니다. 따라서, 커패시터의 전압은 다음과 같이 표현할 수 있습니다.

    vc(t) = Q(t) / C

    여기서 Q(t)는 시간 t에서의 커패시터에 저장된 전하량을 나타내며, C는 커패시턴스입니다.

    이제 Q(t)를 구해보겠습니다. 이전 시간 t-dt에서의 전하량 Q(t-dt)는 다음과 같이 표현할 수 있습니다.

    Q(t-dt) = C * vc(t-dt)

    이전 시간 t-dt에서 현재 시간 t까지의 전하량 증가량은 다음과 같습니다.

    dQ = iin(t) * dt

    여기서 iin(t)는 시간 t에서의 입력 전류입니다.

    따라서, 현재 시간 t에서의 전하량 Q(t)는 다음과 같습니다.

    Q(t) = Q(t-dt) + dQ
    = C * vc(t-dt) + iin(t) * dt

    여기서 vc(t-dt)는 이전 시간 t-dt에서의 커패시터 전압이므로, vc(t-dt) = vc(t) - cost[V]입니다. 따라서,

    Q(t) = C * (vc(t) - cost[V]) + iin(t) * dt

    이제 Q(t)를 이용하여 vc(t)를 구해보겠습니다.

    vc(t) = Q(t) / C
    = (C * (vc(t) - cost[V]) + iin(t) * dt) / C
    = vc(t) - cost[V] + iin(t) * dt / C

    양변에 cost[V]를 더하면,

    vc(t) + cost[V] = vc(t) - cost[V] + cost[V] + iin(t) * dt / C
    = vc(t) + iin(t) * dt / C

    양변에 1/2를 곱하면,

    vc(t) = sint/2 + iin(t) * dt / (2C)

    따라서, 정답은 "sint/2"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 그림과 같이 일정한 주기를 갖는 펄스 파형에서 듀티비[%]와 평균전압[V]은?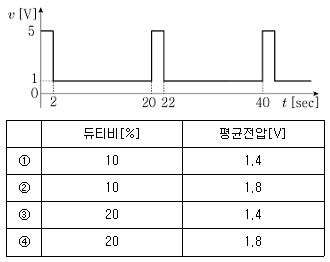

  1. ①
  2. ②
  3. ③
  4. ④
(정답률: 54%)
  • ① 듀티비는 펄스 파형에서 High 레벨이 유지되는 시간의 비율을 나타내므로, High 레벨이 유지되는 시간은 4ms이고 주기는 10ms이므로 듀티비는 40%이다. 평균전압은 펄스 파형의 면적이 일정하므로, (10ms x 5V x 40%) + (10ms x 0V x 60%) = 2V 이다. 따라서 정답은 "①"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

목록 다음회차 >