1과목: 과목 구분 없음
1. 철근콘크리트가 성립할 수 있는 이유로 옳지 않은 것은?
- 철근과 콘크리트 사이의 부착강도가 커서 일체식 구조형성이 가능하다.
- 철근을 감싸는 콘크리트가 철근의 부식을 막아준다.
- 철근과 콘크리트의 탄성계수가 비슷하여 변형률이 비슷하다.
- 철근과 콘크리트의 열팽창계수가 거의 동일하여 온도에 대한 신축이 거의 같다.
2. 철근의 설계기준 항복강도와 지배단면 변형률 한계 사이의 관계가 옳지 않은 것은 ?
- 철근의 항복강도가 300MPa일 때, 압축지배 변형률 한계는 0.0015이고, 인장지배 변형률 한계는 0.005이다.
- 철근의 항복강도가 350MPa일 때, 압축지배 변형률 한계는 0.00175이고, 인장지배 변형률 한계는 0.005이다.
- 철근의 항복강도가 400MPa일 때, 압축지배 변형률 한계는 0.002이고, 인장지배 변형률 한계는 0.005이다.
- 철근의 항복강도가 500MPa일 때, 압축지배 변형률 한계는 0.0025이고, 인장지배 변형률 한계는 0.005이다.
3. 프리스트레스트 콘크리트(PSC)의 설계 시 균열검토를 수행해야 하는 이유로 옳지 않은 것은?
- 균열로 인해 PS 강재의 인장응력이 감소되어 보의 피로 저항성이 감소되기 때문
- 균열을 수반할 때 발생되는 휨강성의 감소에 따라서 처짐이 영향을 받기 때문
- 보에 균열이 발생하면 PS 강재는 부식에 취약해지기 때문
- 균열은 수밀성을 요하는 구조물에서 누수의 원인이 되기 때문
4. 보통의 골재를 사용한 콘크리트의 설계기준강도 fck=19MPa 일 때 콘크리트의 탄성계수[MPa]는?
- 20,487
- 22,681
- 25,500
- 37,051
5. 기둥에서 장주와 단주의 구별에 대한 설명으로 옳지 않은 것은?
- 횡구속 골조구조에서
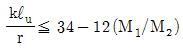 조건을 만족하는 경우에는 단주로 간주할 수 있다.
조건을 만족하는 경우에는 단주로 간주할 수 있다. - ①번 항목에서 [34-12(M1/M2)] 값은 40을 초과할 수 없다.
- M1/M2의 값은 기둥이 단일 곡률일 때 양(+)으로 이중곡률일 때 음(-)으로 취하여야 한다.
- 비횡구속 골조구조의 경우
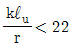 조건을 만족하는 경우에는 장주로 간주할 수 있다.
조건을 만족하는 경우에는 장주로 간주할 수 있다.
6. 길이가10m인캔틸레버보에자중을포함한계수하중 ωu=20kN/m가 작용할 때 전단철근이 필요한 구간 x[m]는? (단, 최소전단철근 배근 구간은 제외한다. 그리고 폭 b=400mm, 유효깊이 d=600mm, fck=25MPa 이다)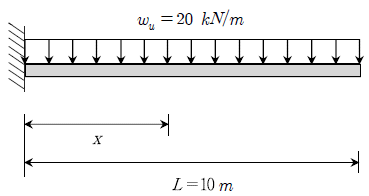
- 2.5
- 3.0
- 3.5
- 4.0
7. PS 강재의 탄성계수 Eps=2×105MPa이고 콘크리트의 건조 수축률 ϵsh=25×10-5일 때, 콘크리트 건조수축에 의한 PS 강재의 프리스트레스 감소율을 5%로 제어하기 위한 초기 프리 스트레스 값[MPa]은?
- 1,000
- 2,000
- 3,000
- 4,000
8. 그림과 같이 콘크리트 기초판과 기둥의 중심에 수직하중과 모멘트가 작용하고 있다. 콘크리트 기초판과 기초 지반 사이에 인장응력이 작용하지 않도록 하기 위한 최소 수직하중[kN]은? (단, 자중에 의한 하중효과는 무시하고, 하중계수는 고려하지 않는다)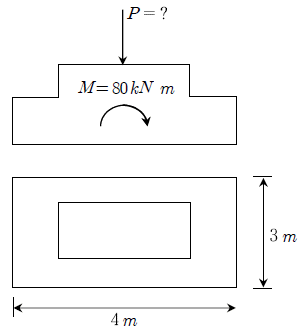
- 110
- 120
- 130
- 140
9. 지속하중에 의한 탄성처짐이 20mm 발생한 캔틸레버보의 5년간의 장기처짐을 포함한 총처짐[mm]은? (단, 보의 인장철근비는 0.06, 압축철근비는 0.02, 지속하중의 재하기간에 따른 계수는 2.0 이다)
- 20
- 30
- 40
- 50
10. 철근콘크리트 구조물의 전단과 비틀림 설계에 대한 설명으로 옳지 않은 것은?
- 받침부로부터 d이내에 위치한 단면은 d에서 구한 계수전단력 Vu의 값으로 설계할 수 있다.
- 철근콘크리트 부재에서 계수 비틀림 모멘트 Tu가
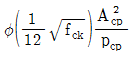 보다 작으면 비틀림의 영향을 무시할 수 있다.
보다 작으면 비틀림의 영향을 무시할 수 있다. - 비틀림에 저항하기 위해서는 폐쇄스터럽만 필요하고 종방향 철근은 고려하지 않는다.
- 비틀림 설계 시에 폐쇄스터럽은 비틀림과 전단에 대한 스터럽 필요량을 함께 고려한다.
11. 휨과 압축을 받는 직사각형 단주의 설계에 대한 설명으로 옳지 않는 것은?
- 균형상태는 압축측 연단의 콘크리트 변형률이 0.003에 도달함과 동시에 철근의 응력이 항복강도 fy에 도달되는 상태를 말한다.
- 균형상태에서 중립축위치
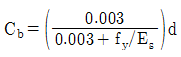 이고, 압축부 콘크리트의 등가응력사각형깊이 ab=β1Cb이다.
이고, 압축부 콘크리트의 등가응력사각형깊이 ab=β1Cb이다. - 압축지배인 경우에 띠철근 기둥의 강도감소계수는 0.70이고, 나선철근기둥의 강도감소계수는 0.75이다.
- 기둥강도상관도(P-M 상관도)에서 편심(e)<균형편심(eb) 이면 기둥강도는 콘크리트의 압축으로 지배된다.
12. 프리스트레스트 콘크리트 부재에 프리스트레스 도입으로 인한 콘크리트 압축응력 fcs=5MPa이고, 콘크리트 크리프계수 Cu=2.0, 탄성계수비 n=6일 때, 콘크리트 크리프에 의한 PS 강재의 프리스트레스 감소량[MPa]은?
- 40
- 50
- 60
- 70
13. 표준갈고리에 대한 설명으로 옳지 않은 것은?
- 주철근의 경우 180° 표준 갈고리는 구부린 반원 끝에서 4db이상, 또한 40mm이상 더 연장해야 한다.
- 주철근의 경우 90° 표준 갈고리는 구부린 끝에서 12db 이상 더 연장해야 한다.
- 스터럽 또는 띠철근의 경우 135° 표준 갈고리에서 D25 이하의 철근은 구부린 끝에서 6db이상 더 연장해야 한다.
- 스터럽 또는 띠철근의 경우 90° 표준 갈고리에서 D16 이하의 철근은 구부린 끝에서 6db이상 더 연장해야 한다.
14. 플레이트 거더의 보강재에 대한 설명으로 옳지 않은 것은 ?
- 수직보강재의 폭은 복부판 높이의 1/30에 50mm를 가산한 것보다 크게 잡는 것이 좋다.
- 수직보강재의 간격은 지점부에서 복부판 높이의 2.0배 이하, 그 밖에는 2.5배 이하까지 허용되지만, 일반적으로 복부판 높이 보다 작게 선택한다.
- 수평보강재와 수직보강재는 복부판의 같은 쪽에 붙일 필요는 없지만 같은 쪽에 붙일 경우 수평보강재는 수직보강재 사이 에서 되도록 폭을 넓혀 붙인다.
- 수평보강재를 1단 설치하는 경우 압축플랜지에서 0.2h(h는 복부판 높이)부근, 2단 설치하는 경우에는 0.14h와 0.36h부근에 설치하는 것을 원칙으로 한다.
15. 옹벽의 안정검토에 대한 설명으로 옳지 않은 것은? (단, ∑H는 수평력의 합, y는 기초저판 아래면에서 수평력 작용점까지의 높이, ∑V는 수직력의 합, x는 기초저판 앞면에서 수직력 작용점까지의 거리, μ는 마찰계수, B는 기초저판의 폭이다)
- 전도모멘트 Mo=(∑H)y이고, 저항모멘트 Mr=(∑V)x이면, 전도안전율=Mr/Mo≧2.0이다.
- 저판의밑면과지반사이에발휘될수있는마찰저항력 Hr=μ(∑V)이고, Ho=∑H이면, 활동안전율=Hr/Ho≧1.5이다.
- 지반의 허용지지력을 극한지지력 qu로부터 구하는 경우, 지반의 허용지지력 qa=qu/3을 취한다.
- 편심거리 e≦B/6이면, 최대지반반력
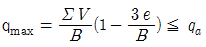 이다.
이다.
16. 도로교 내진설계 시 고려사항으로 옳지 않은 것은 ?
- 거더의 단부에서는 최소 받침지지길이가 확보되어야 한다.
- 상부구조의 여유간격은 지진 시의 지반에 대한 상부구조의 총변위량 만으로 산정한다.
- 최소 받침지지길이의 확보가 어려울 경우에 낙교방지를 위해 변위구속장치를 설치해야 한다.
- 지진시 상부구조와 교대 혹은 인접하는 상부구조간의 충돌에 의한 주요 구조부재의 손상을 방지해야 한다.
17. 그림과 같이 지간이 8m인 프리스트레스트 콘크리트 단순보에 PS 강재가 직선으로 단면의 도심에 배치되어 있고 1,200kN의 프리스트레스 힘이 작용하고 있다. 보의 단위중량을 25kN/m3로 가정할 때, 보의 중앙단면 하연의 응력이 0(zero) 이 되도록 하기 위해 자중 외에 추가로 가해 주어야 하는 등분포하중 ω[kN/m]은?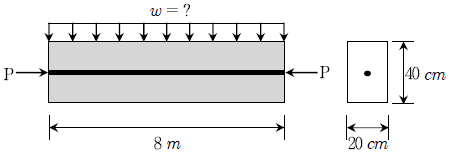
- 8
- 10
- 12
- 14
18. 그림과 같은 연결에서 볼트가 지지할 수 있는 인장력[kN]은? (단, 허용전단응력 vsa=200MPa, 허용지압응력 fba=300MPa, π=3으로 계산한다)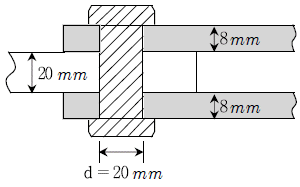
- 64
- 96
- 120
- 180
19. 그림과 같은 철근콘크리트 T형보의 휨강도 계산시 플랜지 상연에서 중립축까지의 거리와 가장 가까운 값[mm]은? (단, 콘크리트 압축강도 fck=25MPa, 철근의 항복강도 fy=300MPa, 철근 단면적 As=5,000mm2이다)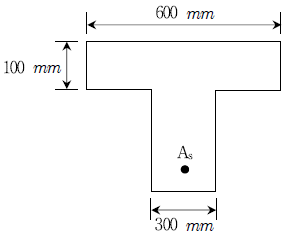
- 130
- 140
- 150
- 160
20. 압축과 휨을 받는 띠철근 기둥(단주)이 그림과 같은 변형률 분포를 나타낼 때 도심으로부터 편심을 갖는 공칭 축하중강도 Pn[kN]는? (단, 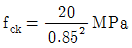 , Es=2.0×105MPa이다. 또한 압축철근은 항복한 것으로 가정하고, 철근의 압축력 Cs=As′fy를 사용한다)
, Es=2.0×105MPa이다. 또한 압축철근은 항복한 것으로 가정하고, 철근의 압축력 Cs=As′fy를 사용한다)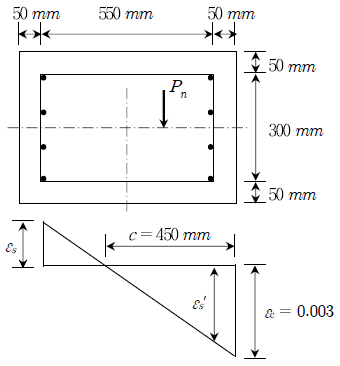
- 3,125
- 3,625
- 3,850
- 4,125





