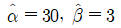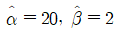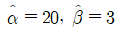1과목: 과목 구분 없음
1. 다음 상자그림에 대한 설명으로 옳은 것은?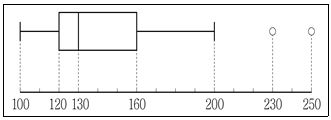
- 자료의 표준편차는 150이다.
- 자료의 중앙값은 130이다.
- 자료의 최빈값이 중앙값보다 크다.
- 자료의 사분위수범위는 100이다.
2. n개의 자료 (xi, yi) (i = 1, 2, …, n)의 표본상관계수는 0.2이다. vi = xi + 1, wi = 2yi - 1 이라고 할 때, 변환된 n개의 자료 (vi, wi) (i = 1, 2, …, n)의 표본상관계수는?
- 0.2
- 0.3
- 0.4
- 0.5
3. 어느 회사에서 차량 내비게이션을 연령대가 30대부터 50대까지인 고객에게 한 달 동안 사용하게 한 후 구매 의사를 알아보기 위해 240명을 임의추출하여 다음과 같은 분할표를 작성하였다. 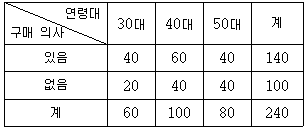
연령대와 구매 의사는 서로 독립이라는 귀무가설을 검정하기 위한 카이제곱통계량의 p-값(유의확률)이 0.128 일 때, 이에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄴ
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄱ, ㄴ, ㄷ
4. 단순선형회귀모형 yi = α+βxi+εi (i = 1, 2, …, n)에서 최소제곱법에 의하여 추정된 회귀계수를 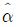 와
와 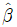 , yi의 예측값을
, yi의 예측값을 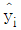 , 잔차를
, 잔차를 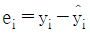 , 총제곱합(SST)을
, 총제곱합(SST)을 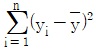 , 회귀제곱합(SSR)을
, 회귀제곱합(SSR)을 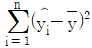 , 잔차제곱합(SSE)을
, 잔차제곱합(SSE)을 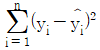 이라고 할 때, 이에 대한 설명으로 옳지 않은 것은? (단, εi는 N(0, σ2)을 따르고 서로 독립이다)
이라고 할 때, 이에 대한 설명으로 옳지 않은 것은? (단, εi는 N(0, σ2)을 따르고 서로 독립이다)
- SSE는 σ2의 불편추정량(unbiased estimator)이다.
- 결정계수(R2)는 SSR/SST 이다.
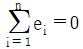 이다.
이다.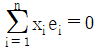 이다.
이다.
5. 어느 대학교의 4개 단과대학인 인문대, 사회대, 자연대, 공대에서 각각 50명씩 임의추출하여 남학생과 여학생의 수를 조사한 분할표가 다음과 같다. 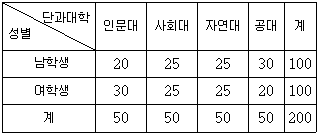
4개 단과대학의 남학생 비율이 모두 같다는 귀무가설을 검정하기 위한 카이제곱통계량의 값과 유의수준 5%에서 검정 결과를 옳게 짝지은 것은? (단, χ2α(k)는 자유도가 k인 카이제곱분포의 제100×(1-α) 백분위수를 나타낼 때 χ20.05(3)=7.81, χ20.05(4)=9.49 이다)
- ①
- ②
- ③
- ④
6. 확률변수 X에 대하여 E[X(X-1)]=3, E[X(X+1)]=5 일 때, X의 분산은?
- 3
- 4
- 5
- 6
7. 갑, 을 두 사람이 가위바위보 게임을 10회 시행하여 갑이 이기는 횟수를 확률변수 X라 할 때, 이에 대한 설명으로 옳은 것은? (단, 갑, 을은 각자 임의로 가위, 바위, 보 중에서 하나를 내고, 비기는 경우도 1회 시행으로 간주한다)
- X의 확률분포는 대칭이다.
- 확률변수 Y = 10-X는 10회의 시행에서 갑이 지는 횟수이다.
- Var(X) = 5/2 이다.
- E(3X+5) = 15 이다.
8. 단순선형회귀모형 yi = α+βxi+εi (i = 1, 2, …, )에 최소제곱법을 적용하여 얻은 분산분석표의 일부가 다음과 같을 때, 이에 대한 설명으로 옳지 않은 것은? (단, εi는 N(0, σ2)을 따르고 서로 독립이다)
- ㉠과 ㉡의 값은 각각 1과 2이다.
- F-값은 회귀평균제곱(MSR)을 잔차평균제곱(MSE)으로 나눈 값이다.
- 전체 자료의 수 n은 19이다.
- 유의수준 5%에서 회귀모형이 유의하다.
9. 정규분포 N(μ, σ2)을 따르는 모집단에서 n개의 표본을 임의추출하여 구한 μ의 95% 신뢰구간이 (-0.1, 0.7)일 때, 이에 대한 설명으로 옳지 않은 것은?
- 가설 H0 : μ = 0 대 H1 : μ ≠ 0 을 검정할 때 유의수준 5%에서 귀무가설을 기각하지 못한다.
- 표본평균은 0.3이다.
- μ가 구간 (-0.1, 0.7)에 속하지 않을 확률은 0.05 이다.
- μ의 90% 신뢰구간의 길이는 0.8보다 작다.
10. 어느 회사 신입사원의 입사 시험성적은 평균이 μ인 정규분포를 따른다고 한다. 신입사원 중에서 n명을 임의추출하여 구한 시험성적의 표본평균은 60보다 크고, 가설 H0 : μ = 60대 H1 : μ ≠ 60에 대한 p-값은 0.1이었다. 동일한 표본에 대해 가설 H0 : μ = 60 대 H1 : μ > 60에 대한 p-값은 a이고, 가설 H0 : μ = 60 대 H1 : μ < 60에 대한 p-값은 b일 때, b-a의 값은?
- 0.05
- 0.1
- 0.9
- 0.95
11. 50개의 관측값을 가장 작은 값부터 가장 큰 값까지 크기순으로 나열하여 x(1), x(2), …, x(50)으로 나타낼 때, 이에 대한 설명으로 옳지 않은 것은?
- 제20 백분위수는 x(20)이다.
- 제3 사분위수는 x(38)이다.
- 중앙값은
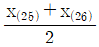 이다.
이다. - 사분위수범위는
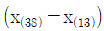 이다.
이다.
12. 10개의 자료 (x1, y1), (x2, y2), …, (x10, y10)에 대하여 단순선형회귀모형 yi = α+βxi+εi (i = 1, 2, …, 10)를 적합하고자 한다. 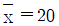 ,
, 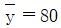 ,
, 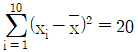 ,
, 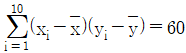 일 때, 최소제곱법을 이용하여 추정한 회귀계수
일 때, 최소제곱법을 이용하여 추정한 회귀계수 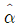 와
와 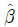 의 값은? (단,
의 값은? (단,  는 각각 x, y의 표본평균이고, εi는 N(0, σ2)을 따르고 서로 독립이다)
는 각각 x, y의 표본평균이고, εi는 N(0, σ2)을 따르고 서로 독립이다)
13. 인자의 수준수가 k이고 각 수준에서의 반복수가 n인 일원배치법에서 얻은 분산분석표의 일부가 다음과 같을 때, 이에 대한 설명으로 옳지 않은 것은?
- 인자의 수준수 k는 4이다.
- 반복수 n은 8이다.
- ㉠의 값은 20이다.
- 인자 수준에 따라 모평균이 같은지를 유의수준 5%에서 검정할 때 모평균은 모두 같다고 할 수 있다.
14. 전체 고등학생이 치른 수학 시험점수는 평균이 60점, 표준편차가 12점인 정규분포를 따른다고 한다. 전체 고등학생 중에서 임의로 뽑은 한 명의 수학 시험점수를 X라 하고, 임의로 뽑은 36명의 수학 시험점수의 표본평균을 Y라 할 때, 이에 대한 설명으로 옳지 않은 것은?
- E(X) = E(Y)
- Var(X) = 2 × Var(Y)
- P(X>60) = P(Y>60)
- P(X<72) = P(Y<62)
15. 정규분포 N(μ, 22)을 따르는 모집단에서 임의추출한 9개 표본의 표본평균이 12 일 때, 가설 H0 : μ = 10 대 H1 : μ ≠ 10 에 대한 p-값과 같은 것은? (단, Z는 표준정규분포를 따르는 확률변수이다)
- 2×P(Z≥3)
- P(Z≥3)
- P(Z≤3)
- 2×P(Z≤3)-1
16. 어느 공장에서 생산되는 제품의 불량률 p에 대한 가설 H0 : p = 0.04 대 H1 : p > 0.04 를 검정하려고 한다. 이 공장에서 임의추출한 384개 제품 중 불량품의 개수를 X라고 하자. 기각역으로 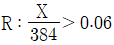 을 사용할 때, 제1종 오류를 범할 확률과 같은 것은? (단, Z는 표준정규분포를 따르는 확률변수이다)
을 사용할 때, 제1종 오류를 범할 확률과 같은 것은? (단, Z는 표준정규분포를 따르는 확률변수이다)
- P(Z>1.5)
- P(Z>2)
- P(Z>2.5)
- P(Z>3)
17. 1부터 13까지의 자연수 중 하나와 4개의 무늬 ♣, ♠, ♥, ♦ 중 하나를 조합하여 각각 적은 같은 크기의 52장의 카드가 있다. 이 52장의 카드에서 임의로 한 장의 카드를 뽑을 때, 이 카드에 ♣ 무늬가 적힌 사건을 A, 숫자 1이 적힌 사건을 B라고 하자. 이에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄱ, ㄹ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ, ㄹ
18. 성공의 확률이 p인 베르누이 시행을 독립적으로 100회 반복할 때 성공 횟수를 확률변수 X라 하자. 이에 대한 설명으로 옳지 않은 것은? (단, 0<p<1)
 이면
이면 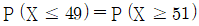 이다.
이다.- X의 분산은
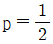 일 때 최댓값을 가진다.
일 때 최댓값을 가진다. 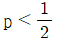 이면
이면 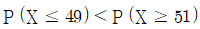 이다.
이다.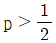 이면
이면 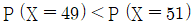 이다.
이다.
19. 분산 σ2이 알려진 정규분포 N(μ, σ2)을 따르는 모집단에서 임의추출한 n개 표본을 이용하여 유의수준 α에서 가설 H0 : μ = μ0 대 H1 : μ ≠ μ0을 검정하려고 한다. 검정통계량이 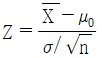 일 때, 이에 대한 설명으로 옳은 것만을 모두 고르면? (단, 0<α<1은 상수이고,
일 때, 이에 대한 설명으로 옳은 것만을 모두 고르면? (단, 0<α<1은 상수이고, 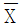 는 표본평균이다)
는 표본평균이다)
- ㄴ
- ㄷ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
20. 한 요인의 3개 수준 A, B, C에서 10회씩 반복 측정한 자료에 대해 요인의 수준에 따라 반응변수 Y의 평균에 차이가 있는지 알아보기 위하여 다음 선형회귀모형을 적합하고자 한다. 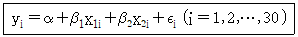
위 모형에서 i번째 자료의 요인의 수준이 A이면 (x1i, x2i) = (0, 0), 요인의 수준이 B이면 (x1i, x2i) = (1, 0), 요인의 수준이 C이면 (x1i, x2i) = (0, 1)이다. 모수 β1 ,β2 의 가설검정 결과에 대한 해석으로 옳은 것은? (단, εi는 N(0, σ2)을 따르고 서로 독립이다)
- 가설 H0 : β1 = 0 대 H1 : β1 ≠ 0에서 H0을 기각하지 못한다면 수준 A와 수준 B의 반응변수의 평균은 유의한 차이가 있다.
- 가설 H0 : β1 = 0 대 H1 : β1 ≠ 0에서 H0을 기각한다면 수준 B와 수준 C의 반응변수의 평균은 유의한 차이가 있다.
- 가설 H0 : β2 = 0 대 H1 : β2 ≠ 0에서 H0을 기각하지 못한다면 수준 B와 수준 C의 반응변수의 평균은 유의한 차이가 없다.
- 가설 H0 : β2 = 0 대 H1 : β2 ≠ 0에서 H0을 기각한다면 수준 A와 수준 C의 반응변수의 평균은 유의한 차이가 있다.






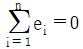 이다."는 옳은 설명이 아닙니다.
이다."는 옳은 설명이 아닙니다.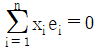 는 t-검정에서 검정통계량으로 사용되는 값으로, 회귀계수의 추정치와 그 표준오차를 이용하여 계산됩니다. 이 값이 크면 회귀계수의 추정치가 표준오차에 비해 유의하게 큰 값이므로, 해당 회귀계수가 유의미한지를 판단하는 데 사용됩니다.
는 t-검정에서 검정통계량으로 사용되는 값으로, 회귀계수의 추정치와 그 표준오차를 이용하여 계산됩니다. 이 값이 크면 회귀계수의 추정치가 표준오차에 비해 유의하게 큰 값이므로, 해당 회귀계수가 유의미한지를 판단하는 데 사용됩니다.