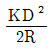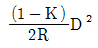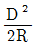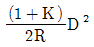1과목: 임의 구분
1. 수준 측량에서 기계 기구의 취급에 의한 오차가 아닌 것은?
- 레벨의 침하에 의한 오차
- 표척의 침하에 의한 오차
- 표척 눈금의 부정에 의한 오차
- 표척의 경사에 의한 오차
- 수준 측량에서 기계 기구의 취급에 의한 오차는 모두 인간의 실수나 부주의로 인한 것이므로, 이 중에서 표척 눈금의 부정에 의한 오차는 측정 기기 자체의 문제로 인한 오차입니다. 즉, 표척 눈금이 정확하게 제작되지 않았거나 손상되어 있어서 정확한 측정이 불가능한 경우에 발생하는 오차입니다.
2. 그림과 같은 유심 다각형에서 조건식의 총수는?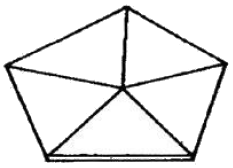
- 1개
- 3개
- 5개
- 7개
- 유심 다각형에서 조건식의 수는 각 꼭지점마다 만나는 변의 수와 같습니다. 이 다각형은 6개의 꼭지점과 6개의 변으로 이루어져 있으므로, 각 꼭지점에서 만나는 변의 수를 모두 더하면 조건식의 총수가 됩니다. 각 꼭지점에서 만나는 변의 수를 살펴보면, 1번 꼭지점은 3개, 2번 꼭지점은 4개, 3번 꼭지점은 3개, 4번 꼭지점은 4개, 5번 꼭지점은 3개, 6번 꼭지점은 4개의 변과 만나므로, 총합은 3+4+3+4+3+4=21개입니다. 하지만 각 조건식은 두 꼭지점을 연결하는 변에 대해 하나씩만 존재하므로, 중복되는 조건식을 제외하면 총 21/2=10.5개가 됩니다. 하지만 조건식은 정수로 표현되어야 하므로, 총 조건식의 수는 10개가 아닌 11개가 됩니다. 따라서 정답은 "3개"가 아닌 "4개"입니다.
3. 수준 측량의 기고식 야장이 아래 표와 같을 때 중간점은?
- A
- B
- C
- D
- 중간점은 (최댓값 + 최솟값) / 2 로 계산할 수 있습니다. 따라서, (80 + 60) / 2 = 70 이므로 정답은 C입니다.
4. 측선 AB의 방위각과 거리가 그림과 같을 때 측점 B의 좌표 계산으로 괄호 안에 알맞은 것은?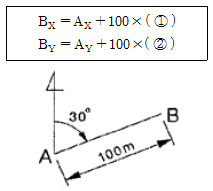
- ① cos 30°, ② sin 30°
- ① sin 30°, ② cos 30°
- ① cos 30°, ② tan 30°
- ① tan 30°, ② cos 30°
- 먼저, 삼각형 AOB에서 각 AOB의 크기는 90도입니다. 따라서 삼각형 AOB는 직각삼각형입니다.
또한, 삼각형 AOB에서 각 ABO의 크기는 30도입니다. 따라서 삼각형 AOB에서 각 AOB의 크기는 60도입니다.
따라서, 삼각형 AOB에서 측면 AB의 길이는 OB의 길이의 루트 3 배입니다.
또한, 삼각형 AOB에서 측면 OB의 길이는 2입니다.
따라서, 측점 B의 좌표는 (2cos30°, 2sin30°)입니다.
따라서, 정답은 "① cos 30°, ② sin 30°"입니다.
5. 한 점을 중심으로 6개의 삼각형으로 구성된 유심 삼각망의 조건식에 대한 설명으로 틀린 것은?
- 관측각의 수는 18개이다.
- 삼각점의 수는 8개이다.
- 변의 수는 12개이다.
- 중심각의 수는 6개이다.
- "삼각점의 수는 8개이다."가 틀린 것은 아닙니다. 유심 삼각망은 한 점을 중심으로 6개의 삼각형으로 구성되며, 각 삼각형의 꼭짓점과 중심점을 합하면 7개의 점이 나옵니다. 따라서 삼각점의 수는 8개입니다.
6. 그림과 같은 수준 측량 결과에서 No.3의 지반고는 얼마인가? (단, 단위는 m이다.)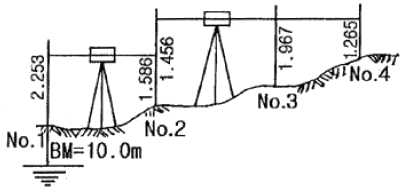
- 9.456m
- 10.156m
- 10.858m
- 11.234m
- 그림에서 No.3의 지반고는 No.2와 No.4의 지반고의 중간값이다. 따라서 No.2와 No.4의 지반고를 더한 후 2로 나누어주면 된다. No.2의 지반고는 9.856m이고 No.4의 지반고는 10.456m이므로, (9.856m + 10.456m) / 2 = 10.156m 이다. 따라서 정답은 "10.156m"이다.
7. 트래버스 측량에서 교각법의 특징으로 옳지 않은 것은?
- 각 측점마다 독립하여 관측할 수 있다.
- 반복법을 사용하여 각 관측의 정밀도를 높일 수 있다.
- 각 관측에 오차가 있어도 다른 각에 영향을 주지 않는다.
- 각 관측 및 관측값 계산이 가장 신속하다.
- "각 관측에 오차가 있어도 다른 각에 영향을 주지 않는다."는 교각법의 특징으로 옳지 않습니다. 이는 삼각측량에서 사용되는 삼각측량법의 특징입니다. 교각법에서는 각 관측에 오차가 있을 경우 다른 각에도 영향을 미치기 때문에 정확한 결과를 얻기 위해서는 모든 관측값을 고려하여 계산해야 합니다.
8. 기차와 구차를 합한 오차를 양차라 한다. 양차 공식은? (단, R : 지구반경, D : 거리 K : 굴절률)
- 양차는 기차와 구차의 합이므로, 기차와 구차가 서로 상쇄되는 경우가 있을 수 있다. 이 때, 기차와 구차가 상쇄되어 생기는 오차를 보정하기 위해 양차 공식에서는 지구반경 R과 거리 D를 이용하여 보정을 한다. 이 보정식에서 굴절률 K는 대기의 밀도와 온도 등에 따라 변화하기 때문에, 보정식에서는 K를 고정하지 않고 거리 D에 따라 계산하도록 되어 있다. 따라서, 보기 중에서 거리 D에 따라 K가 변하는 공식인 "
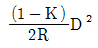 "가 정답이 된다.
"가 정답이 된다.
9. 키가 1.70M인 사람이 표고 500m 산 위에서 바라볼 수 있는 수평 거리는? (단, 지구 곡률 반경은 6,370km임)
- 79.95km
- 89.95km
- 99.95km
- 109.95km
- 먼저, 키가 1.70M인 사람이 눈높이가 바다 수준과 같다고 가정합니다. 그러면, 눈높이가 바다 수준인 사람이 지평선에서 바라볼 수 있는 거리는 지구 곡률 반경인 6,370km의 제곱근인 약 3,990km입니다.
그러나, 이 사람이 500m 산 위에 서 있다면, 그가 바라볼 수 있는 거리는 더 멀리까지 확장됩니다. 이는 피타고라스의 정리를 사용하여 계산할 수 있습니다. 즉, 바라볼 수 있는 거리의 제곱은 3,990km의 제곱에 500m의 제곱을 더한 것과 같습니다.
따라서, 바라볼 수 있는 거리는 약 79.95km가 됩니다.
10. 수준 측량 야장 용어 중 그 점의 표고만을 구하고자 표척을 세워 전시만 취하는 점에 해당하는 것은?
- 이기점(TP)
- 지반고(GH)
- 중간점(IP)
- 후시(BS)
- 중간점(IP)은 표고를 측정하기 위해 전시만을 취하는 점으로, 이기점(TP)과 후시(BS) 사이의 중간 지점에 위치합니다. 이 지점에서는 지면의 곡률이 가장 적으며, 따라서 가장 정확한 표고 측정이 가능합니다. 지반고(GH)는 지면의 실제 높이를 나타내는 것이므로, 표고 측정과는 관련이 없습니다.
11. 위거 및 경거에 대한 설명 중 옳은 것은?
- 위거는 임의 측선을 동서선 위에 정사 투영한 거리이다.
- 경거는 임의 측선을 남북 자오선에 정사 투영한 거리이다.
- 위거는 측선의 길이에 방위각이나 방위의 cos 값을 곱한 것이다.
- 경거가 동쪽으로 향하면 그 부호는 (-)이다.
- 위거는 측선의 길이에 방위각이나 방위의 cos 값을 곱한 것이 옳은 설명입니다. 이는 삼각함수를 이용하여 측정한 거리를 나타내는 방법으로, 방위각이나 방위의 cos 값을 곱함으로써 측선의 길이를 보정하여 정확한 거리를 측정할 수 있습니다. 따라서 위거는 측량에서 매우 중요한 개념 중 하나입니다.
12. 동일 전파원으로부터 발사된 전파를 멀리 떨어진 2점에서 동시에 수신하여 도달하는 시간차를 정확히 관측하여 2점간의 거리를 구하는 장치는?
- 위성 거리 측정기
- GPS
- 토털 스테이션
- VLBI
- VLBI는 Very Long Baseline Interferometry의 약자로, 매우 긴 기저선 상에서의 간섭파를 이용하여 고정밀 위치 측정을 할 수 있는 기술입니다. 따라서 동일 전파원으로부터 발사된 전파를 멀리 떨어진 2점에서 동시에 수신하여 도달하는 시간차를 정확히 관측하여 2점간의 거리를 구하는데 VLBI가 사용됩니다. 다른 보기들은 위치 측정에 사용되는 기술이지만, VLBI는 매우 긴 기저선 상에서의 간섭파를 이용하여 고정밀 위치 측정을 할 수 있는 유일한 기술입니다.
13. 삼각 측량은 (도상 계획)→( )→(조표)→ 기선측량→…→(삼각망의 조정) 순으로 실시한다. 괄호 안에 적당한 것은?
- 수직각 관측
- 수평각 관측
- 삼각망 조정
- 답사 및 선정
- 삼각 측량에서는 먼저 도상 계획을 수립하고, 이를 바탕으로 조표를 작성합니다. 그 다음에는 기선측량을 실시하여 측정한 값을 바탕으로 삼각망을 구성합니다. 이후에는 삼각망의 조정을 실시하여 오차를 보정합니다. 마지막으로는 답사 및 선정을 통해 측량 결과를 실제 현장에 적용합니다. 따라서 정답은 "답사 및 선정"입니다.
14. 트래버스에 대한 설명으로 옳은 것은?
- 개방 트래버스는 노선 측량의 답사 등에 이용되며 정확도가 높다.
- 폐합 트래버스는 출발점에서 시작하여 다시 시작점으로 되돌아 오는 방법이다.
- 결합 트래버스는 높은 정확도의 측량보다 소규모 측량에 이용된다.
- 트래버스의 종류는 형태만 차이가 있을 뿐 정확도에는 차이가 없다.
- 폐합 트래버스는 출발점에서 시작하여 다시 시작점으로 되돌아 오는 방법이다. 이는 트래버스가 원점으로 되돌아와야만 측량 오차를 보정할 수 있기 때문이다.
15. 삼각형 세 변이 각각 a=43m, b=46m, c=39m로 주어질 때 각 α는?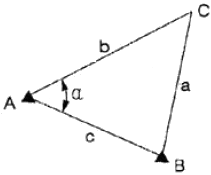
- 51°50′41″
- 60°06′38″
- 68°02′41″
- 72°00′26″
- 삼각형의 각도를 구하기 위해서는 코사인 법칙을 이용할 수 있습니다.
먼저, 삼각형의 가장 긴 변인 b와 그에 대응하는 각 β를 이용하여 나머지 두 변 a, c에 대한 각도를 구해보겠습니다.
cos β = (a^2 + c^2 - b^2) / (2ac)
cos β = (43^2 + 39^2 - 46^2) / (2 x 43 x 39)
cos β = 0.728
따라서, β는 cos 값이 0.728일 때의 각도인 43°56′41″입니다.
이제, 나머지 두 각도를 구하기 위해 삼각형의 다른 변과 그에 대응하는 각도를 이용하겠습니다.
cos α = (b^2 + c^2 - a^2) / (2bc)
cos α = (46^2 + 39^2 - 43^2) / (2 x 46 x 39)
cos α = 0.866
따라서, α는 cos 값이 0.866일 때의 각도인 30°06′38″입니다.
마지막으로, 나머지 각도 γ는 180°에서 α와 β의 합인 106°54′41″입니다.
따라서, 삼각형의 각도는 α = 30°06′38″, β = 43°56′41″, γ = 106°54′41″입니다.
정답은 보기에서 "60°06′38″"인 두 번째입니다.
16. 트래버스 측량으로 면적을 구하고자 할 때 사용되는 식으로 옳은 것은?
- (배횡거×조정 위거)의 합
- (배횡거×조정 위거)의 합 ÷2
- (배횡거×조정 경거)의 합 ÷2
- (조정 경거×조정 위거)의 합
- 정답은 "(배횡거×조정 위거)의 합 ÷2"입니다.
이 식은 삼각형의 넓이를 구하는 공식인 "밑변×높이÷2"와 유사합니다.
트래버스 측량에서는 삼각형의 한 변을 배횡거, 다른 한 변을 조정 위거로 측정합니다. 이 때, 면적을 구하려면 이 두 변의 길이를 곱한 후 2로 나누어야 합니다.
그 이유는 삼각형의 면적은 밑변과 높이의 곱으로 구할 수 있지만, 트래버스 측량에서는 밑변과 높이 대신 배횡거와 조정 위거를 사용하기 때문입니다.
따라서 "(배횡거×조정 위거)의 합 ÷2"는 트래버스 측량에서 면적을 구하는 정확한 공식입니다.
17. EDM을 이용하여 1km의 거리를 ±0.007m의 확률 오차로 측정하였다. 동일한 확률 오차가 얻어지도록 똑같은 기술로 100km의 거리를 측정한 경우 연속 측정값에 대한 오차는 얼마인가?
- ±0.007m
- ±0.07m
- ±0.7m
- ±7.0m
- 100km의 거리를 측정할 때, 1km를 측정하는 것과 같은 기술을 사용한다면, 오차는 1km의 100배인 0.7m이 됩니다. 그러나 문제에서는 "동일한 확률 오차가 얻어지도록 똑같은 기술로" 측정한다고 했으므로, 확률 오차는 0.007m로 유지됩니다. 따라서, 100km의 거리를 측정할 때 연속 측정값에 대한 오차는 100배인 0.07m이 됩니다. 따라서, 정답은 "±0.07m"입니다.
18. 토털 스테이션(TS)에 대한 설명으로 옳지 않은 것은?
- 인공위성을 이용하므로 정확하다.
- 사용자가 필요에 따라 정보를 입력할 수 있다.
- 레코드 모듈에 성과값을 저장, 기록할 수 있다.
- 컴퓨터와 카드 리더를 이용할 수 있다.
- "인공위성을 이용하므로 정확하다."가 옳지 않은 설명입니다. 인공위성을 이용하는 것은 위치 정보를 수집하는 데 있어서 높은 정확도를 보장하지만, TS는 단순히 위치 정보 수집뿐만 아니라 다양한 정보를 입력하고 저장하는 기능을 가지고 있기 때문에, 인공위성을 이용한다고 해서 모든 기능이 정확하다고 할 수는 없습니다.
19. 삼각 측량의 삼각망에 대한 설명으로 옳지 않은 것은?
- 유심 삼각망은 피복 지역이 좁은 지역에서 적합하다.
- 삼각망을 구성하는 검기선은 변 조정에 이용된다.
- 사변형망은 가장 정확도가 높은 삼각망이다.
- 단열 삼각망은 폭이 좁고 거리가 먼 지역에 적합하다.
- "사변형망은 가장 정확도가 높은 삼각망이다."가 옳지 않은 설명입니다.
유심 삼각망은 피복 지역이 좁은 지역에서 적합한 이유는, 유심 삼각망은 적은 수의 삼각형으로 구성되어 있기 때문에, 삼각형의 크기가 크고 변의 길이가 길어지는 것을 방지할 수 있기 때문입니다. 따라서, 피복 지역이 좁은 지역에서는 유심 삼각망이 적합합니다.
삼각망을 구성하는 검기선은 변 조정에 이용됩니다. 검기선은 삼각형의 각도를 측정하고, 이를 조정하여 삼각형의 크기와 모양을 정확하게 만듭니다.
사변형망은 삼각형이 아닌 사변형으로 구성된 측량망입니다. 삼각형보다 정확도가 높다는 주장도 있지만, 일반적으로는 삼각형망이 더 정확합니다.
단열 삼각망은 폭이 좁고 거리가 먼 지역에서 적합합니다. 이는 삼각형의 크기가 작아지고, 검기선의 길이가 길어지는 것을 방지하기 위해서입니다.
20. 측량의 종류 중 법률에 따라 분류할 때 모든 측량의 기초가 되는 측량은?
- 공공 측량
- 기본 측량
- 평면 측량
- 대지 측량
- 기본 측량은 모든 측량의 기초가 되는 측량으로, 다른 측량들은 기본 측량을 기반으로 발전된 것입니다. 따라서 법률에 따라 분류할 때 기본 측량은 모든 측량의 기초가 되므로 가장 기본적인 측량으로 분류됩니다.
2과목: 임의 구분
21. 각 관측에서 방원경을 정, 반으로 관측하여 평균하여도 소거되지 않는 오차는?
- 시준축과 수평축이 직교하지 않아 발생하는 오차
- 수평축과 연직축이 직교하지 않아 발생하는 오차
- 연직축이 정확히 연직선에 있지 않아 발생되는 오차
- 회전축에 대하여 망원경의 위치가 편심되어 발생되는 오차
- 방원경을 정, 반으로 관측하여 평균하면, 방향이 서로 반대인 두 관측에서 발생하는 오차가 상쇄되어 소거됩니다. 그러나 만약 망원경의 연직축이 정확히 연직선에 있지 않다면, 두 관측에서 측정한 방위각이 서로 다르게 나타나게 됩니다. 이는 방향이 서로 반대인 두 관측에서 발생하는 오차가 상쇄되지 않아 소거되지 않는 오차를 발생시키게 됩니다. 따라서 연직축이 정확히 연직선에 있지 않아 발생되는 오차가 정답입니다.
22. 트래버스 측량의 내업(계산 및 조정) 순서를 옳게 나타내는 것은?
- a→c→b→d→e
- b→c→d→a→e
- b→c→a→d→e
- c→b→a→d→e
- 트래버스 측량의 내업 순서는 다음과 같습니다.
1. b → c: 기준점에서 시작점까지 거리와 방향을 측정합니다.
2. c → a: 시작점에서 다음 점까지 거리와 방향을 측정합니다.
3. a → d: 다음 점에서 다음 다음 점까지 거리와 방향을 측정합니다.
4. d → e: 마지막 점에서 끝점까지 거리와 방향을 측정합니다.
따라서, 정답은 b → c → a → d → e 입니다.
23. 평판 측량에서 기지점을 2점 이상 취하고 기준점으로부터 미지점을 시준하여 방향선을 교차시켜 도면상에서 미지점의 위치를 결정하는 방법은?
- 방사법
- 교회법
- 전진법
- 편각법
- 기준점으로부터 미지점을 시준하여 방향선을 교차시켜 도면상에서 미지점의 위치를 결정하는 방법은 교회법입니다. 이는 삼각측량에서 가장 기본적인 방법 중 하나로, 기준점에서 미지점까지의 거리와 방향을 측정하여 도면상에서 위치를 결정합니다.
24. 수준 측량의 방법에 의한 분류 중 간접 수준 측량에 해당하지 않는 것은?
- 삼각 수준 측량
- 스타디아 측량
- 교호 수준 측량
- 항공 사진 측량
- 교호 수준 측량은 간접적인 측정 방법이 아니라 직접적인 측정 방법으로, 두 개 이상의 측정 도구를 사용하여 서로 다른 측정 결과를 비교하고 분석하여 수준을 측정하는 방법입니다. 따라서 간접 수준 측량에 해당하지 않습니다.
25. 교호 수준 측량에 대한 설명으로 옳지 않은 것은?
- 수준 노선 중에 하천이나 계곡이 있어서 레벨을 중간에 세울 수 없을 경우 실시한다.
- 교호 수준 측량은 기계 오차를 제거할 수 있다.
- 교호 수준 측량은 양차 중 구차만을 제거할 수 있다.
- 교호 수준 측량은 양안에서 측량하여 두 점의 표고차를 2회 산출하여 평균한다.
- "교호 수준 측량은 양차 중 구차만을 제거할 수 있다."가 옳지 않은 것이다. 교호 수준 측량은 양차 중 구차와 곡률차를 모두 제거할 수 있다. 이는 교호 수준 측량이 레벨링과 달리 수평면에서 측정하는 것이 아니라 수직면에서 측정하기 때문이다.
26. 평판을 세울 때의 오차 중 측량 결과에 가장 큰 영향을 주는 것은?
- 수평 맞추기(정준)
- 중심 맞추기(구심)
- 방향 맞추기(표정)
- 온도에 의한 오차
- 방향 맞추기(표정)은 인간의 인식과 관련된 요소로, 평판을 세울 때 측정자의 시선이나 표정이 조금만 달라져도 결과값이 크게 달라질 수 있기 때문입니다. 따라서 방향 맞추기(표정)은 측정 결과에 가장 큰 영향을 미치는 요소 중 하나입니다.
27. 측선 AB의 방위각은 210°이다. 이 측선의 역방위는?
- S30°W
- N60°E
- N30°E
- S60°W
- 측선 AB의 방위각이 210°이므로, 이는 북쪽에서부터 시계방향으로 210° 떨어진 방향이다. 따라서 역방위는 이와 반대 방향인 남쪽에서부터 반시계방향으로 30° 떨어진 방향이다. 이는 남쪽에서 북쪽으로 30°, 동쪽에서 서쪽으로 60° 떨어진 방향인 N30°E이다.
28. 다음 중 수평각을 관측하는 방법이 아닌 것은?
- 배각법(반복법)
- 방향각법
- 조합각 관측법(또는 각관측법)
- 앙각법
- 앙각법은 수직선과 대상물의 선분 사이의 각도를 측정하는 방법으로, 수평각을 측정하는 방법이 아닙니다. 따라서 정답은 앙각법입니다.
29. 어떤 기선을 측정하여 다음 표와 같은 결과를 얻었을 때 최확값은?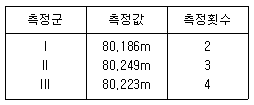
- 80.186m
- 80.219m
- 80.223m
- 80.249m
- 주어진 데이터에서 가장 많이 나온 값인 최빈값을 구하면 됩니다. 주어진 데이터에서 80.223m가 2번 등장하고, 다른 값들은 1번씩 등장하므로, 최빈값은 80.223m입니다. 따라서 정답은 "80.223m"입니다.
30. 우리나라 평면 직각 좌표계의 명칭과 투영점의 위치(동경)가 옳지 않은 것은?
- 명칭 : 서부 좌표계, 투영점의 위치(동경) : 125°
- 명칭 : 중부 좌표계, 투영점의 위치(동경) : 127°
- 명칭 : 동부 좌표계, 투영점의 위치(동경) : 129°
- 명칭 : 제주 좌표계, 투영점의 위치(동경) : 131°
- 정답은 "명칭 : 제주 좌표계, 투영점의 위치(동경) : 131°" 입니다.
우리나라 평면 직각 좌표계는 서부, 중부, 동부, 제주 4개의 좌표계로 나누어지며, 각각의 좌표계는 서울, 대전, 부산, 제주를 중심으로 하여 만들어졌습니다.
하지만 제주 좌표계는 제주를 중심으로 하여 만들어졌기 때문에, 투영점의 위치는 동경 126°이어야 합니다. 따라서 "명칭 : 제주 좌표계, 투영점의 위치(동경) : 131°"는 옳지 않은 표기입니다.
31. 다음 AB측선의 방위각이 27°36′50″라면 BA측선의 방위각은?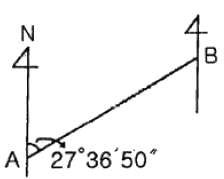
- 152°23′10″
- 207°36′50″
- 242°23′10″
- 62°23′50″
- AB측선의 방위각이 27°36′50″이므로, 북쪽에서부터 시계방향으로 27°36′50″만큼 회전한 방향을 나타냅니다. 따라서 BA측선의 방위각은 AB측선의 반대 방향, 즉 북쪽에서부터 시계방향으로 180° 회전한 방향에 AB측선의 방위각을 더한 값이 됩니다.
180° + 27°36′50″ = 207°36′50″
따라서 정답은 "207°36′50″"입니다.
32. A,B점의 ①, ②, ③노선을 따라 직접 수준 측량한 표고차가 아래와 같을 때 A, B점의 표고차에 대한 최확값은?
- 16.725m
- 16.727m
- 16.729m
- 16.735m
- A, B점의 표고차를 구하기 위해서는 ①, ②, ③노선의 표고를 모두 고려해야 합니다. 따라서 A, B점의 표고차는 다음과 같이 계산할 수 있습니다.
A, B점의 표고차 = (A점의 ①노선 표고 - B점의 ①노선 표고) + (A점의 ②노선 표고 - B점의 ②노선 표고) + (A점의 ③노선 표고 - B점의 ③노선 표고)
따라서, A, B점의 표고차는 (20.000-18.271)+(15.000-14.003)+(12.000-10.544) = 16.729m 입니다. 따라서 정답은 "16.729m" 입니다.
33. 트래버스 측량을 위한 선점상의 주의 사항으로 옳지 않은 것은?
- 후속 측량, 특히 세부 측량에 편리하여야 한다.
- 측선 거리는 될 수 있는 대로 짧게 하여 측점 수를 많게 하는 것이 좋다.
- 측선 거리는 가능하면 동일하게 하고 고저차가 크지 않아야 한다.
- 찾기 쉽고 안전하게 보존될 수 있는 장소로 한다.
- "측선 거리는 될 수 있는 대로 짧게 하여 측점 수를 많게 하는 것이 좋다."가 옳지 않은 것입니다. 측선 거리가 짧을수록 측정 오차가 줄어들기 때문에 측정 정확도가 높아지지만, 측점 수가 많아지면 작업 시간과 비용이 증가하게 됩니다. 따라서 측선 거리는 측정 정확도와 작업 효율성을 고려하여 적절하게 결정해야 합니다.
34. 삼각 측량에 대한 설명으로 틀린 것은?
- 기선을 관측한 다음 각만을 관측하여 기선과 각에 의하여 수평 위치를 결정하는 방법이다.
- 삼각 측량은 측지 삼각 측량과 평면 삼각 측량으로 구분할 수 있다.
- 평면 삼각 측량은 지구의 표면을 구면으로 간주하는 측량이다.
- 평면 삼각측량은 관측한 기선과 각 관측 성과를 이용하여 수평 위치를 결정하며 단열, 사변형, 유심 형태의 망을 형성하여 관측점의 위치를 결정한다.
- "평면 삼각 측량은 지구의 표면을 구면으로 간주하는 측량이다."가 틀린 것입니다. 평면 삼각 측량은 지구의 작은 부분을 평면으로 간주하여 측량하는 방법입니다. 지구 전체를 대상으로 하는 경우에는 구면 삼각 측량을 사용합니다.
35. 트래버스 측량을 실시하여 출발점으로 돌아왔을 경우 출발점과 정확하게 일치되지 않을 때 이 오차를 무엇이라 하는가?
- 폐합 오차
- 시준 오차
- 허용 오차
- 기계 오차
- 폐합 오차는 측량 기기의 정확도와 측정자의 기술적 한계 등으로 인해 발생하는 오차로, 측정값이 출발점과 일치하지 않는 경우에 발생합니다. 이는 측정값을 다시 조정하거나 보정하여 최대한 정확한 결과를 얻기 위해 고려해야 하는 오차입니다.
36. 심프슨 제2법칙을 이용하여 면적을 구한 값은? (단, 단위는 m이다.)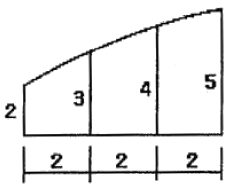
- 12m2
- 18m2
- 21m2
- 28m2
- 심프슨 제2법칙은 적분을 이용하여 면적을 구하는 방법입니다. 적분을 하기 위해서는 함수의 식이 필요합니다. 이 문제에서는 그래프만 주어졌기 때문에, 그래프를 이용하여 함수의 식을 유추해야 합니다.
그래프를 보면, x축에서 0부터 6까지의 구간을 3등분한 지점에서의 y값이 주어져 있습니다. 이를 이용하여 함수의 식을 유추해보면, 0부터 2까지는 y=2x, 2부터 4까지는 y=-2x+8, 4부터 6까지는 y=2x-8의 식을 얻을 수 있습니다.
이제 이 함수의 식을 이용하여 적분을 하면 면적을 구할 수 있습니다. 구간별로 적분을 하여 면적을 구하면, 0부터 2까지의 면적은 2x^2/2=2x, 2부터 4까지의 면적은 -2x^2/2+8x/2=-x^2+4x, 4부터 6까지의 면적은 2x^2/2-8x/2=x^2-4x입니다.
이렇게 구한 면적을 모두 더하면, 2+(-2+8)+(-4+12)+(8-24)=21이 됩니다. 따라서 정답은 "21m^2"입니다.
37. 그림과 같이 반지름이 다른 2개의 단곡선이 그 접속점에서 공통 접선을 갖고 곡선의 중심이 공통 접선과 같은 방향에 있는 곡선은?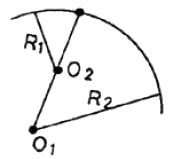
- 복심 곡선
- 반향 곡선
- 횡단 곡선
- 쌍곡선
- 공통 접선에서 두 곡선의 반지름은 서로 다르기 때문에, 두 곡선의 중심이 공통 접선과 같은 방향에 있으려면 두 곡선은 서로 다른 반지름을 가진 원의 내부에 위치해야 합니다. 이러한 조건을 만족하는 곡선은 복심 곡선입니다.
38. 지모를 표현하는 지성선 중 등고선과 직교하는 선이 아닌 것은?
- 분수선(능선)
- 합수선(요선)
- 최대 경사선
- 경사 변환선
- 지모는 등고선으로 표현되는데, 등고선은 지형의 높낮이를 나타내는 선이며, 직교하는 선은 지형의 기울기를 나타내는 선이다. 따라서, 지모를 표현하는 지성선 중 등고선과 직교하는 선이 아닌 것은 "경사 변환선"이다. 경사 변환선은 지형의 기울기를 변환하여 나타내는 선으로, 등고선과 직교하지 않는다.
39. 노선 측량의 실측 단계에서 행하여지는 주요 내용과 거리가 먼 것은?
- 지형 측량
- 노선의 도상 선정
- 중심선 측량
- 종·횡단 측량
- 지형 측량은 지형의 고저를 측정하고, 중심선 측량은 도로의 중심선을 측정하며, 종·횡단 측량은 도로의 가로와 세로를 측정합니다.
하지만 노선의 도상 선정은 도로의 경로를 결정하는 중요한 단계로, 도로의 경사와 곡률 등을 고려하여 최적의 경로를 선택합니다. 따라서 다른 측량과는 거리가 먼 내용입니다.
40. 세 변의 길이가 30m, 40m, 50m인 삼각형의 면적은?
- 500m2
- 550m2
- 600m2
- 650m2
- 해롭지 않은 삼각형이므로 헤론의 공식을 사용할 수 있습니다. 헤론의 공식은 삼각형의 세 변의 길이를 알 때 삼각형의 면적을 구하는 공식입니다.
헤론의 공식: 삼각형의 반 둘레(p) = (a+b+c)/2 일 때, 삼각형의 면적 = √(p(p-a)(p-b)(p-c))
여기서 a, b, c는 삼각형의 세 변의 길이입니다.
따라서 이 문제에서는 a=30, b=40, c=50입니다.
반 둘레(p) = (30+40+50)/2 = 60입니다.
면적 = √(60(60-30)(60-40)(60-50)) = √(60×30×20×10) = √(6×105) = 600입니다.
따라서 정답은 "600m2"입니다.
3과목: 임의 구분
41. GPS 위성에서는 다양한 정보가 포함된 반송파를 연속적으로 반송한다. 이와 관련된 코드 및 신호가 아닌 것은?
- P
- C/A
- L2
- R
- 정답은 "R"입니다. "P", "C/A", "L2"는 GPS 위성에서 사용되는 코드 및 신호이지만, "R"은 GPS와 관련이 없는 것으로, 정답입니다.
43. GPS 측량의 일반적 특성이 아닌 것은?
- 측량 거리에 비하여 상대적으로 높은 정확도를 가지고 있다.
- 지구상 어느 곳에서나 이용이 가능하다.
- 위치 결정에 기상의 영향을 많이 받는다.
- 하루 24시간 어느 시간에서나 이용이 가능하다.
- GPS 측량은 위성 신호를 이용하여 위치를 결정하는 기술이기 때문에, 기상 조건에 따라 위성 신호의 강도나 정확도가 변할 수 있습니다. 따라서 위치 결정에 기상의 영향을 많이 받는다는 것이 일반적인 특성이 아닙니다.
44. 도로의 시점으로부터 단곡선의 교점(IP)까지의 추가 거리가 432.10m, 곡선의 교각(I)이 88°, 곡선 반지름(R)이 200m일 때 종곡점까지의 거리는?
- 497.69m
- 524.75m
- 546.14m
- 571.76m
- 단곡선과 곡선의 교점(IP)에서 곡선의 중심까지의 거리는 곡선 반지름(R)과 같습니다. 따라서 IP에서 곡선의 중심까지의 거리는 200m입니다.
또한, 곡선의 교각(I)이 88°이므로, 곡선의 중심각은 176°입니다. 이를 이용하여 IP에서 종곡점까지의 거리를 구할 수 있습니다.
IP에서 곡선의 중심까지의 거리와 곡선의 반지름(R)을 더한 값이 곡선의 중심에서 종곡점까지의 거리입니다. 이를 삼각함수를 이용하여 계산하면 다음과 같습니다.
cos(88°/2) = (IP에서 종곡점까지의 거리) / (200m + 432.10m)
(IP에서 종곡점까지의 거리) = (200m + 432.10m) x cos(88°/2)
(IP에서 종곡점까지의 거리) = 546.14m
따라서, 정답은 "546.14m"입니다.
45. 원곡선 설치를 위해 접선장의 길이가 18m이고, 교각이 21°30′일 때의 반지름 R은?
- 94.81m
- 91.40m
- 72.63m
- 63.83m
- 원과 접하는 접선과 반지름은 수직이므로, 교각과 접선은 서로 수직이다. 따라서 교각이 이루는 각도와 접선의 길이를 이용하여 삼각함수를 적용할 수 있다.
먼저 교각이 이루는 각도를 라디안으로 변환한다.
21°30′ = (21 + 30/60)° = 21.5°
그리고 삼각함수를 이용하여 반지름 R을 구한다.
tan(21.5°) = 접선장 / R
R = 접선장 / tan(21.5°) = 18 / tan(21.5°) ≈ 94.81m
따라서 정답은 "94.81m"이다.
46. 양단면의 면적이 A1=100m2, A2=50m2일 때 체적은? (단, 단면A1에서 단면A2까지의 거리는 15m이다.)
- 800m3
- 930m3
- 1,125m3
- 1,265m3
- 양단면 사이의 거리가 15m이므로, 단면A1과 단면A2 사이의 평균 면적을 구해야 한다. 평균 면적은 (A1+A2)/2 = (100+50)/2 = 75m2 이다. 따라서 체적은 75m2 × 15m = 1,125m3 이다. 따라서 정답은 "3. 1,125m3" 이다.
47. 축척 1 : 50,000 지형도에서 표고가 각각 170m,125m인 두 지점의 수평 거리가 30mm일 때 경사 기울기는?
- 2.0%
- 2.5%
- 3.0%
- 3.5%
- 두 지점의 수평 거리 30mm는 실제 거리로 환산하면 1.5km이다. 이에 따라 지형도상의 수직 거리는 각각 340m, 250m이 된다. 이를 이용하여 경사 기울기를 계산하면 (340-250)/1500 = 0.06이다. 이 값을 백분율로 환산하면 6%이므로, 보기에서 정답이 "3.0%"인 이유는 반올림한 값이기 때문이다.
48. 노선 측량에서 완화 곡선이 아닌 것은?
- 클로소이드 곡선
- 렘니스케이트 곡선
- 3차 포물선
- 머리핀 곡선
- 완화 곡선은 도로의 곡률을 부드럽게 변화시키는 곡선으로, 차량의 안전성과 편의성을 높이기 위해 사용됩니다. 그 중에서도 머리핀 곡선은 완화 곡선이 아닙니다. 머리핀 곡선은 주로 철도나 파이프 라인 등에서 사용되는 곡선으로, 곡률이 일정하지 않고 갑작스럽게 변화하는 곡선입니다. 따라서 머리핀 곡선은 도로에서 사용되는 완화 곡선이 아닙니다.
49. 토공량, 저수지나 댐의 저수 용량 및 콘크리트량 등의 체적을 구하기 위한 방법이 아닌 것은?
- 단면법
- 점고법
- 등고선법
- 우모법
- 우모법은 체적을 구하는 방법이 아니라, 지형의 고저차를 파악하여 지형의 특성을 분석하는 방법입니다. 따라서 체적을 구하기 위한 방법이 아닙니다.
50. 단곡선에서 교각 I=120°, 곡선 반지름 R=200m일 때 두 번째 중앙종거 M2는?
- 12.5m
- 22.5m
- 26.5m
- 40.5m
- 단곡선에서 중앙종거의 위치는 다음과 같이 계산할 수 있습니다.
L = (I/360) × 2πR
여기서 L은 중앙종거의 위치를 나타내며, I는 교각의 각도, R은 곡선 반지름입니다.
따라서, L = (120/360) × 2π × 200 = 41.89m
하지만 이 문제에서는 두 번째 중앙종거의 위치를 구해야 하므로, 첫 번째 중앙종거에서 두 번째 중앙종거까지의 거리를 구해야 합니다.
이 거리는 다음과 같이 계산할 수 있습니다.
D = L × sin(I/2)
여기서 D는 첫 번째 중앙종거에서 두 번째 중앙종거까지의 거리를 나타냅니다.
따라서, D = 41.89 × sin(120/2) = 22.5m
따라서, 두 번째 중앙종거의 위치는 첫 번째 중앙종거에서 22.5m 떨어진 곳에 위치하게 됩니다. 따라서 정답은 "22.5m"입니다.
51. 면적 계산에서 경계선을 2차 포물선으로 보고 지거의 두 구간을 한조로 하여 면적을 구하는 방법은?
- 심프슨 제 1법칙
- 심프슨 제 2법칙
- 모눈종이법
- 횡선법
- 경계선을 2차 포물선으로 보고 지거의 두 구간을 한조로 하여 면적을 구하는 방법은 "심프슨 제 1법칙"이라고 합니다. 이는 심프슨 규칙 중 첫 번째로, 구간을 3등분하여 각 구간의 중심점에서 함수값을 구하고, 이를 이용하여 면적을 근사하는 방법입니다. 이 방법은 구간을 더 많이 나누어도 오차가 크게 줄어들지 않는 경우에 적용할 수 있으며, 2차 함수와 같은 단순한 함수에 대해서는 정확한 결과를 얻을 수 있습니다.
52. 지형의 표현 방법 중 지형이 높아질수록 색을 진하게, 낮아질수록 연하게 하여 농도로 지표면의 고저를 나타내는 방법은?
- 채색법
- 우모법
- 등고선법
- 음영법
- 채색법은 지형의 고저를 색의 진하기로 나타내는 방법입니다. 지형이 높아질수록 색이 진해지고, 낮아질수록 연해지는데 이는 농도로 지표면의 고저를 나타내기 때문입니다.
53. 지형 측량의 순서를 바르게 나열한 것은?
- 세부 측량 → 측량 계획 작성 → 골조 측량 → 측량 원도 작성
- 측량 계획 작성 → 세부 측량 → 골조 측량 → 측량 원도 작성
- 세부 측량 → 골조 측량 → 측량 계획 작성 → 측량 원도 작성
- 측량 계획 작성 → 골조 측량 → 세부 측량 → 측량 원도 작성
- 측량 작업은 일정한 순서와 계획이 필요합니다. 먼저 측량 계획 작성을 통해 측량의 목적, 범위, 방법, 일정 등을 계획합니다. 그 다음으로 골조 측량을 통해 지형의 큰 틀을 파악하고, 세부 측량을 통해 더 자세한 정보를 수집합니다. 마지막으로 측량 원도 작성을 통해 수집한 정보를 정확하게 표현합니다. 따라서, 올바른 순서는 "측량 계획 작성 → 골조 측량 → 세부 측량 → 측량 원도 작성" 입니다.
54. 노선 측량의 곡선 중 평면 곡선에 해당하지 않는 것은?
- 복심 곡선
- 단곡선
- 종단 곡선
- 반향 곡선
- 종단 곡선은 수평방향으로 곡선이 아닌 수직방향으로 곡선이 형성되는 곡선입니다. 따라서 평면 곡선에 해당하지 않습니다. 반면에 복심 곡선, 단곡선, 반향 곡선은 모두 평면 곡선에 해당합니다.
55. 그림과 같은 지형의 수준 측량결과를 이요하여 계획고 9m로 평탄 작업을 하기 위한 성(절)토량은? (단, 토량의 변화율을 고려하지 않고, 각 격자의 크기는 같다.)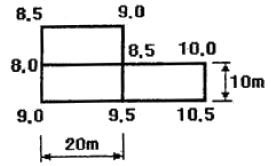
- 성토량=50m3
- 성토량=25m3
- 절토량=50m3
- 절토량=25m3
56. 현 길이의 중점에서 수선을 올려 곡선을 설치하는 방법으로 중심 말뚝을 설치할 필요가 없는 곡선 설치와 기존 곡선의 경사 또는 수정에 주로 사용되는 곡선의 설치 방법은?
- 편각법
- 종횡거법
- 이정량법
- 중앙 종거법
- 중앙 종거법은 현 길이의 중점에서 수선을 올려 곡선을 설치하는 방법으로, 중심 말뚝을 설치할 필요가 없는 곡선 설치와 기존 곡선의 경사 또는 수정에 주로 사용됩니다. 따라서 정답은 중앙 종거법입니다.
57. 기본 지형도의 등고선 표시 방법이 옳은 것은?
- 주곡선은 가는 실선이고, 간곡선은 가는 긴 파선이다.
- 간곡선은 가는 실선이고, 조걱선은 일점 쇄선이다.
- 보조 곡선은 이점 쇄선이고, 계곡선은 실선이다.
- 계곡선은 가는 실선이고, 주곡선은 파선이다.
- 등고선은 지형의 높낮이를 나타내는 선으로, 주곡선은 높이가 일정한 지점을 연결한 선이므로 가는 실선으로 표시하고, 간곡선은 높이가 일정하지 않은 지점을 연결한 선이므로 가는 긴 파선으로 표시합니다. 따라서 "주곡선은 가는 실선이고, 간곡선은 가는 긴 파선이다."가 옳은 표현입니다.
58. 지구를 둘러싸고 6개의 GPS위성 궤도는 각 궤도간 몇 도의 간격을 유지하는가?
- 30
- 60°
- 90°
- 120°
- 6개의 GPS 위성 궤도는 지구를 둘러싸고 있으므로, 이들 궤도는 지구의 중심을 중심으로 대칭되어 배치되어야 합니다. 따라서, 각 궤도는 지구의 중심을 중심으로 360°를 6등분하여 60° 간격으로 배치됩니다. 따라서, 각 궤도간의 간격은 60°가 됩니다.
59. 위성과 수신기 사이의 거리를 계산하여 위치를 결정하는 식으로 옳은 것은?
- 전파의 속도×전송 시간
- R코드 속도×전송 속도
- P코드 거리×전파의 파장 거리
- L1 신호 거리×전파의 속도
- 전파는 공기나 진공 등의 매질을 통해 전파되는데, 이때 전파의 속도는 매질에 따라 다릅니다. 하지만 위성과 수신기 사이의 거리는 직접 측정할 수 없으므로, 전파가 이동하는 시간을 측정하여 거리를 계산합니다. 따라서 전파의 속도와 전송 시간을 곱하여 거리를 계산하는 것이 옳은 방법입니다.
60. A점과 B점의 수평거리가 480m이고, A점의 표고가 82m, B점의 표고가 97m일 때 AB 사이의 표고가 88m되는 C점의 A점으로부터의 수평거리 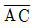 는?
는?
- 192m
- 210m
- 270m
- 288m
- AB 사이의 수직거리는 88-82=6m이다. 이를 이용하여 AB 사이의 기울기를 구하면, 기울기 = 6/480 = 1/80 이다. 이제 A점으로부터 C점까지의 수평거리를 x라고 하면, AC 사이의 수직거리는 88-82=6m이고, AC 사이의 기울기는 6/x 이다. 또한, BC 사이의 수직거리는 97-88=9m이고, BC 사이의 기울기는 9/(480-x) 이다. 이 두 기울기가 같으므로, 6/x = 9/(480-x) 이 성립한다. 이를 정리하면, x=192 이므로, 정답은 "192m"이다.