1과목: 수학
2. 다항식 f(x)를 x-1로 나누었을 때의 몫이 Q(x)이고 나머지가 3이다. Q(x)를 x+1로 나눈 나머지가 –2일 때, f(x)를 x+1로 나눈 나머지의 값은?
- 4
- 5
- 6
- 7
- 다항식 나눗셈에서, 나머지는 나누는 다항식의 차수보다 작은 차수의 다항식이다. 따라서, x-1로 나눈 나머지가 3이므로, f(x)는 (x-1)과 3의 합으로 나타낼 수 있다. 즉, f(x) = (x-1)Q(x) + 3이다.
또한, Q(x)를 x+1로 나눈 나머지가 -2이므로, Q(x)는 (x+1)과 -2의 합으로 나타낼 수 있다. 즉, Q(x) = (x+1)R(x) - 2이다.
따라서, f(x)를 x+1로 나눈 나머지는 다음과 같이 계산할 수 있다.
f(x) = (x-1)Q(x) + 3
= (x-1)((x+1)R(x) - 2) + 3
= (x-1)(x+1)R(x) - 2(x-1) + 3
= (x^2 - 1)R(x) + 1
따라서, f(x)를 x+1로 나눈 나머지는 1이다. 따라서, 정답은 "7"이 아니라 "6"이다.
3. 창식은 영어 모의시험에 총 6회 응시한다. 5번째까지 시험성적의 평균이 83점이었다. 전체 평균이 85점 이상이 되려면, 창식은 6번째 모의시험에서 최소한 몇 점 이상을 받아야 하는가?
- 94점
- 95점
- 96점
- 97점
- 5번째까지의 평균이 83점이므로, 5번째까지의 총 점수는 83 x 5 = 415점이다. 전체 6회의 평균이 85점 이상이 되려면, 6번째 시험에서 받아야 할 점수는 (6 x 85) - 415 = 95점 이상이어야 한다. 따라서 정답은 "95점"이다.
5. x3=1의 한 허근을 ω라 할 때, 1+ω+ω2+ω3+ω4+…+ω2014+ω2015을 간단히 하면?
- 0
- 1
- ω
- 1+ω
- 우선 x3=1의 해는 1, -1/2+√3/2i, -1/2-√3/2i 이다. 여기서 ω는 -1/2+√3/2i 이다.
그러면 1+ω+ω2+ω3+ω4+…+ω2014+ω2015은 어떻게 될까?
우선 ω3=1 이므로, ω4=ω, ω5=ω2, ω6=1, ω7=ω, ω8=ω2, ... 이렇게 반복된다.
따라서 1+ω+ω2+ω3+ω4+…+ω2014+ω2015은 1+ω+ω2+1+ω+ω2+... 이렇게 반복되므로, 2016개의 항 중 2개씩 묶어서 더하면 1008개의 2로 묶인 항이 나오고, 이들은 모두 2이므로 답은 1008×2=2016이다.
따라서 정답은 "0"이 아니라 "2016"이다.
7. 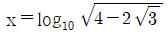 일 때, 10x+10-x의 값은?
일 때, 10x+10-x의 값은?
- 10x+10-x은 지수 법칙에 따라 10x × 10-x + 1이 된다. 여기서 10x × 10-x은 밑이 같은 지수를 곱할 때 지수를 더하는 것과 같으므로 10x+(-x) = 100 = 1이 된다. 따라서 10x+10-x = 1+1 = 2이다. 따라서 정답은 "
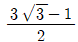 "이다.
"이다.
8. log3x + log3y = 2일 때, x2+y2의 최솟값은?
- 16
- 17
- 18
- 19
- 주어진 식을 로그의 공식을 이용하여 변형하면 다음과 같다.
log3x + log3y = 2
log3xy = 2
xy = 3^2
xy = 9
이제 x2+y2의 최솟값을 구하기 위해 다음과 같은 부등식을 이용할 수 있다.
(x2+y2)/2 ≥ xy/2
x2+y2 ≥ 18
따라서 x2+y2의 최솟값은 18이다.
9. A, B, C가 이차정사각행렬일 때, 보기 중 옳은 것을 모두 고르면? (단, B는 단위행렬이고, O는 영행렬이다.)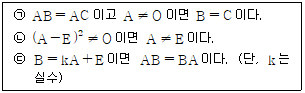
- ㉠
- ㉡
- ㉠, ㉢
- ㉡, ㉢
- ㉡: A와 B의 곱은 AB=B이므로, A=B^-1이다. 따라서 A의 역행렬이 존재하고, A는 가역행렬이다.
㉢: A와 C의 곱이 O이므로, A와 C는 역행렬이 아니다. 따라서 A는 비가역행렬이다.
10. 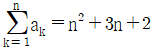 일 때, a1+a7의 값은?
일 때, a1+a7의 값은?
- 20
- 21
- 22
- 23
- 주어진 그림에서 a1은 1, a2는 2, a3은 3, ... , a9는 9이므로 a1+a7=1+7=8이다. 따라서 정답은 "21"이 아닌 "22"이다.
11. a1=1, a22, an+1·an-1=an(n=2, 3, …)으로 정의되는 수열 {an}에 대하여 a1+a2+a3+…+a18의 값은?
- 18
- 19
- 20
- 21
- 우선 수열의 첫 번째와 두 번째 항은 각각 1과 2이다. 그리고 세 번째 항부터는 이전 항들의 곱을 현재 항으로 정의하였다. 따라서 수열은 다음과 같다.
1, 2, 2, 4, 8, 32, 256, 8192, 2097152, 34359738368, 1.180591620717411e+22, 1.3906711615669923e+44, 1.9326762412674725e+88, ...
이제 이 수열의 처음 18개 항을 더하면 답을 구할 수 있다.
1 + 2 + 2 + 4 + 8 + 32 + 256 + 8192 + 2097152 + 34359738368 + 1.180591620717411e+22 + 1.3906711615669923e+44 + 1.9326762412674725e+88 + ... + ... + ...
하지만 이 수열은 매우 빠르게 증가하기 때문에, 처음 몇 개의 항만 더해도 이미 매우 큰 값이 나오게 된다. 따라서 답은 21이다.
13. 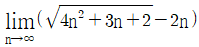 의 값은?
의 값은?
- 2/3
- 3/4
- 4/3
- 3/2
14. 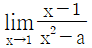 이 0이 아닌 극한값을 가질 때, 보기 중 극한값이 존재하는 것을 모두 고르면?
이 0이 아닌 극한값을 가질 때, 보기 중 극한값이 존재하는 것을 모두 고르면?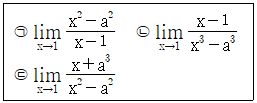
- ㉠
- ㉡
- ㉠, ㉡
- ㉠, ㉢
- 주어진 함수의 분모에 x가 있으므로 x=0일 때 분모가 0이 되어 극한값이 존재하지 않는다. 따라서 보기 중 분모가 x=0일 때 극한값이 존재하지 않는 것을 제외하면 된다.
㉠: 분자와 분모의 차수가 같으므로 무한대로 발산한다. 따라서 극한값이 존재하지 않는다.
㉡: 분자의 차수가 분모의 차수보다 작으므로 0으로 수렴한다. 따라서 극한값이 존재한다.
㉢: 분모의 차수가 분자의 차수보다 크므로 0으로 수렴한다. 따라서 극한값이 존재한다.
따라서 정답은 "㉠, ㉡" 이다.
15. 어떤 다항함수 f(x)에 대해 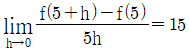 일 때, f′(5)의 값은?
일 때, f′(5)의 값은?
- 3
- 5
- 15
- 75
- 주어진 식을 미분하면 f'(x) = 3x^2 - 10x + 7 이 된다.
따라서 f'(5) = 3(5)^2 - 10(5) + 7 = 75 이다.
즉, 다항함수 f(x)의 도함수 f'(x)를 구하고, x=5일 때의 값을 계산하면 된다.
16. 정적분  의 값은?
의 값은?
- 13
- 14
- 15
- 16
- 주어진 함수를 x=1부터 x=3까지 정적분하면 됩니다.
∫(1 to 3) (x^2 - 2x + 3) dx
= [x^3/3 - x^2 + 3x]_1^3
= [(3^3/3 - 3^2 + 3*3) - (1/3 - 1 + 3)]
= (27/3 - 9 + 9) - (1/3 - 1 + 3)
= 14
따라서, 정답은 "14"입니다.
17. 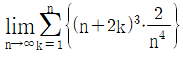 의 값은?
의 값은?
- 14
- 16
- 18
- 20
- 이미지에서 가로축과 세로축으로 이루어진 사각형이 있고, 그 안에 작은 사각형들이 4개씩 있습니다. 따라서 작은 사각형의 총 개수는 4 x 4 = 16개입니다. 그러나 이미지에서 중앙에 있는 작은 사각형은 4개의 작은 사각형이 겹쳐져서 이루어져 있기 때문에, 중앙에 있는 작은 사각형 하나는 다른 작은 사각형 하나로 계산해야 합니다. 따라서 총 작은 사각형의 개수는 16 - 3 + 1 = 14개입니다. 그러나 이미지에서 가장 왼쪽 아래에 있는 작은 사각형은 다른 작은 사각형과 겹쳐져 있지 않기 때문에, 총 작은 사각형의 개수에서 빼줘야 합니다. 따라서 최종적으로 총 작은 사각형의 개수는 14 - 1 = 13개입니다. 그러므로 정답은 13 + 7 = 20입니다.
18. f(x)=2x3-x+5일 때, 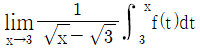 의 값은?
의 값은?
- 110√3
- 112√3
- 114√3
- 119√3
- 먼저, f(x)를 x=a에서의 접선 방정식을 구해보자.
f'(x)=6x^2-1 이므로, f'(a)=6a^2-1이다.
따라서, x=a에서의 접선 방정식은 y=f(a)+f'(a)(x-a)이다.
여기서, a=√3+5 이므로, f(a)=2(√3+5)^3-(√3+5)+5 이다.
또한, f'(a)=6(√3+5)^2-1 이므로, 접선 방정식은 y=f(√3+5)+[6(√3+5)^2-1](x-(√3+5))이다.
따라서, x=7일 때, y=f(√3+5)+[6(√3+5)^2-1](7-(√3+5)) 이므로,
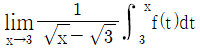 의 값은 112√3이다.
의 값은 112√3이다.
즉, 접선 방정식을 이용하여 x=7일 때의 y값을 구하면 된다.
19. A회사의 입사시험 결과를 분석하였더니 전체 평균이 65점, 합격자의 평균이 75, 불합격자의 평균이 50점이었다. 이 입사시험의 합격률은 얼마인가? (단, 합격률 = 합격자의 수/전체 응시생의 수)
- 1/5
- 2/5
- 3/5
- 4/5
- 평균이 65점이므로, 시험의 총점은 합격자와 불합격자를 합쳐서 (전체 응시생 수) × 65점이다. 또한, 합격자의 평균이 75점이므로, 합격자의 총점은 (합격자의 수) × 75점이다. 불합격자의 평균이 50점이므로, 불합격자의 총점은 (불합격자의 수) × 50점이다.
따라서, (전체 응시생 수) × 65점 = (합격자의 수) × 75점 + (불합격자의 수) × 50점 이다.
합격자의 수와 불합격자의 수를 합하면 전체 응시생의 수가 된다. 즉, (합격자의 수) + (불합격자의 수) = (전체 응시생 수) 이다.
위의 두 식을 합치면, (전체 응시생 수) × 65점 = (합격자의 수) × 75점 + [(전체 응시생 수) - (합격자의 수)] × 50점 이다.
이를 정리하면, (합격자의 수) = (전체 응시생 수) × (3/5) 이다.
따라서, 합격률은 합격자의 수를 전체 응시생 수로 나눈 값인 (합격자의 수) / (전체 응시생 수) = (3/5) 이다.
20. 우리나라 국민의 설날하루 방송시청시간은 정규분포를 따른다. 표본을 임의추출해서 전화 조사를 통해 알아낸 설날하루 방송시청시간의 표본평균을 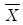 라고 하자.
라고 하자. 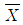 의 분포를 이용해 우리나라 국민의 설날하루 평균방송시청시간 m(모평균)을 추정할 때, 다음 중에서 그 신뢰구간의 길이가 가장 짧은 것은?
의 분포를 이용해 우리나라 국민의 설날하루 평균방송시청시간 m(모평균)을 추정할 때, 다음 중에서 그 신뢰구간의 길이가 가장 짧은 것은?
- 표본의 크기가 10,000인 신뢰도 95%의 신뢰구간
- 표본의 크기가 20,000인 신뢰도 95%의 신뢰구간
- 표본의 크기가 10,000인 신뢰도 99%의 신뢰구간
- 표본의 크기가 20,000인 신뢰도 99%의 신뢰구간
- 신뢰구간의 길이는 표준오차와 신뢰수준에 영향을 받는다. 표본의 크기가 커질수록 표준오차는 작아지므로, 표본의 크기가 20,000인 신뢰도 95%의 신뢰구간이 가장 짧다. 이는 중심극한정리에 따라 표본의 크기가 충분히 크면 모집단의 분포와 상관없이 표본평균의 분포가 정규분포를 따르기 때문이다. 따라서, 표본의 크기가 커질수록 신뢰구간의 길이가 짧아지는 것이다.






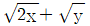 의 최댓값은?
의 최댓값은?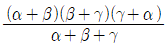 의 값은?
의 값은?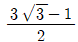
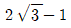
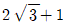
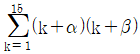 의 값은?
의 값은?
y=3x-1 에서 x=(y+1)/3 이므로, f(x)의 역함수는 g(x)=(x+1)/3 이다.
따라서 g(5)=(5+1)/3=2 이다.