1과목: 수학
1. 두 집합 A={1, 2, 3, 4, 5}, B={4, 5, 6, 7, 8}에 대하여 X-B=ø, (B-A)∪X=X를 만족하는 집합 X의 개수는?
- 4
- 6
- 8
- 16
2. 실수 전체의 집합 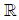 의 임의의 두 원소 a, b에 대하여 연산 ⊕를 a⊕b=a+b-2로 정의할 때, 연산 ⊕에 대한 3의 역원은?
의 임의의 두 원소 a, b에 대하여 연산 ⊕를 a⊕b=a+b-2로 정의할 때, 연산 ⊕에 대한 3의 역원은?
- 1
- 2
- 3
- 4
3. x의 다항식 P(x)에 대하여 (x8-1)P(x)=x11+ax3+b가 모든 실수 x에 대하여 성립할 때, a-b의 값은? (단, a, b는 상수이다.)
- -3
- -2
- -1
- 0
4. 삼차방정식 x3-4x2+3x+1=0의 세 근을 a, b, c라고 할 때, a3+b3+c3의 값은?
- 21
- 25
- 29
- 33
5. 방정식 x3-1=0의 한 허근을 ω라 할 때, ω92+ω16+3의 값은?
- 0
- 1
- 2
- 3
6. 원 x2+y2=1을 x축, y축의 방향으로 각각 –1, -2만큼 평행이동시킨 후, 다시 x축에 대하여 대칭이동시킨 원의 중심의 좌표를 (a ,b)라 할 때, b-a의 값은?
- 0
- 1
- 2
- 3
7. 세 함수 f(x)=2x, g(x)=x+1, h(x)=x2-3에 대하여 (f∘(g∘h))(x)는?
- 2x2-2
- 2x2-4
- 4x2-2
- 4x2-4
8. x에 대한 이차방정식 2x2-x+k=0의 두 근이 sinθ, cosθ일 때, 상수 k의 값은?
9. 이차 정사각행렬 A, B와 이차 단위행렬 E에 대하여 A+B=2E, AB=O일 때, A2+B2를 구하면?
- 4E
- 6E
- 8E
- 10E
10. log2=0.3010, log3=0.4771을 이용하여 61000이 몇 자리 정수인지 구하면?
- 777
- 778
- 779
- 780
11. 자연수 n에 대하여 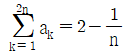 일 때, a21+a22의 값은?
일 때, a21+a22의 값은?
- 1/107
- 1/108
- 1/109
- 1/110
12. 극한  의 값은? (단, θ는 상수이다.)
의 값은? (단, θ는 상수이다.)
- 1
- 1 + cosθ
- 1 + tanθ
- 1 + sinθ
13. 수열 {an}이 a1=, 2nan+1=(n+1)an(n=1, 2, 3, …)을 만족시킬 때, a11의 값은?
- 11/2048
- 11/1024
- 11/512
- 11/256
14. 실수 전체의 집합에서 연속인 함수 f(x)에 대하여 (x+1)f(x)=x2+3x+a가 성립할 때, f(1)의 값은? (단, a는 상수이다.)
- 1
- 2
- 3
- 4
15. 곡선 y=2x3-x-1 위의 점 (1, 0)에서 접선의 방정식이 y=ax+b일 때, a-b의 값은? (단, a, b는 상수이다.)
- 7
- 8
- 9
- 10
16. 다항함수 f(x)가  를만족시킬 때, f(1)의 값은?
를만족시킬 때, f(1)의 값은?
- 1
- 2
- 3
- 4
17. 곡선 y=x3-4x와 x축으로 둘러싸인 부분의 넓이는?
- 2
- 4
- 6
- 8
18. 원점을 출발하여 수직선 위를 움직이는 점 P의 t초 후의 속도 v(t)가 v(t)=8-t3이다. 점 P가 원점을 출발하여 다시 원점을 지날 때까지 움직인 거리는?
- 24
- 25
- 26
- 27
19. 자연수 n에 대하여 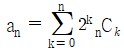 일 때,
일 때, 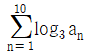 의 값은?
의 값은?
- 54
- 55
- 56
- 57
20. 0≦x≦1에서 정의된 확률 변수 X에 대하여, 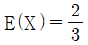 ,
,  이다. E(X2)의 값은?
이다. E(X2)의 값은?
- 1
- 1/2
- 1/3
- 1/4








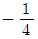

B-A={6,7,8} 이므로 X는 {4,5,6,7,8}의 부분집합이어야 한다. 이 중에서 B의 부분집합이면서 (B-A)의 부분집합인 집합은 {4,5}, {4,5,6}, {4,5,7}, {4,5,6,7} 이렇게 4개가 있다. 따라서 정답은 "4"이다.