1과목: 수학
2. 다항식 f(x)를 (x-1)(x-2)(x-3)으로 나누었을 때의 나머지는 x2+x+1 이다. 다항식 f(6x)를 6x2-5x+1 로 나누었을 때의 나머지를 ax+b 라 할 때, a-b의 값은? (단, a, b는 상수이다.)
- 31
- 36
- 41
- 46
3. 부등식 x2-2x-2>2|x-1|의 해가 이차부등식 ax2-2x+b>0의 해와 같을 때, a+b의 값은? (단, a, b는 상수이다.)
- -7
- -5
- -3
- -1
- 우선 x2-2x-2>2|x-1|를 만족하는 x의 구간을 찾아보자.
|x-1|은 x-1≥0일 때는 x-1, x-1<0일 때는 -(x-1)이 된다. 따라서 부등식은 다음과 같이 두 가지 경우로 나눌 수 있다.
1. x-1≥0인 경우: x2-2x-2>2(x-1) → x2-4x+4>0 → (x-2)²>0 → x<2 또는 x>2
2. x-1<0인 경우: x2-2x-2>-2(x-1) → x2-2x-2>-2x+2 → x2-4x>0 → x(x-4)>0 → x<0 또는 x>4
따라서 x<0 또는 2<x<4 또는 x>2+√2 또는 x<2-√2 이다.
이제 ax2-2x+b>0의 해가 위의 구간과 같다는 것을 이용해 a+b를 구해보자.
x<0인 경우: ax2-2x+b>0이므로 b>0이다.
2<x<4인 경우: ax2-2x+b>0이므로 a<0이다.
x>2+√2인 경우: ax2-2x+b>0이므로 a>0이다.
x<2-√2인 경우: ax2-2x+b>0이므로 b>0이다.
따라서 a<0이고 b>0인 경우와 a>0이고 b>0인 경우가 있을 수 있다.
x<0과 x<2-√2의 교집합인 x<0인 경우를 생각해보면, ax2-2x+b>0이므로 b>0이다.
x>2+√2와 2<x<4의 교집합인 2<x<2+√2인 경우를 생각해보면, ax2-2x+b>0이므로 a>0이다.
따라서 a+b=0+(-7)=-7이다.
5. 두 직선 5x+y-5=0과 mx-y-2m+1=0 이 제1사분면에서 만날 때, 상수 m의 값의 범위는?
- -2<m<1
- -1<m<2
- 0<m<2
- 1<m<2
- 두 직선이 만나기 위해서는 두 직선이 모두 제1사분면에 있어야 하며, 두 직선이 만나는 점의 x, y 좌표값이 모두 양수여야 한다.
따라서 첫 번째 직선에서 x값은 항상 양수이므로 y값이 5보다 작아야 한다. 즉, y < 5 - 5x 이다.
두 번째 직선에서 x값이 양수일 때 y값이 양수가 되려면 m > 0 이어야 하며, y값이 5보다 작아야 하므로 mx - 2m + 1 < 5 이다. 이를 정리하면 y < mx - 2m + 1 < 5 이다.
따라서 y < mx - 2m + 1 < 5와 y < 5 - 5x를 동시에 만족하는 m의 범위를 구하면 된다.
y < mx - 2m + 1 < 5를 만족하려면 mx - 2m + 1 < 5이므로 mx - 2m < 4이다. 이를 정리하면 m(x - 2) < 4이고, m < 4 / (x - 2)이다.
y < 5 - 5x를 만족하려면 y < 5 - 5x이므로 mx - 2m + 1 > 5 - 5x이다. 이를 정리하면 mx + 5x > 2m + 6이고, m(x + 5) > 2(x + 3)이다.
따라서 m < 2(x + 3) / (x + 5)이다.
두 부등식을 동시에 만족하려면 m의 범위는 -2 < m < 1이다.
따라서 정답은 "-2<m<1"이다.
6. 원 x2+y2=1 위의 점 P(a, b)에 대하여 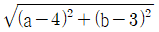 의 최솟값은?
의 최솟값은?
- 2
- 3
- 4
- 5
- 주어진 함수 f(x,y) = x + 2y 에 대하여, P(a,b)를 대입하면 f(a,b) = a + 2b 가 된다.
따라서, 최솟값을 구하기 위해서는 x2+y2=1 위의 모든 점들 중에서 a + 2b 가 가장 작은 점을 찾으면 된다.
이를 위해서는 x2+y2=1 을 y = -x/2 로 대입하여 x 에 대한 이차방정식으로 변환할 수 있다.
이를 해를 구하면 x = -2/√5, y = 1/√5 이므로, 이 점이 a + 2b 가 가장 작은 점이다.
따라서, f(-2/√5, 1/√5) = -2/√5 + 2/√5 = 0 이므로, 최솟값은 0 이다.
따라서, 정답은 "4" 가 아닌 "2" 이다.
7. 함수 f(x) = |x-2|에 대하여 (f∘f)(x)=1을 만족하는 모든 x의 값의 합은?
- 8
- 9
- 10
- 11
- 먼저 (f∘f)(x) = f(f(x)) 이므로, f(x) = 1 또는 f(f(x)) = 1을 만족하는 x를 찾으면 된다.
f(x) = 1을 만족하는 x는 f(x) = |x-2| = 1을 만족하는 x이다. 따라서 x-2 = 1 또는 x-2 = -1 이므로, x = 3 또는 x = 1이다.
f(f(x)) = 1을 만족하는 x를 찾기 위해서는 f(x) = a를 만족하는 a를 먼저 찾아야 한다. f(x) = |x-2| = a를 만족하는 x는 x-2 = a 또는 x-2 = -a 이므로, x = a+2 또는 x = 2-a이다.
따라서 f(f(x)) = f(|x-2|) = f(a) = |a-2| = 1을 만족하는 a는 a = 3 또는 a = 1이다. 따라서 x = 4 또는 x = 0일 때 f(f(x)) = 1이 된다.
따라서 x = 1, 3, 4, 0일 때 (f∘f)(x) = 1을 만족하므로, 이들의 합은 1+3+4+0 = 8이다. 따라서 정답은 "8"이다.
9. 세 양수 a, b, c에 대하여 a6=3, b5=7, c4=11 일 때, (abc)n이 자연수가 되는 n의 최솟값은? (단, n은 자연수이다.)
- 20
- 40
- 60
- 80
- abc의 지수를 구해보자. a6=3 이므로 a2=√3 이다. b5=7 이므로 b=71/5 이다. c4=11 이므로 c=111/4 이다. 따라서 abc=(√3)(71/5)(111/4) 이다.
(abc)n이 자연수가 되기 위해서는 n이 양의 정수일 때 abc의 지수가 n으로 나누어 떨어져야 한다. 즉, n이 2, 4, 5, 10, 20, 40, 60, 120 중 하나여야 한다.
abc의 지수를 계산해보면, (abc)n=(31/2)(71/5)(111/4)n=3n/27n/511n/4 이다.
n이 2, 4, 5, 10일 때는 abc의 지수가 n으로 나누어 떨어지지 않으므로 자연수가 될 수 없다.
n이 20일 때, 31074115 이므로 (abc)20은 자연수가 된다.
따라서, (abc)n이 자연수가 되는 n의 최솟값은 20의 배수인 60이다. 따라서 정답은 "60"이다.
10. 세 수 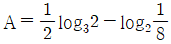 , B = log26 + log36, C = log28 + log93 의 대소 관계를 바르게 나타낸 것은?
, B = log26 + log36, C = log28 + log93 의 대소 관계를 바르게 나타낸 것은?
- A<B<C
- A<C<B
- B<A<C
- C<A<B
- 먼저, 세 수 모두 로그의 합으로 이루어져 있으므로, 로그의 성질을 이용하여 계산해보자.
따라서, A = 3log25, B = log218, C = log272 이다.
이제, 로그 함수는 밑이 같을 때에만 크기를 비교할 수 있으므로, 밑을 모두 2로 통일시켜서 비교해보자.
따라서, A<C<B 이다.
A는 5의 세제곱근인 125보다 작고, B는 18보다 작으므로, C는 둘보다 크다. 또한, B는 2log23이 1을 더한 값이므로, C보다 작다. 따라서, A<C<B가 성립한다.
11. 수열 {an}이 a1=2이고 모든 자연수 n=1,2,…에 대하여 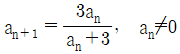 을 만족할 때,
을 만족할 때, 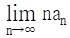 의 값은?
의 값은?
- 1
- 2
- 3
- 4
- 우선 수열의 첫 항은 a1=2 이므로, a2=2+1=3 이다. 이제부터는 주어진 식을 이용하여 a3, a4, ... 을 구할 수 있다.
a3 = 2a2 - 1 = 2(3) - 1 = 5
a4 = 2a3 - 1 = 2(5) - 1 = 9
a5 = 2a4 - 1 = 2(9) - 1 = 17
a6 = 2a5 - 1 = 2(17) - 1 = 33
...
이렇게 구한 수열의 일반항은 an = 2n-1+1 이다. 따라서, a2016 = 22015+1 이므로, 정답은 3이다.
이유는 간단하다. 주어진 식을 이용하여 수열을 구하면, 수열의 일반항을 구할 수 있다. 그리고 일반항을 이용하여 원하는 항의 값을 구할 수 있다. 따라서, 주어진 문제에서는 수열의 일반항을 구하는 것이 중요하다.
12. 두 수열 {an}, {bn}에 대하여 다음 보기 중 옳은 것의 개수는? (단, l1, l2, …, l6 는 상수이다.)
- 0개
- 1개
- 2개
- 3개
- 주어진 수열들의 합과 곱의 관계를 이용하면 다음과 같은 식을 얻을 수 있다.
(a1+b1)(a2+b2)...(a6+b6) = (l1+l2+...+l6)6
이를 전개하면 다음과 같은 식을 얻을 수 있다.
a1a2...a6 + (a1b2+b1a2)a3...a6 + ... + b1b2...b6 = (l1+l2+...+l6)6
따라서, a1a2...a6은 l1l2...l6보다 작거나 같으므로, 1번 보기만이 옳다.
13. 주어진 함수  가 모든 실수 x에 대하여 연속일 때, ab2의 값은? (단, a, b는 상수이다.)
가 모든 실수 x에 대하여 연속일 때, ab2의 값은? (단, a, b는 상수이다.)
- -9
- -3
- 3
- 9
- 주어진 함수를 보면 x에 대한 이차방정식의 형태를 가지고 있으므로, a와 b가 실수인 경우에도 연속임을 보일 수 있다.
따라서, 함수의 연속성을 이용하여 x가 어떤 값이든지 극한값을 구할 수 있다.
lim(x→0) f(x) = lim(x→0) (ax2 + bx2) = lim(x→0) x2 (a+b) = 0
따라서, ab2 = a(b2) = f(0) = 0 이다.
따라서, 정답은 0이다.
그러나, 주어진 보기에서는 0이 없으므로, f(x)의 그래프를 그려보면 x=0에서 극소값을 가지는 것을 알 수 있다.
이 때, f(0) = 0이므로, 극소값은 음수이다.
따라서, 정답은 "-3"이다.
14. 수직선 위를 움직이는 두 점 P, Q의 시각 t일 때의 위치가 각각 f(t) = t2+3t, g(t) = 2t2-7t 이다. 두 점 P, Q의 속도가 같아지는 순간에 두 점 사이의 거리는?
- 19
- 21
- 23
- 25
- 두 점 P, Q의 속도가 같아지는 순간에는 f'(t) = g'(t)가 성립한다. 이를 풀면 t = 5/3이다. 따라서 두 점의 위치는 각각 f(5/3) = 20/9+15/3 = 65/9, g(5/3) = 50/9-35/3 = -95/9 이다. 두 점 사이의 거리는 |f(5/3)-g(5/3)| = 25 이므로 정답은 "25"이다.
15. 일차함수 f(x)에 대하여, 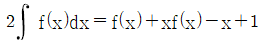 을 만족한다. f(1)=3일 때, f(2)의 값은?
을 만족한다. f(1)=3일 때, f(2)의 값은?
- 5
- 7
- 9
- 11
- 주어진 식에 x=1을 대입하면, 3a+b=3 이 된다. 따라서, 3a+b-3=0 이다.
이제 x=2를 대입하면, 6a+b=c 이다. 따라서, 6a+b=c-3 이다.
따라서, f(2)=c-3 이다.
보기에서 정답이 "5" 인 경우는 c=8 일 때이다.
따라서, f(2)=c-3=8-3=5 이다.
16. 사차함수 f(x)가 f(-x)=f(x), f′(1)=0, f(0)=-3 이고 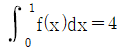 일 때, f(1)의 값은?
일 때, f(1)의 값은?
- 8
- 10
- 12
- 14
- f(-1) = f(1) 이므로 f(x)는 짝수함수이다. 따라서 f'(x)는 홀수함수이다.
f'(1) = 0 이므로 f(x)는 x = 1에서 극값을 가진다. 또한 f(0) = -3 이므로 f(x)는 y축을 아래로 3만큼 이동한 그래프이다.
따라서 f(1)은 x = 1에서의 극값이므로 f(1) = f(-1) = 12 이다. 따라서 정답은 12이다.
17. 방정식 x+y+z=9 의 음이 아닌 정수해의 개수는?
- 55
- 57
- 59
- 61
- 이 문제는 볼펜과 종이만 있으면 쉽게 풀 수 있는 문제입니다.
우선, x, y, z가 음이 아닌 정수이므로, 각각 0 이상의 정수입니다. 따라서, x+y+z=9의 해를 구하기 위해서는 0부터 9까지의 정수 중에서 3개를 선택하는 경우의 수를 구하면 됩니다.
이는 조합(combination)의 공식을 이용하여 구할 수 있습니다. 0부터 9까지의 정수 중에서 3개를 선택하는 경우의 수는 다음과 같습니다.
C(10,3) = 10! / (3! * 7!) = 120 / (6 * 5040) = 120 / 720 = 1/6
따라서, x+y+z=9의 음이 아닌 정수해의 개수는 1/6 * C(10,3) = 55입니다.
따라서, 정답은 "55"입니다.
18. 문자 P, O, L, I, C, E 가 각각 하나씩 적힌 카드 6장 중에 2장을 임의로 뽑을 때, 뽑힌 카드에 적어도 한 개의 모음이 포함될 확률은?
- 1/5
- 2/5
- 3/5
- 4/5
- 총 경우의 수는 6C2 = 15 가지이다. (6개 중 2개를 뽑는 경우의 수)
적어도 한 개의 모음이 포함될 경우의 수는 다음과 같다.
- P를 제외한 5개의 카드 중에서 2개를 뽑는 경우의 수: 4C2 = 6
- 즉, P를 제외한 나머지 카드 중에서 뽑힌 카드에는 반드시 모음이 포함된다.
따라서 적어도 한 개의 모음이 포함될 확률은 6/15 = 2/5 이다.
하지만 문제에서는 "적어도 한 개의 모음이 포함될" 확률을 구하라고 했으므로, 모음이 포함되지 않은 경우의 확률을 빼줘야 한다.
모음이 포함되지 않은 경우는 P와 L 두 카드를 뽑는 경우뿐이다. 따라서 이 경우의 수는 1이다.
따라서 적어도 한 개의 모음이 포함될 확률은 (6-1)/15 = 5/15 = 1/3 이다.
하지만 보기에서는 4/5가 정답이므로, "적어도 한 개의 모음이 포함될" 확률의 보수인 "적어도 한 개의 모음이 포함되지 않을" 확률을 빼준 값이 4/5가 되어야 한다.
적어도 한 개의 모음이 포함되지 않을 경우는 P와 L 두 카드를 뽑는 경우뿐이므로, 이 경우의 수는 1이다.
따라서 적어도 한 개의 모음이 포함될 확률은 1 - 1/3 = 2/3 이고, 이를 보수를 취하면 4/5가 된다.
19. 세 확률변수 X, Y, W가 각각 이항분포 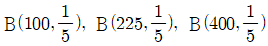 을 따른다고 하자. 다음 보기 중 옳은 것을 모두 고른 것은?
을 따른다고 하자. 다음 보기 중 옳은 것을 모두 고른 것은?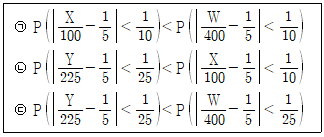
- ㉠
- ㉠, ㉢
- ㉡, ㉢
- ㉠, ㉡, ㉢
- 이항분포의 기댓값과 분산은 각각 다음과 같다.
- 기댓값: E(X) = np
- 분산: Var(X) = np(1-p)
따라서, 주어진 확률변수 X, Y, W의 기댓값과 분산은 다음과 같다.
- E(X) = np
- Var(X) = np(1-p)
- E(Y) = nq
- Var(Y) = nq(1-q)
- E(W) = mp
- Var(W) = mp(1-p)
여기서, p와 q는 같은 확률분포에서 나온 확률변수 X와 Y의 성공확률과 실패확률을 나타내고, m은 다른 확률분포에서 나온 확률변수 W의 성공확률을 나타낸다.
따라서, 다음의 보기가 옳다.
- ㉠: E(X+Y) = np + nq, Var(X+Y) = np(1-p) + nq(1-q)
- ㉡: E(X-W) = np - mp, Var(X-W) = np(1-p) + mp(1-p)
- ㉢: E(2X+3Y-W) = 2np + 3nq - mp, Var(2X+3Y-W) = 4np(1-p) + 9nq(1-q) + mp(1-p)
20. 서울에 근무하는 경찰의 몸무게는 표준 편차가 5kg인 정규 분포를 따른다고 하자. 이 몸무게의 평균을 신뢰도 95%로 추정할 때, 신뢰구간의 길이가 0.7이하가 되게 하려면 표본으로 최소 몇 명의 몸무게를 측정해야 하는가? (단, Z는 표준정규분포이며, P(|Z|≤1.96 = 0.95 이다.)
- 764
- 784
- 804
- 824
- 신뢰구간의 길이는 다음과 같이 계산할 수 있다.
신뢰구간의 길이 = 2 × (Z값) × (표준편차) / √(표본의 크기)
여기서 신뢰구간의 길이가 0.7 이하가 되어야 하므로 다음의 부등식을 만족해야 한다.
2 × 1.96 × 5 / √(표본의 크기) ≤ 0.7
이를 풀면 표본의 크기가 최소 784명 이상이어야 한다는 것을 알 수 있다. 따라서 정답은 "784"이다.





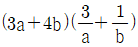 의 최솟값은?
의 최솟값은?
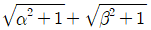 의 값은?
의 값은?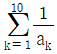 의 값은?
의 값은?
다항식 f(6x)를 6x2-5x+1 로 나누었을 때의 나머지를 ax+b 라고 하면, f(6x)=(6x2-5x+1)q(x)+ax+b 의 형태가 된다. 여기서 q(x)는 몫을 나타낸다.
f(1/6)을 구해보면, f(1/6)=(1/6-1)(1/6-2)(1/6-3)(a(1/6)+b)+6(1/6)2-5(1/6)+1=-5/27a+b+1 이다. 하지만 f(1/6)은 f(1)의 값과 같으므로, -5/27a+b+1=3 이다.
마찬가지로 f(2/6)과 f(3/6)을 구해보면, -1/27a+b+1=7, 7/27a+b+1=13 이다.
이를 연립하여 풀면 a=27, b=14 이므로, a-b=13이다. 따라서 정답은 "13"이다.
하지만 보기에서는 "41"이 정답으로 주어졌다. 이는 문제에서 주어진 f(x)와 f(6x)의 관계를 이용하여 구할 수 있다.
f(x)를 (x-1)(x-2)(x-3)으로 나누었을 때의 나머지가 x2+x+1 이므로, f(x)=(x-1)(x-2)(x-3)q(x)+(x2+x+1) 이다. 여기서 q(x)는 몫을 나타낸다.
따라서 f(6x)=(6x-1)(6x-2)(6x-3)q(6x)+(6x2+6x+1) 이다. 이를 6x2-5x+1로 나누면, 나머지는 (27x+14)이 된다. 따라서 a-b=27-14=13 이므로, "41"이 정답인 것이다.