1과목: 수학
1. 방정식 x2-√7x+1=0 을 만족하는 실수 x에 대하여, 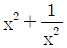 의 값은?
의 값은?
- 5
- 7
- 9
- 11
2. 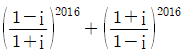 을 간단히 하면? (단, i=√-1)
을 간단히 하면? (단, i=√-1)
- 0
- 1
- 2
- 3
3. 이차함수 y=x2-x+k의 그래프가 x축과 만나는 두 점 사이의 거리가 √5일 때, 상수 k의 값은?
- -7
- -5
- -3
- -1
4. -1≤x≤1 일 때, y=(x2-2x+1)2-2(x2-2x+1)+2의 최댓값 α와 최솟값 β의 차 α-β를 구하면?
- 8
- 9
- 10
- 11
5. 이차부등식 –x2-2(m-1)x+(m-3)>0을 만족하는 실수 x가 존재하지 않을 때, 실수 m의 값의 범위는?
- -2≤m≤1
- -1≤m≤2
- 0≤m≤2
- 2≤m≤3
6. 방정식 5x2+y2-4xy+2x+1=0을 만족하는 실수 x, y에 대하여, x+y의 값은?
- -1
- 2
- -3
- 4
7. logx의 지표가 2일 때, logx의 가수와 log√x의 가수가 같도록 하는 실수 x의 값은?
- √10
- 10
- 10√10
- 100
8. 수열 {an}의 첫째 항부터 제n항까지의 합 Sn이 Sn=3n+1+k 일 때, 수열 {an}이 첫째 항부터 등비수열을 이루기 위한 상수 k의 값은?
- -3
- -2
- -1
- 0
9. 원 x2+y2-2x+2y-6=0 위의 점에서 직선 y=x-8에 이르는 거리의 최솟값은?
- 1
- √2
- 3
- 2√2
10. 부등식 2[x]2-5[x]+2<0의 해가 α≤x≤β일 때, α+β의 값은? (단, [x]는 x보다 크지 않은 최대의 정수이다.)
- 3
- 4
- 5
- 6
11. n≥3인 자연수 n에 대하여, 곡선 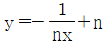 과 직선 y=(n-2)x가 만나는 두 교점의 x좌표를 An, Bn이라 할 때, 급수
과 직선 y=(n-2)x가 만나는 두 교점의 x좌표를 An, Bn이라 할 때, 급수 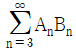 을 구하면?
을 구하면?
12. 실수 전체에서 정의된 함수 y=f(x)는 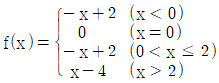 라 정의되고, 다항식 g(x)는
라 정의되고, 다항식 g(x)는 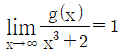 , g(0)=2, 그리고 합성함수 (g∘f)(x)는 실수 전체에서 연속임을 만족한다 하자. 이때 g(1)를 구하면?
, g(0)=2, 그리고 합성함수 (g∘f)(x)는 실수 전체에서 연속임을 만족한다 하자. 이때 g(1)를 구하면?
- -3
- -1
- 1
- 3
13. 미분가능인 두 함수 f(x), g(x)는 아래의 조건을 만족한다 하자. 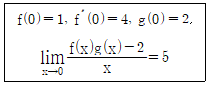
이때 g′(0)을 구하면?
- -3
- -1
- 0
- 2
14. 두 함수 f(x)=x3+3x2+x, g(x)=3x3-11x에 대하여, g(x)를 y축의 방향으로 α만큼 평행이동 시켜 f(x)와 서로 다른 두 점에서만 만나도록 하는 모든 α의 합은?
- -15
- -13
- -5
- 0
15. 함수 f(x)는 모든 실수 x에 대하여, 아래의 세 가지 조건을 만족한다 하자. 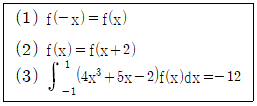
이때 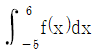 를 구하면?
를 구하면?
- 6
- 15
- 27
- 33
16. 함수 f(x)=x3+2x-2의 역함수를 g(x)라 할 때,  를 구하면?
를 구하면?
- 17/4
- 19/4
- 39/4
- 57/4
17. 집합 A={1, 2, 3, 4, 5}, B={1, 2, 3}이라 하고, 집합 F는 A에서 B로의 함수 중 치역과 공역이 같은 함수들을 다 모아둔 집합이라 하자. F에서 하나의 원소 f를 선택할 때 조건 ‘x1<x2 라면 f(x1)≤f(x2)’를 만족할 확률은?
- 1/25
- 3/25
- 6/25
- 9/25
18. 한 변의 길이가 1인 25개의 정사각형들로 이루어진 아래의 그림과 같은 판 위에서 다음의 규칙으로 주사위 게임을 한다 하자. 
이때 주사위를 5번 던졌을 때 O로부터 길이가 5보다 작은 점에 도착할 확률은?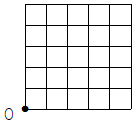
- 30/243
- 120/243
- 210/243
- 1
19. 5개의 자료 x1, x2, …, x5에 대하여 zi=2xi-10(i=1, 2, …, 5)은 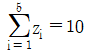 ,
, 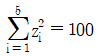 일 때, 자료 x1, x2, …, x5의 분산을 구하면?
일 때, 자료 x1, x2, …, x5의 분산을 구하면?
- 1
- 2
- 3
- 4
20. 크기와 모양이 같은 빨간색 공 3개와 파란색 공 2개가 있는 주머니에서 한 개의 공을 임의로 꺼내어 그 색깔을 확인한 후 다시 주머니 속에 집어 넣는다. 매회 시행마다 빨간색 공을 뽑으면 3점을 획득하고, 파란색 공을 뽑으면 2점을 잃는 게임을 한다 하자. 처음 0점에서 시작하여 이 게임을 150회 시행 후 점수가 180점 이상일 확률을 아래쪽 표준정규분포표를 이용하여 구하면?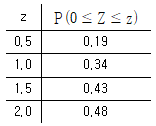
- 0.07
- 0.16
- 0.43
- 0.69






이유: 주어진 식을 계산하면 1+i를 제곱한 값이 나온다.
(1+i)² = 1² + 2i + i² = 1 + 2i - 1 = 2i
따라서, 주어진 식은 2i를 3번 곱한 값이므로, i³ = -i 이다.
그러므로, 주어진 식은 2*(-i) = -2i 이므로, 실수부는 0이고 허수부는 -2인 복소수이다.
따라서, 정답은 2이다.