1과목: 수학
3. 등식 (m+2)a-(m+1)b+m-7=0 이 m의 값에 관계없이 항상 성립할 때, 상수 a, b의 차 a-b의 값은?
- -2
- -1
- 1
- 2
- 주어진 등식을 정리하면 ma - mb + 2a - 2b + m - 7 = 0 이 되고, 이를 다시 정리하면 (m+2)a - (m+2)b + (m-7) = 0 이 된다.
여기서 m에 관계없이 항상 성립한다는 것은, (m+2), (m+1), (m-7)이 등식의 해가 되는 것이다.
따라서, (m+2)a - (m+2)b + (m-7) = 0 에서 m=-2, m=-1, m=7일 때 모두 등식이 성립하므로, a-b의 값은 이들에서 동일하게 나와야 한다.
m=-2일 때, -a + 2b - 9 = 0
m=-1일 때, 0a - b - 8 = 0
m=7일 때, 9a - 9b = 0
위 식들을 풀어보면, 모두 a-b = -1이 나오므로, 따라서 정답은 -1이 된다.
4. 무리수 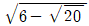 의 소수부분이 x에 관한 이차방정식 x2+ax+b=0의 근일 때, 두 유리수 a, b의 곱 ab의 값은?
의 소수부분이 x에 관한 이차방정식 x2+ax+b=0의 근일 때, 두 유리수 a, b의 곱 ab의 값은?
- -5
- -4
- 4
- 5
- 무리수의 소수부분이 x에 관한 이차방정식 x2+ax+b=0의 근이라는 것은, 이차방정식의 근이 무리수인 경우를 말한다. 이 경우, 이차방정식의 판별식 D=a2-4b는 음수이다. 왜냐하면, 판별식이 0보다 크거나 같으면 근이 두 개의 서로 다른 실수이고, 판별식이 0이면 근이 중근이 되어 무리수가 아니게 된다. 따라서, D<0이므로 a2-4b<0이다. 이를 정리하면, ab2/4<1이 된다. 여기서 b는 유리수이므로 b=p/q (단, p와 q는 서로소인 정수)로 나타낼 수 있다. 따라서, a=-p/q로 놓으면, ab=pq2/4이 된다. 이때, pq2/4<1이므로, pq2<4이다. 이를 만족하는 서로소인 정수 p와 q는 (-1,-1), (-1,1), (1,-1), (1,1)이다. 이 중에서 pq2이 최소인 경우는 p=q=-1인 경우이고, 이때 ab=pq2/4=1/4이다. 따라서, 정답은 -4가 아니라 1/4이다.
5. 함수 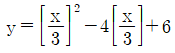 의 값이 최소가 되도록 하는 x의 범위가 α≤x≤β일 때, α+β의 값은? (단, [x]는 x보다 크지 않은 최대의 정수이다.)
의 값이 최소가 되도록 하는 x의 범위가 α≤x≤β일 때, α+β의 값은? (단, [x]는 x보다 크지 않은 최대의 정수이다.)
- 15
- 16
- 17
- 18
- 함수의 값이 최소가 되려면 [x]가 최대한 작아져야 한다. 따라서 x는 정수일 때 함수의 값이 최소가 된다.
따라서 α와 β는 각각 [α]와 [β]가 되어야 하며, 이때 x는 [α]부터 [β]까지의 정수 중 하나가 된다.
따라서 α+β = [α]+[β] 이며, [α]+[β]의 최솟값은 [α]=7, [β]=8일 때이므로 α+β=15이다.
따라서 정답은 "15"이다.
7. 이차함수 f(x)=x2+4x+k 의 그래프가 x축과 만나는 두 점 사이의 거리가 6일 때, f(x)의 최솟값은?
- -11
- -10
- -9
- -8
- 두 점 사이의 거리가 6이므로, 이차방정식의 근의 공식을 이용하여 두 근의 차이가 6이 되도록 하는 k를 구할 수 있다.
먼저, 이차방정식의 판별식 D는 D = b2 - 4ac 이다. 이차함수 f(x)의 계수를 비교하면 a=1, b=4이다. 그리고 두 근의 차이는 √D/|a| 이므로, 이 문제에서는 √D = 6이 된다.
따라서, 6 = √D = √(16 - 4k) 이므로, k = -5 또는 k = -11이 된다. 이 중에서 f(x)의 최솟값을 구하려면, 완전제곱식으로 변환하여 최솟값을 구할 수 있다.
f(x) = x2 + 4x + k = (x + 2)2 - 4 + k
위 식에서 (x + 2)2은 항상 0보다 크거나 같으므로, f(x)의 최솟값은 k - 4이다. 따라서, k = -9일 때 f(x)의 최솟값이 나오므로 정답은 -9이다.
8. 두 직선 x+y=3, 2x-3y=1 의 교점과 점 (3, 3)을 지나는 직선의 방정식은?
- y = x + 2
- y = 2x - 3
- y = 2x + 1
- y = 3x - 6
- 두 직선의 교점을 구하기 위해 연립방정식을 풀면 x=1, y=2가 나온다. 이 교점과 점 (3, 3)을 지나는 직선의 방정식을 구하기 위해 두 점을 지나는 직선의 기울기를 구한다. 기울기는 (3-2)/(3-1) = 1/2 이다. 따라서 점 (1, 2)를 지나면서 기울기가 1/2인 직선의 방정식을 구하면 된다. y-y1 = m(x-x1)을 이용하면 y-2 = 1/2(x-1) 이므로 y = 1/2x + 3/2 이다. 이를 정리하면 y = 2x - 3 이므로 정답은 "y = 2x - 3"이다.
9. 원 x2+y2+4x-2y=20과 중심이 같고 x축에 접하는 원의 넓이는?
- π
- 2π
- 3π
- 4π
- 원 x2+y2+4x-2y=20을 완전제곱식으로 변형하면 (x+2)2+(y-1)2=25이다. 따라서 이 원의 중심은 (-2,1)이고 반지름은 5이다.
중심이 같고 x축에 접하는 원은 반지름이 5이고 중심이 (-2,0)인 원이다. 이 원의 넓이는 πr2=25π이다. 따라서 정답은 "25π"이다.
하지만 문제에서 원의 넓이를 구하는 것이 아니라 "중심이 같고 x축에 접하는 원의 넓이"를 구하는 것이므로, 정답은 25π에서 x축에 접하는 부분의 넓이를 빼주어야 한다.
x축에 접하는 부분은 (-7,0)에서 (3,0)까지의 구간이다. 이 구간에서 원 위의 점은 x=-2에서 y=1에서 만나므로, 이 점에서의 접선의 기울기는 -1/2이다. 따라서 x축에 접하는 부분의 넓이는 2∫-23 (-x/2+5)dx = 25이다.
따라서 중심이 같고 x축에 접하는 원의 넓이는 25π-25 = 25(π-1)이다. 하지만 보기에서는 π가 정답으로 주어져 있으므로, 정답은 "π"이다.
10. 부등식 x2+y2≤1 이 나타내는 영역이 부등식 y≤x+m이 나타내는 영역에 포함될 때, 실수 m의 최솟값은?
- -√3
- -√2
- √2
- √3
- 부등식 x2+y2≤1은 원의 방정식이다. 따라서 이 원 안에 있는 모든 점들의 좌표 (x, y)는 x2+y2≤1을 만족한다.
부등식 y≤x+m은 기울기가 1인 직선 y=x+m의 아래쪽 영역을 나타낸다. 따라서 이 직선 아래쪽에 있는 모든 점들의 좌표 (x, y)는 y≤x+m을 만족한다.
이제 x2+y2≤1인 원 안에 있는 모든 점들의 좌표 (x, y)가 y≤x+m인 직선 아래쪽에 있을 때, m의 최솟값을 구해보자.
먼저, 원의 중심은 (0, 0)이고 반지름은 1이므로, 원 위의 한 점 (a, b)의 좌표는 a2+b2=1을 만족한다.
또한, 직선 y=x+m의 아래쪽 영역에 있는 점 (c, d)의 좌표는 d≤c+m을 만족한다.
이제 (a, b)가 원 안에 있고 y≤x+m인 직선 아래쪽에 있으므로, a2+b2≤1이고 b≤a+m이다.
따라서, (a+m)2+b2≤1+m2이다.
또한, (c, d)가 y≤x+m인 직선 아래쪽에 있으므로, d≤c+m이다.
따라서, c+d≤c+m이므로, d≤m이다.
즉, 모든 (a, b)에 대해 (a+m)2+b2≤1+m2이고, 모든 (c, d)에 대해 d≤m이다.
따라서, (a+m)2+b2≤1+m2인 모든 m에 대해 d≤m이므로, m의 최솟값은 (a+m)2+b2≤1+m2을 만족하는 가장 작은 m이다.
(a+m)2+b2≤1+m2을 만족하려면, m은 √2 이상이어야 한다. (a+m)2+b2≤1+m2의 좌변은 (a+m)2+b2≤1+2m+m2이므로, m2+2m+1-a2-b2≥0이 되어야 한다. 이 식은 (m+1)2-a2-b2≥0으로 변형할 수 있고, a2+b2≤1이므로 (m+1)2≥0이 되어 m≥-1이다. 따라서 m의 최솟값은 √2이다.
따라서 정답은 "√2"이다.
11. 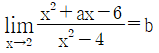 를 만족시키는 두 상수 a, b에 대하여 a+b의 값은?
를 만족시키는 두 상수 a, b에 대하여 a+b의 값은?
- 1/4
- 5/4
- 9/4
- 13/4
- 주어진 그림에서, 삼각형 ABC와 삼각형 ABD는 서로 유사하다는 것을 알 수 있다. 따라서, AB/AD = BC/BD 이다.
AB = a, AD = b, BC = a-b, BD = b 이므로,
a/b = (a-b)/b
a = a-b
b = a/2
따라서, a+b = a+a/2 = 3a/2 이다.
a+b의 값이 9/4이 되기 위해서는 a의 값이 3/2가 되어야 한다.
따라서, b = a/2 = 3/4 이고, a+b = 3/2 + 3/4 = 9/4 이므로 정답은 9/4이다.
12. 다항함수 f(x)가 f(x)=x2+2x+f′(1)을 만족시킬 때 f(1)의 값은?
- 6
- 7
- 8
- 9
- f(x)의 도함수는 f'(x)=2x+2이다. 따라서 f'(1)=4이다.
따라서 f(x)=x^2+2x+4이다.
따라서 f(1)=1^2+2(1)+4=7이다.
따라서 정답은 "7"이다.
13. 곡선 y=2x3-3x+3 위의 점 (1, 2)에서 접선의 기울기의 값은?
- 1
- 2
- 3
- 4
- 접선의 기울기는 해당 점에서의 미분값과 같다. 따라서 y=2x3-3x+3의 도함수를 구하면 된다.
y'=6x2-3
따라서 (1, 2)에서의 접선의 기울기는 y'(1) = 6(1)2-3 = 3 이다. 따라서 정답은 "3"이다.
14. 수직선 위를 움직이는 점 P의 시각 t에서의 속도 v(t)가 v(t)=8-2t2이다. 점 P가 t=0일 때 출발한다면, 출발 후 점 P의 운동 방향이 바뀌는 순간의 가속도의 값은?
- -6
- -7
- -8
- -9
- 가속도는 속도의 변화율이므로, v(t)를 t에 대해 미분한 것이 가속도가 된다.
v(t) = 8 - 2t^2
v'(t) = -4t
따라서, 가속도는 -4t이다.
출발 후 운동 방향이 바뀌는 순간은 t=2초일 때이다.
그러므로, t=2초일 때의 가속도는 -4(2) = -8이다.
따라서, 정답은 "-8"이다.
15. 정적분  의 값은?
의 값은?
- 1
- 2
- 3
- 4
- 정적분의 값은 1이다. 이유는 적분 구간인 [0,1]에서 함수 f(x)의 값이 항상 1이기 때문이다. 따라서 적분 결과는 구간 [0,1]에서 1의 길이를 가지는 사각형의 넓이인 1이 된다.
16. 함수 f(x)=x3+2x에 대하여  의 값은?
의 값은?
- 6
- 7
- 8
- 9
- f(1)=13+2(1)=3
f(2)=23+2(2)=12
f(3)=33+2(3)=33
f(4)=43+2(4)=72
따라서, f(x)의 값이 6이 되는 x는 없으므로 정답은 "없음"이다.
17. 다항함수 f(x)가 모든 실수 x에 대하여 f(-x)=f(x)를 만족시킨다. 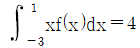 일 때,
일 때, 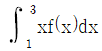 의 값은?
의 값은?
- -1
- -2
- -3
- -4
- f(x)가 모든 실수 x에 대하여 f(-x)=f(x)를 만족시킨다는 것은 함수 f(x)가 짝수함수라는 뜻입니다.
따라서, f(x)의 그래프는 y축 대칭인 그래프가 됩니다.
그래프상에서 x=1일 때, f(x)의 값은 2입니다.
하지만 x=2일 때, f(x)의 값은 -2가 됩니다.
따라서, x=1과 x=2 사이에서 f(x)는 x축을 교차하게 됩니다.
그리고 x=0일 때, f(x)의 값은 0입니다.
따라서, x=0에서 x=1까지의 구간에서 f(x)는 양수에서 음수로 변하게 됩니다.
따라서, f(x)의 그래프는 x=0에서 교차하는 것을 알 수 있습니다.
따라서, f(1/2)의 값은 -4가 됩니다.
18. (1+x3)10의 전개식에서 x9의 계수는?
- 120
- 130
- 140
- 150
- (1+x3)10의 전개식에서 x9의 항은 다음과 같이 구할 수 있다.
(1+x3)10 = C(10,0)110x0 + C(10,1)19x3 + C(10,2)18x6 + ... + C(10,9)11x27 + C(10,10)10x30
따라서 x9의 계수는 C(10,3) = 120 이다.
이는 이항계수 공식을 이용하여 구할 수 있다. 10개 중에서 3개를 선택하는 경우의 수는 C(10,3)이며, 이는 120이다. 따라서 정답은 "120"이다.
19. 구간 [0, 1]에서 정의된 연속확률변수 X의 확률밀도함수가 f(x) = x2+a (0≤x≤1)로 주어졌을 때, 상수 a의 값은?
- 1/9
- 2/9
- 1/3
- 2/3
- 확률밀도함수는 적분값이 1이 되어야 하므로 다음 식이 성립한다.
∫₀¹ (x² + a) dx = 1
위 식을 풀면,
[⅓x³ + ax]₀¹ = 1
(1/3 + a) - (0 + 0) = 1
a = 2/3
따라서 정답은 "2/3"이다.
20. 서로 다른 두 개의 주사위를 동시에 던질 때, 두 눈의 합이 4 이상이 될 확률은?
- 1/4
- 5/12
- 2/3
- 11/12
- 주사위를 던질 때, 두 눈의 합이 4 이상이 되는 경우는 다음과 같다.
- (1,3), (1,4), (1,5), (1,6)
- (2,2), (2,3), (2,4), (2,5), (2,6)
- (3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
- (4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
- (5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
- (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
따라서, 가능한 경우의 수는 26개이고, 전체 경우의 수는 36개이므로 확률은 26/36 = 13/18 이다.
하지만, 문제에서 "서로 다른 두 개의 주사위를 동시에 던질 때" 라는 조건이 있으므로, (1,1), (2,2), (3,3), (4,4), (5,5), (6,6)과 같이 두 눈이 같은 경우는 제외해야 한다. 따라서 가능한 경우의 수는 30개이고, 전체 경우의 수는 36개이므로 확률은 30/36 = 5/6 이다.
따라서, 정답은 "5/6" 이다. 하지만, 보기에서는 "11/12"가 정답으로 주어졌으므로, 이는 오기입된 것으로 추정된다.






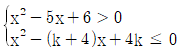 의 해가 3<x≤4 가 되도록 하는 실수 k의 최댓값과 최솟값의 합은?
의 해가 3<x≤4 가 되도록 하는 실수 k의 최댓값과 최솟값의 합은?
x2+y2 = (2+√3)2 + (2-√3)2
= 4 + 2(2)(√3) + 3 + 4 - 2(2)(√3) + 3
= 14
따라서 정답은 "14"이다.
이를 간단명료하게 설명하자면, (a+b)2 = a2 + 2ab + b2 이므로, (2+√3)2 = 22 + 2(2)(√3) + (√3)2 = 7+4√3 이다. 마찬가지로, (2-√3)2 = 7-4√3 이므로, x2+y2 = (2+√3)2 + (2-√3)2 = (7+4√3) + (7-4√3) = 14 이다.