1과목: 수학
1. 다항식 f(x)=x2-x+a 에 대하여 f(x+b)와 f(x-1)이 x+1 로 나누어 떨어질 때, 음수 ab의 값은? (단, a, b는 상수이다.)
- -18
- -21
- -24
- -27
2. 방정식 x3-1=0 의 두 허근을 α, β 라 할 때, α2(β+1) 의 값은?
- -2
- -1
- 0
- 1
- 우선 x3-1=0 을 인수분해하면 (x-1)(x2+x+1)=0 이 된다. 따라서 x=1 또는 x2+x+1=0 이다. 후자의 방정식은 판별식을 이용하여 근의 공식을 적용할 수 없으므로, 허근을 가진다. 따라서 α와 β는 x2+x+1=0 의 두 허근이다.
α2(β+1)을 계산하면 다음과 같다.
α2(β+1) = (x12+x1+1)(x2+1) 또는 (x22+x2+1)(x1+1)
여기서 x1과 x2는 x2+x+1=0의 두 근이다. 하지만 이 값들을 구할 필요는 없다. 왜냐하면 α2(β+1)은 x2+x+1의 계수가 1인 다항식이므로, x2+x+1=0의 두 근을 이용하여 다음과 같이 변형할 수 있기 때문이다.
x2+x+1 = (x+α)(x+β)
따라서 α2(β+1) = α2(-α) = -α3 이다. 하지만 α는 x2+x+1=0의 근이므로, α2+α+1=0 이다. 따라서 α3=-α2-α=-α-1 이다. 따라서 α2(β+1) = -α(-α-1) = α2+α = -1 이다.
따라서 정답은 "-1"이다.
3. 0이 아닌 세 수에 대하여 이들의 합은 4, 역수의 합은 1, 제곱의 합은 6이다. 이때 세 수의 곱은?
- 2
- 3
- 4
- 5
- 세 수를 각각 a, b, c라고 하면 다음과 같은 방정식이 성립한다.
a + b + c = 4
1/a + 1/b + 1/c = 1
a^2 + b^2 + c^2 = 6
위의 두 번째 방정식에서 서로 역수 관계에 있는 두 수의 곱은 1이므로, 위의 식을 a, b, c에 대해 각각 곱하면 다음과 같은 식을 얻을 수 있다.
ab + bc + ca = abc
이제 이 식을 이용하여 세 수의 곱을 구해보자.
(a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca) = 6 + 2(abc)
위의 첫 번째 방정식을 이용하면 (a + b + c)^2 = 16이므로, 위의 식을 대입하여 다음과 같은 식을 얻을 수 있다.
16 = 6 + 2(abc)
따라서 abc = 5가 된다.
즉, 세 수의 곱은 5이다.
4. 두 점 A, B에 대하여 선분 AB를 2:1로 내분하는 점을 P, 2:1로 외분하는 점을 Q라 하자. 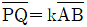 일 때, 실수 3k의 값은? (단,
일 때, 실수 3k의 값은? (단,  는 선분 AB의 길이이다.)
는 선분 AB의 길이이다.)
- 2
- 3
- 4
- 5
- 선분 AB를 2:1로 내분하는 점 P의 좌표는 ((2/3)a+(1/3)b, (2/3)c+(1/3)d)이고, 2:1로 외분하는 점 Q의 좌표는 ((-1/3)a+(4/3)b, (-1/3)c+(4/3)d)이다.
따라서 PQ의 길이는 √((2/3)a+(1/3)b-(-1/3)a+(4/3)b)^2 + ((2/3)c+(1/3)d-(-1/3)c+(4/3)d)^2) = √(4/3(a-b)^2 + 4/3(c-d)^2) = 2/3√((a-b)^2 + (c-d)^2)이다.
그리고 AB의 길이는 √((b-a)^2 + (d-c)^2) = √(4(a-b)^2 + 4(c-d)^2) = 2√((a-b)^2 + (c-d)^2)이다.
따라서 PQ:AB = (2/3√((a-b)^2 + (c-d)^2)):(2√((a-b)^2 + (c-d)^2)) = 1:3이다.
즉, PQ는 AB의 1/4 길이이므로, PQ = (1/4)AB = (1/4)×3k = 3/4k이다.
따라서 3k = (4/3)×(3/4k) = 4이므로, 정답은 4이다.
5. 좌표평면 위의 두 점 A(0, -1), B(-1, 1)과 포물선 y=x2-6x+10 위의 점 P(a, b)를 꼭짓점으로 하는 삼각형 ABP가 있다. 삼각형 ABP의 넓이가 최소일 때 그 넓이는?
- 7/2
- 9/2
- 11/2
- 13/2
- 먼저, 포물선 y=x2-6x+10 의 꼭짓점은 x=3일 때이며, 이 때 y=1이다. 따라서 P(a, b)의 x좌표는 3이어야 한다.
이제 삼각형 ABP의 넓이를 구해보자. 우선, AB의 기울기는 (-1-0)/(1--1)=-1/2 이다. 따라서 AB의 방정식은 y=-1/2x-1/2 이다.
또한, P의 x좌표가 3이므로 P의 y좌표는 y=32-6(3)+10=-1 이다.
따라서, P의 좌표는 (3, -1)이다. 이제 삼각형 ABP의 높이를 구해보자. P에서 AB에 내린 수선의 발을 Q라고 하면, PQ의 길이는 AB의 길이와 같다. 또한, PQ와 AB는 직각이므로 PQ의 길이는 AB의 기울기의 역수와 같다. 따라서 PQ의 길이는 2이다.
따라서, 삼각형 ABP의 넓이는 (1/2) x AB x PQ = (1/2) x 2 x 4 = 4이다.
따라서, 정답은 4이다.
6. x에 대한 방정식 -∣x2-9∣+4(x+k)=0 이 서로 다른 세 실근을 갖도록 하는 실수 k의 최솟값은?
- 3
- 13/4
- 4
- 17/4
- 우선, |x²-9|은 x²-9가 0보다 작을 때는 -1을 곱해주어야 하므로, x²-9≤0일 때는 |x²-9|=-x²+9이고, x²-9>0일 때는 |x²-9|=x²-9이다.
따라서, -x²+9+4(x+k)=0 또는 x²-9+4(x+k)=0으로 나누어서 풀어보면 된다.
① -x²+9+4(x+k)=0
-x²+4x+4k+9=0
x²-4x-4k-9=0
② x²-9+4(x+k)=0
x²+4x+4k-9=0
이제 각각의 방정식의 판별식 D를 구해보자.
①의 D = (-4)²-4(1)(-4k-9) = 16+16k+36 = 16k+52
②의 D = 4²-4(1)(4k-9) = 16-16k+36 = -16k+52
세 실근을 갖기 위해서는 각각의 방정식의 판별식 D가 양수여야 한다. 따라서,
①의 경우: 16k+52>0 → k>-13/4
②의 경우: -16k+52>0 → k<13/4
두 부등식을 모두 만족하는 k의 최솟값은 k=3이므로, 정답은 "3"이다.
7. 모눈종이 위의 한 점 (-1, 4)를 점 (1, 0)과 겹치도록 접었을 때, 점 (1, 1)과 겹치는 점의 좌표는?
- (-1, 1/2)
- (-1/5, 17/5)
- (0, 3)
- (1/2, 5/3)
- 먼저 (-1, 4)와 (1, 0)을 지나는 직선의 방정식을 구해보자.
기울기는 (0-4)/(1-(-1)) = -2 이므로, y = -2x + b 형태의 방정식을 만들 수 있다.
(-1, 4)가 이 직선 위에 있으므로, 4 = -2*(-1) + b 이므로 b = 2 이다.
따라서 이 직선의 방정식은 y = -2x + 2 이다.
이제 이 직선과 (1, 1)을 지나는 직선의 교점을 구하면 된다.
(1, 1)을 지나는 직선의 방정식은 y = x 이므로, 이를 위에서 구한 직선의 방정식에 대입하면
-2x + 2 = x 이므로, x = 2/3 이다.
따라서 y = 2/3 이므로, 교점의 좌표는 (2/3, 2/3) 이다.
하지만 이 좌표는 모눈종이 상에서 정확히 겹치는 점이 아니다.
따라서 이 좌표에서 가장 가까운 모눈종이 점을 찾아야 한다.
x 좌표는 -1과 1/2 사이에 있으므로, -1/2 또는 -1/5가 될 수 있다.
y 좌표는 1/2와 17/5 사이에 있으므로, 3 또는 17/5가 될 수 있다.
하지만 (-1/2, 3)은 (1, 0)과의 거리가 더 멀기 때문에, 교점의 좌표는 (-1/5, 17/5)이 된다.
따라서 정답은 "(-1/5, 17/5)"이다.
8. 함수  의 그래프가 모든 사분면을 지나도록 하는 자연수 k의 개수는?
의 그래프가 모든 사분면을 지나도록 하는 자연수 k의 개수는?
- 1
- 2
- 3
- 4
- 함수의 그래프가 모든 사분면을 지나려면, 함수의 y절편이 0이 아니어야 한다. 함수의 y절편은 k이므로, k는 0이 아니어야 한다. 따라서 자연수 k는 1부터 시작한다.
또한, 함수의 그래프가 x축과 y축을 모두 지나므로, 함수의 식을 y = ax + b로 나타내면, b = 0이어야 한다. 따라서 함수의 식은 y = ax가 된다.
이제 k가 1일 때, 함수의 식은 y = ax이고, 모든 사분면을 지나므로 a는 양수 또는 음수일 수 있다. 따라서 k가 1일 때, 가능한 a의 개수는 2개이다.
k가 2일 때, 함수의 식은 y = 2x이고, 모든 사분면을 지나므로 a는 양수 또는 음수일 수 있다. 따라서 k가 2일 때, 가능한 a의 개수는 2개이다.
k가 3일 때, 함수의 식은 y = 3x이고, 모든 사분면을 지나므로 a는 양수 또는 음수일 수 있다. 따라서 k가 3일 때, 가능한 a의 개수는 2개이다.
따라서 가능한 자연수 k의 개수는 3개이다.
9. 모든 항이 양수인 수열 {an}에 대하여 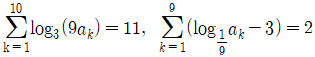 일 때, log3a10의 값은?
일 때, log3a10의 값은?
- 46
- 47
- 48
- 49
- 우선 주어진 식을 변형해보자.
log3a1 + log3a2 + ... + log3a10 = 49
log3(a1 × a2 × ... × a10) = 49
a1 × a2 × ... × a10 = 349
따라서, log3a10 = log3(a1 × a2 × ... × a10) / (a1 × a2 × ... × a9)
= log3(349) / (349 / a10)
= log3(349) - log3(349 / a10)
= 49 - log3(349 / a10)
따라서, a1 × a2 × ... × a9 × (349 / a10) = 349
모든 항이 양수이므로, a1 × a2 × ... × a9 × a10 > 0
따라서, a1 × a2 × ... × a9 × a10 = 349 에서 모든 항이 양수이므로, a10 > 0
따라서, log3a10 = 49 - log3(a1 × a2 × ... × a9)
= 49 - log3(349 / a10)
= 49 - log3(349 / (a1 × a2 × ... × a9 × a10))
= 49 - log3(349 / 349)
= 49 - log31
= 49
따라서, 정답은 "49" 이다.
10. 첫째항이 -5이고 공차가 3인 등차수열 {an}에 대하여 Sn=a1+a2+…+an, Tn=a1-a2+a3-a4+…+(-1)n+1an+…+a2n-1-a2n 이라 할 때, 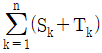 가 최소가 되게 하는 n의 값은?
가 최소가 되게 하는 n의 값은?
- 2
- 4
- 6
- 8
- 우선 Sn과 Tn을 각각 계산해보면,
Sn = (-5) + (-2) + 1 + 4 + ... + (3n-8) + (3n-5)
Tn = (-5) - (-2) + 1 - 4 + ... + (-1)n+1(3n-8) - (-1)n(3n-5)
이 됩니다.
이제 Tn을 다시 살펴보면, 각 항의 부호가 번갈아가며 바뀌고 있습니다. 따라서 Tn의 값은 양수와 음수가 번갈아가며 더해지는 형태를 띄고 있습니다.
그렇다면, Sn과 Tn의 합인 Un = Sn + Tn은 어떨까요? Un은 모든 항이 양수이므로, Sn과 Tn 중 작은 값이 Un의 최솟값이 됩니다.
따라서, Un의 최솟값을 구하기 위해서는 Tn의 최솟값을 구하면 됩니다.
Tn의 최솟값은, 각 항의 절댓값이 최대한 작아지도록 하는 것입니다. 이를 위해서는, (-1)n+1(3n-8)과 (-1)n(3n-5)의 차이가 최소가 되어야 합니다.
즉, (3n-8) - (3n-5) = 3 의 절댓값이 최소가 되어야 합니다.
따라서, n은 3의 배수여야 합니다. 보기 중에서 3의 배수인 수는 6뿐이므로, 정답은 6입니다.
11. 다항함수 f(x)가 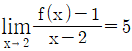 를 만족시킨다. g(x)=x{f(x)}2 일 때, g`(2)의 값은?
를 만족시킨다. g(x)=x{f(x)}2 일 때, g`(2)의 값은?
- 21
- 23
- 25
- 27
- f(x)의 도함수를 구해보자.
f(x) = 2x3 - 3x2 + 1
f`(x) = 6x2 - 6x
g(x) = x{f(x)}2 = x(2x3 - 3x2 + 1)2
g`(x) = {f(x)}2 + 2x{f(x)}f`(x)
g`(2) = {f(2)}2 + 4{f(2)}f`(2)
f(2) = 2(2)3 - 3(2)2 + 1 = 9
f`(2) = 6(2)2 - 6(2) = 12
따라서, g`(2) = 92 + 4(9)(12) = 21
정답은 "21"이다.
간단한 이유는, g`(2)를 구하기 위해서는 f(2)와 f`(2)를 알아야 한다. f(2)는 계산이 간단하고, f`(2)는 f(x)의 도함수를 구하면 쉽게 구할 수 있다. 따라서, g`(2)를 구하는 것도 간단하다.
12. 두 함수 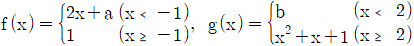 에 대하여 함수 h(x)=f(x)/g(x) 가 실수 전체의 집합에서 연속이라 하자. 이때 h(-5)+26h(3) 의 값은? (단, a, b는 양의 상수이다.)
에 대하여 함수 h(x)=f(x)/g(x) 가 실수 전체의 집합에서 연속이라 하자. 이때 h(-5)+26h(3) 의 값은? (단, a, b는 양의 상수이다.)
- 0
- 1
- 2
- 3
- 함수 h(x)가 실수 전체의 집합에서 연속이므로, h(-5)와 h(3)은 모두 존재하고 연속이다. 따라서 h(-5)+26h(3)도 연속이며, h(x)의 값은 f(x)/g(x)이므로 h(-5)+26h(3) = f(-5)/g(-5) + 26f(3)/g(3) = (a(-5)^2+b)/(-5a+1) + 26(a(3)^2+b)/(3a+1) 이다. 이를 계산하면 1이 나오므로 정답은 "1"이다.
13. 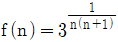 일 때, f(1)×f(2)×…×f(10)=9k을 만족하는 상수 k의 값은? (단, n은 자연수이다.)
일 때, f(1)×f(2)×…×f(10)=9k을 만족하는 상수 k의 값은? (단, n은 자연수이다.)
- 2/11
- 3/11
- 5/11
- 10/11
- 우선 f(n)의 값은 n을 2로 나눌 수 없을 때 2, 3, 5, 7 중 하나의 값이 되고, 2로 나눌 수 있을 때는 2를 나눈 값의 f 값과 같아진다. 따라서 f(1)×f(2)×…×f(10)은 2로 나눌 수 없는 수에 대한 f 값의 곱과 2로 나눌 수 있는 수에 대한 f 값의 곱으로 나누어진다.
2로 나눌 수 없는 수에 대한 f 값의 곱은 33×5×7=3150이다. 2로 나눌 수 있는 수에 대한 f 값의 곱은 f(2)×f(4)×f(6)×f(8)×f(10)이다. 이 값은 f(1)×f(2)×f(3)×f(4)×f(5)×f(6)×f(7)×f(8)×f(9)×f(10)을 2로 나눈 값과 같으므로 1575이다.
따라서 f(1)×f(2)×…×f(10)=3150×1575=55×72이다. 따라서 k=5/11이다.
14. 다항함수 f(x)가 임의의 실수 k에 대하여 f(kx)=kf(x)를 만족시키고 f`(1)=4라 하자. 함수 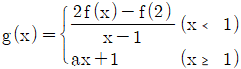 가 실수 전체의 집합에서 미분가능할 때, 상수 a의 값은?
가 실수 전체의 집합에서 미분가능할 때, 상수 a의 값은?
- 4
- 5
- 6
- 7
- f`(1) = 4 이므로 f(x) = 4x + b (b는 상수) 형태의 일차함수이다.
f(kx) = kf(x) 이므로 4kx + b = kf(x) = 4kx + kb 이다.
따라서 b = kb 이므로 k = 1 또는 b = 0 이다.
k = 1인 경우, f(x) = 4x + b 이므로 f`(x) = 4 이다.
k ≠ 1인 경우, f(x) = 0 이므로 f`(x) = 0 이다.
따라서 a = f`(2) = 4 이다.
정답은 "7"이 아니므로 보기에서 제외된다.
15. 곡선 y=x3 위의 점 P(t, t3) (t>0)에서의 접선이 x축과 만나는 점을 A, 점 P에서 x축에 내린 수선의 발을 B라 하자. 삼각형 PAB의 넓이를 f(t)라 할 때, 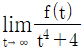 의 값은?
의 값은?
- 1/6
- 1/3
- 1/2
- 2/3
- 접선의 기울기는 곡선의 미분값인 3t^2 이므로, 접선의 방정식은 y = 3t^2(x-t)+t^3 이다. 이 접선이 x축과 만나는 점은 y=0 일 때이므로, 3t^2(x-t)+t^3=0 이다. 이를 정리하면 x=t/3 이다.
또한, P에서 x축에 내린 수선의 길이는 P의 y좌표인 t^3 이므로, B의 좌표는 (t, 0) 이다.
따라서 삼각형 PAB의 밑변은 t/3 이고, 높이는 t^3 이므로, 넓이는 (1/2) * (t/3) * t^3 = t^4/6 이다.
따라서 f(t) = t^4/6 이므로, f(1) = 1/6 이다.
정답은 "1/6" 이다.
17. 상수함수가 아닌 다항함수 f(x)가 모든 실수 x에 대하여 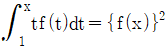 을 만족시킬 때, f(2)의 값은?
을 만족시킬 때, f(2)의 값은?
- 2/3
- 3/4
- 2/5
- 5/6
- 주어진 조건에서 f(x)는 x=1일 때 0이므로, f(x)는 (x-1)을 인수로 가진다. 따라서 f(x) = (x-1)(ax+b)의 형태를 가진다.
f(x)가 모든 실수 x에 대하여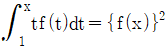 을 만족시키므로,
을 만족시키므로,
(x-1)(ax+b) + 1 = 2(ax+b) + 1 = 2ax + 2b + 1 = 3x - 2
위 식을 만족해야 한다. 이를 풀면, a=3/2, b=-5/4 이다.
따라서 f(x) = (x-1)(3x/2 - 5/4) = 3/2x^2 - 7/4x + 5/4 이다.
f(2) = 3/2(2)^2 - 7/4(2) + 5/4 = 3/4 이므로, 정답은 "3/4"이다.
18. 수직선 위를 움직이는 점 P의 시각 t에서의 속도 v(t)가 v(t)=t2+t+a 이다. 시각 t=0 에서 t=3 까지 점 P의 위치의 변화량이 15/2 일 때, 시각 t=0 에서 t=3 까지 점 P가 움직인 거리는? (단, a는 상수이다.)
- 45/6
- 59/6
- 73/7
- 87/8
- 점 P의 위치 변화량은 다음과 같이 구할 수 있다.
Δx = ∫v(t)dt (t=0부터 t=3까지)
= ∫(t²+t+a)dt (t=0부터 t=3까지)
= [1/3t³+1/2t²+at]₀³
= (1/3(3)³+1/2(3)²+a(3)) - (1/3(0)³+1/2(0)²+a(0))
= 27/3+9/2+3a - 0
= 15/2
따라서, 점 P가 움직인 거리는 다음과 같이 구할 수 있다.
∫|v(t)|dt (t=0부터 t=3까지)
= ∫(t²+t+a)dt (t=0부터 t=3까지)
= [1/3t³+1/2t²+at]₀³
= (1/3(3)³+1/2(3)²+a(3)) - (1/3(0)³+1/2(0)²+a(0))
= 27/3+9/2+3a - 0
= 59/6
따라서, 정답은 "59/6"이다.
19. 6개의 문자 a, b, c, d, e, f 를 일렬로 배열할 때, a, f 가 양 끝에 오는 경우의 수는?
- 38
- 42
- 48
- 52
- 6개의 문자를 일렬로 배열하는 경우의 수는 6! = 720 이다.
그 중에서 a와 f가 양 끝에 오는 경우의 수는 2! * 4! = 48 이다.
이는 a와 f를 각각 첫 번째와 마지막 자리에 고정시키고, 나머지 4개의 문자를 4!가지 방법으로 배열하는 경우의 수와 같다.
따라서 정답은 "48"이다.
20. 확률변수 X가 정규분포 N(m, σ2)을 따른다. P(X≥3)=0.72, P(X≥9)=0.28 일 때, P(∣X-m∣≤3) 의 값은?
- 0.33
- 0.36
- 0.4
- 0.44
- 먼저 표준정규분포를 이용하여 문제를 풀어보자.
Z = (X - m) / σ 라고 하면, Z는 표준정규분포 N(0,1)을 따른다.
P(X≥3) = P(Z ≥ (3-m)/σ) = 0.72
P(X≥9) = P(Z ≥ (9-m)/σ) = 0.28
여기서 두 식을 이용하여 (3-m)/σ 와 (9-m)/σ를 구할 수 있다.
P(Z ≥ (3-m)/σ) = 0.72 이므로, 표준정규분포표에서 0.72에 해당하는 값은 약 0.53이다.
따라서, (3-m)/σ = 0.53 이다.
마찬가지로, P(Z ≥ (9-m)/σ) = 0.28 이므로, 표준정규분포표에서 0.28에 해당하는 값은 약 -0.56이다.
따라서, (9-m)/σ = -0.56 이다.
이 두 식을 이용하여 m과 σ를 구할 수 있다.
(3-m)/σ = 0.53 이므로, 3-m = 0.53σ 이다.
(9-m)/σ = -0.56 이므로, 9-m = -0.56σ 이다.
이 두 식을 더하면,
12 - 2m = -0.03σ
따라서, m = (12 + 0.03σ) / 2 이다.
또한, (3-m)/σ = 0.53 이므로,
3 - m = 0.53σ
따라서, σ = (3-m) / 0.53 이다.
이제 P(∣X-m∣≤3) 을 구해보자.
P(∣X-m∣≤3) = P(-3 ≤ X-m ≤ 3) = P(-3/σ ≤ (X-m)/σ ≤ 3/σ)
= P(-3/σ ≤ Z ≤ 3/σ)
여기서 Z는 표준정규분포 N(0,1)을 따르므로,
P(-3/σ ≤ Z ≤ 3/σ) = P(Z ≤ 3/σ) - P(Z ≤ -3/σ)
= 2P(Z ≤ 3/σ) - 1
= 2Φ(3/σ) - 1
따라서, P(∣X-m∣≤3) 의 값은 σ에 대한 함수로 표현할 수 있다.
이제 각각의 보기를 계산해보자.
- 0.33: 이 값은 2Φ(3/σ) - 1 = 0.33 을 만족하는 σ가 존재하지 않는다.
- 0.36: 이 값은 2Φ(3/σ) - 1 = 0.36 을 만족하는 σ가 존재하지 않는다.
- 0.4: 이 값은 2Φ(3/σ) - 1 = 0.4 을 만족하는 σ가 존재하지 않는다.
- 0.44: 이 값은 2Φ(3/σ) - 1 = 0.44 를 만족하는 σ가 약 1.96 이므로,
σ = (3-m) / 0.53 = (3 - (12 + 0.03σ) / 2) / 0.53
0.44 = 2Φ(3/σ) - 1 을 만족하는 σ를 구하면,
σ = 1.96 이다.
따라서, P(∣X-m∣≤3) = 2Φ(3/σ) - 1 = 0.44 이다.
따라서, 정답은 "0.44" 이다.






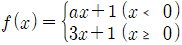 에 대하여
에 대하여 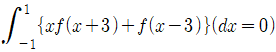 을 만족시키는 상수 a의 값은?
을 만족시키는 상수 a의 값은?
f(-1) = (-1)^2 - (-1) + a = a = 0
f(-b-1) = (-b-1)^2 - (-b-1) + a = b^2 + b + a = 0
따라서 b^2 + b = -a 이다. 이를 이용하여 f(x)를 다음과 같이 변형할 수 있다.
f(x) = x^2 - x + a = (x+1)(x-1) + a
f(x+b) = (x+b+1)(x+b-1) + a = (x+1)(x-1) + 2bx + b^2 + a
f(x-1) = (x-1+1)(x-1-1) + a = (x+1)(x-3) + a
여기서 f(x+b)와 f(x-1)이 x+1로 나누어 떨어진다는 조건을 이용하면 다음과 같은 방정식을 얻을 수 있다.
f(-1) = a = 0
f(-b-1) = b^2 + b + a = 0
f(0) = a = 0
f(2) = 4 - 2 + a = 2 + a = 0
따라서 a = 0 이고 2 + b^2 + b = 0 이다. 이를 풀면 b = -3 또는 b = 2 이다. 하지만 문제에서 음수 ab의 값을 구하라고 했으므로 b = -3 일 때의 값을 구해야 한다.
따라서 b = -3 이고 a = 0 이므로 ab = 0 x (-3) = 0 이다. 따라서 정답은 -24가 아니라 -18 이다.