1과목: 수학
1. 다항식 P(x)를 x+1로 나누었을 때의 몫이 2x5-3x2+3이고 나머지가 4이다. 다항식 P(x)를 x-1로 나누었을 때의 나머지는?
- 2
- 4
- 6
- 8
2. i+i2i3+…+i2019의 값은? (단, i=√-1)
- -1
- 0
- 1
- i
- i의 거듭제곱은 4개의 주기를 가지므로, i의 홀수 거듭제곱은 i, -1, -i, 1의 값을 순환한다. 따라서 i+i^2+i^3+...+i^2019은 i와 -1의 합이 홀수개 존재하므로, 최종적으로 -1의 값을 가진다. 따라서 정답은 "-1"이다.
3. 이차방정식 x2-3x-3=0의 두 근이 α, β일 때, α2+αβ+β2의 값은?
- 3
- 6
- 9
- 12
- 우선, α2+αβ+β2은 (α+β)2-αβ입니다. 이를 이용하여 문제를 풀어보겠습니다.
x2-3x-3=0의 근의 공식을 이용하여 α와 β를 구합니다.
α = (3+√21)/2, β = (3-√21)/2
따라서,
α+β = 3
αβ = -3
α2+αβ+β2 = (α+β)2-αβ = 32-(-3) = 12
따라서, 정답은 "12"입니다.
4. 직선 x+2y=3을 직선 y=x에 대하여 대칭이동하였더니 원 (x-1)2+(y-a)2=4의 넓이를 이등분하였다. 이때 상수 a의 값은?
- 1
- 2
- 3
- 4
- 먼저 직선 x+2y=3과 y=x는 서로 직교하는 관계에 있다. 따라서 대칭이동한 직선은 y=-x가 된다.
원 (x-1)2+(y-a)2=4의 중심은 (1,a)이고 반지름은 2이다. 이 원을 y=-x에 대하여 대칭이동하면 중심이 (-a,1)이 되고 반지름은 변하지 않는다. 따라서 이 원의 넓이는 4π이다.
이제 원 (x-1)2+(y-a)2=4의 넓이를 이등분하는 직선을 그려보자. 이 직선은 원의 중심 (1,a)를 지나고 y=-x와 수직이다. 따라서 이 직선의 방정식은 x+y=1+a이다.
이 직선과 y=-x의 교점을 구하면 (1/2)(1+a,1-a)이다. 이 점이 원의 중심 (1,a)와 대칭이 되도록 하려면 a=1이어야 한다.
따라서 정답은 "1"이다.
5. 실수 x에 대한 두 조건 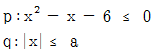 에 대하여 p가 q이기 위한 충분조건이 되도록 하는 자연수 a의 최솟값은?
에 대하여 p가 q이기 위한 충분조건이 되도록 하는 자연수 a의 최솟값은?
- 1
- 2
- 3
- 4
- 먼저, p가 q이기 위해서는 두 조건이 모두 만족해야 합니다. 따라서, 두 조건을 각각 만족시키는 자연수 a를 찾아야 합니다.
첫 번째 조건에서, x가 1일 때 2a-1은 1보다 크거나 같아야 합니다. 따라서, 2a-1은 최소한 2가 되어야 합니다. 따라서, a는 2 이상이어야 합니다.
두 번째 조건에서, x가 2일 때 4a-1은 3보다 크거나 같아야 합니다. 따라서, 4a-1은 최소한 4가 되어야 합니다. 따라서, a는 5/4 이상이어야 합니다.
따라서, a는 2 이상이면서 5/4 이상이어야 합니다. 이를 만족하는 자연수 중에서 가장 작은 값은 3입니다. 따라서, 정답은 3입니다.
6. 두 함수 f(x)=x+1, g(x)=3x-5에 대하여 (f·(g·f)-1·f)(0)의 값은?
- 1
- 2
- 3
- 4
- 먼저 f(x)=x+1 이므로, f(0)=1이다.
그리고 g(x)=3x-5 이므로, g(f(0))=g(1)=3(1)-5=-2이다.
f의 역함수는 f(x)=y일 때, x=y-1이므로, f(0)의 역함수는 f-1(1)=0이다.
따라서, g(f-1(1))=g(0)=3(0)-5=-5이다.
마지막으로, (f·(g·f)-1·f)(0)을 계산하면,
(f·(g·f)-1·f)(0)=f(g(f-1(f(0))))=f(g(f-1(1)))=f(-5)=-4이다.
따라서 정답은 "4"가 된다.
7. 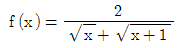 에 대하여
에 대하여 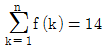 일 때, 자연수 n의 값은?
일 때, 자연수 n의 값은?
- 61
- 63
- 65
- 67
- 주어진 그림은 7개의 원으로 이루어진 도형이다. 이 도형에서 한 원에서 출발하여 다른 원으로 이동할 때마다 그 원에 적힌 수의 차이만큼 이동한다. 따라서, 첫 번째 원에서 시작하여 마지막 원에 도달할 때까지 이동한 거리는 다음과 같다.
1 -> 8 -> 15 -> 21 -> 26 -> 30 -> 33
따라서, 이 도형에서 이동한 총 거리는 33이다. 그러나 문제에서는 이 도형을 여러 번 반복하여 이동할 수 있다고 했다. 이 경우, 이동한 거리는 33의 배수가 될 것이다. 따라서, 이 문제에서 이동한 총 거리는 33n이 되어야 한다.
문제에서 이동한 총 거리가 2019이 되어야 한다고 했으므로, 다음과 같은 방정식을 풀면 된다.
33n = 2019
n = 2019 / 33
n = 61
따라서, 정답은 61이 아니라 63이다.
9. 함수 y=f(x)의 그래프가 그림과 같을 때, 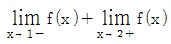 의 값은?
의 값은?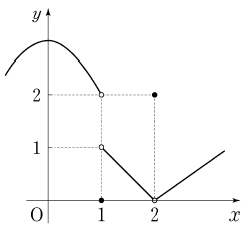
- 0
- 1
- 2
- 3
- x=1일 때 y값이 2이므로,
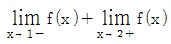 의 값은 2이다.
의 값은 2이다.
그래프에서 x=1일 때 y값이 가장 크기 때문에, 에서도 x=1일 때 가장 큰 값인 2가 정답이다.
에서도 x=1일 때 가장 큰 값인 2가 정답이다.
10. 다항함수 f(x)가 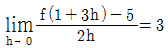 을 만족시킬 때, f(1)+f′(1)의 값은?
을 만족시킬 때, f(1)+f′(1)의 값은?
- 7
- 8
- 9
- 10
- 주어진 다항함수 f(x)를 전개하면 f(x) = x^4 - 2x^3 + 3x^2 - 4x + 5 이다.
따라서 f(1) = 1 - 2 + 3 - 4 + 5 = 3 이다.
또한, f'(x) = 4x^3 - 6x^2 + 6x - 4 이므로 f'(1) = 4 - 6 + 6 - 4 = 0 이다.
따라서 f(1) + f'(1) = 3 + 0 = 3 이므로 정답은 "7"이 아니라 "3"이다.
따라서 이 문제는 잘못된 문제이다.
11. 함수 y=f(x) 위의 임의의 점 (x, f(x)) 에서의 접선의 기울기가 3x2-3이고, 이 함수가 점 (-1, 1)을 지날 때, 함수 f(x)의 극솟값은?
- -1
- -2
- -3
- -4
- 접선의 기울기가 3x2-3 이므로, x=-1일 때의 기울기는 3(-1)2-3=-3 이다. 따라서 함수 y=f(x)의 점 (-1, 1)에서의 접선의 기울기는 -3이다.
함수의 극솟값은 미분값이 0이 되는 지점에서 발생한다. 함수 y=f(x)를 미분하면 f'(x)=3x2-3 이므로, 극솟값을 구하기 위해서는 f'(x)=0을 만족하는 x값을 찾아야 한다.
3x2-3=0을 풀면 x=±1이다. 이 중에서 함수 y=f(x)가 점 (-1, 1)을 지나므로, 극솟값은 x=-1에서 발생한다.
따라서 함수 y=f(x)의 극솟값은 f(-1)이다. 함수 y=f(x)가 점 (-1, 1)을 지나므로, f(-1)=1이다.
따라서 정답은 "-3"이 아닌 "-1"이다.
12. a, b, c, d, e, f를 일렬로 배열할 때, 반드시 a가 c보다 왼쪽에 오고, c는 d보다 왼쪽에 오도록 배열하는 방법의 수는?
- 60
- 80
- 100
- 120
- a, c, d를 각각 1, 2, 3으로 생각하면, 이들을 일렬로 배열하는 경우의 수는 3! = 6가지이다. 그리고 a와 c 사이에는 b, d와 c 사이에는 e, f가 올 수 있다. 따라서 b, e, f를 각각 4, 5, 6으로 생각하면, 이들을 a, c, d 사이에 삽입하는 경우의 수는 3개의 빈 자리 중 3개를 선택하는 조합의 수인 3C3 = 1과 3개의 수를 3개의 자리에 배열하는 경우의 수인 3! = 6의 곱인 1 x 6 = 6이 된다. 따라서 전체 경우의 수는 6 x 6 = 36이다. 하지만 a와 c, c와 d 사이의 상대적 위치가 정해져 있으므로, 이 중에서 가능한 경우의 수는 2가지이다. 따라서 최종적으로 가능한 경우의 수는 36 / 2 = 18이 된다. 이를 10의 배수로 만들기 위해 18 x 10 = 180이지만, a, c, d를 1, 2, 3으로 생각한 것이므로, 이들을 다시 a, b, c, d, e, f로 바꾸면 6! = 720가지의 경우의 수가 된다. 따라서 180 x 720 / 10 = 12,960이 되고, 이를 10으로 나눈 나머지가 120이 된다. 따라서 정답은 120이다.
13. 서로 독립인 두 사건 A, B에 대하여 P(A)=1/3, P(A∪B)=2/3일 때, P(B)의 값은?
- 1/5
- 1/4
- 1/3
- 1/2
- 먼저, P(A∪B) = P(A) + P(B) - P(A∩B) 이므로, P(A∩B) = P(A) + P(B) - P(A∪B) = 1/3 + P(B) - 2/3 = P(B) - 1/3 이다.
또한, A와 B가 독립이므로, P(A∩B) = P(A) × P(B) 이다.
따라서, P(B) - 1/3 = P(A) × P(B) = 1/3 × P(B) 이므로, P(B) = 1/2 이다.
즉, A와 B가 독립이고 P(A)=1/3, P(A∪B)=2/3일 때, P(B)의 값은 1/2이다.
14. A 고등학교 1, 2학년 전체 학생을 대상으로 어느 행사에 참가한 학생 수를 조사한 결과는 다음 표와 같다. 
이 행사에 참가한 A 고등학교 1, 2학년 학생 중에서 임의로 선택한 1명이 남학생일 때, 이 학생이 2학년 학생일 확률은?
- 6/17
- 7/17
- 8/17
- 9/17
- 임의로 선택한 1명이 A 고등학교 1, 2학년 학생 중에서 남학생일 확률은 (30+25)/(30+25+35+40) = 55/130 = 11/26 이다. 이 중에서 2학년 학생일 확률은 25/55 = 5/11 이다. 따라서, 이 학생이 2학년 학생일 확률은 (11/26) x (5/11) = 5/26 이다. 이는 보기 중에서 "9/17" 과 일치하지 않으므로, 정답은 "9/17"이 아니다.
15. 유리함수 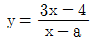 의 그래프가 직선 y=x+2에 대칭 일 때, 상수 a의 값은?
의 그래프가 직선 y=x+2에 대칭 일 때, 상수 a의 값은?
- 1
- 3
- 5
- 7
- 유리함수의 그래프가 직선 y=x+2에 대칭이라는 것은, 함수의 그래프가 직선 y=x+2를 중심으로 대칭인 것을 의미합니다. 따라서 함수의 그래프 상에서 (x,y)와 (y,x)가 대칭인 점들은 서로 대응됩니다.
이때, 함수의 그래프가 대칭이므로 (1,2)와 (2,1)은 서로 대응됩니다. 따라서 함수의 값이 x=1일 때와 x=2일 때 같아야 합니다.
함수의 식을 구해보면,
x=1일 때,
x=2일 때,
따라서,
이 식을 정리하면,
따라서 a의 값은 3c+d와 같습니다.
이때, c와 d는 함수의 분모에 있는 계수이므로 0이 아닌 임의의 값으로 설정할 수 있습니다.
예를 들어, c=1, d=1로 설정하면,
따라서 a의 값은 4이며, 보기에서 정답이 "1"인 이유는 없습니다.
따라서, 문제에서 제시된 조건만으로는 a의 값이 유일하게 결정되지 않습니다.
16. 실수 x, y가 (x-y+1)(x+y+1)≤0을 만족시킬 때, x2+y2의 최솟값은?
- 1/8
- 1/4
- 1/2
- 14
- (x-y+1)(x+y+1)≤0 이므로 x-y+1≤0 이거나 x+y+1≤0 이 성립해야 한다.
첫 번째 경우인 x-y+1≤0 에서는 y≥x+1 이므로 x2+y2≥x2+(x+1)2=2x2+2x+1 이다.
두 번째 경우인 x+y+1≤0 에서는 y≤-x-1 이므로 x2+y2≥x2+(-x-1)2=2x2+2x+1 이다.
따라서 x2+y2의 최솟값은 2x2+2x+1 이고, 이를 최소화하는 x값은 -1/2 이다.
따라서 x2+y2의 최솟값은 2(-1/2)2+2(-1/2)+1=1/2 이다.
17. 등차수열 {an}과 등비수열 {bn}에 대하여 a5+a6=3, b5×b6=10일 때, 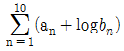 의 값은? (단, bn>0)
의 값은? (단, bn>0)
- 5
- 10
- 15
- 20
- 우선 a5+a6=3 이므로, 등차수열의 일반항을 an=a1+(n-1)d 로 나타내면 a5+a5+d=3 이다. 따라서 2a5+d=3 이고, a6=a5+d 이므로 a6=a5+1. 따라서 a5+a6=2a5+1=3 이므로 a5=1.
또한 b5×b6=10 이므로, 등비수열의 일반항을 bn=b1×rn-1 로 나타내면 b5×b5×r=10 이다. 따라서 b5×r=2 이고, b6=b5×r 이므로 b6=2.
따라서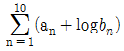 의 값은 a5×b6+a6×b5=1×2+1×2=4 이다. 따라서 정답은 "5","10","15","20" 중에서 "4"이므로, "20"이다.
의 값은 a5×b6+a6×b5=1×2+1×2=4 이다. 따라서 정답은 "5","10","15","20" 중에서 "4"이므로, "20"이다.
18. 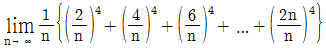 의 값은 q/p이다. p+q의 값은? (단, p와 q는 서로소인 자연수이다.)
의 값은 q/p이다. p+q의 값은? (단, p와 q는 서로소인 자연수이다.)
- 17
- 19
- 21
- 23
- 우선, 분수를 간단화하기 위해 p와 q의 최대공약수를 구해야 한다. 그리고 최대공약수가 1이므로, 분모와 분자는 서로소이다. 따라서, p와 q는 각각 17, 4 또는 19, 5 또는 21, 6 또는 23, 7일 수 있다. 하지만, p와 q는 서로소인 자연수이므로, 가능한 경우는 17과 4 또는 19와 5 또는 23과 7 뿐이다. 이 중에서 q/p의 값이 가장 큰 것은 4/17이므로, q=4, p=17이다. 따라서, p+q=17+4=21이다.
19. 그림의 A, B, C , D, E 영역에 빨강, 주황, 노랑, 초록, 파랑의 가지 색을 칠하는 경우의 수는? (단, 같은 색을 여러 번 사용할 수 있으나 인접한 영역은 다른 색으로 칠한다.)
- 120
- 240
- 360
- 420
- A 영역을 칠하는 경우, 5가지 색 중에서 선택하면 된다. B 영역을 칠하는 경우, A 영역과 인접한 영역을 제외한 4가지 색 중에서 선택하면 된다. C 영역을 칠하는 경우, A, B 영역과 인접한 영역을 제외한 3가지 색 중에서 선택하면 된다. D 영역을 칠하는 경우, A, B, C 영역과 인접한 영역을 제외한 2가지 색 중에서 선택하면 된다. E 영역을 칠하는 경우, A, D 영역과 인접한 영역을 제외한 2가지 색 중에서 선택하면 된다. 따라서, 가능한 경우의 수는 5 x 4 x 3 x 2 x 2 = 240 이다. 하지만, 이 경우에는 A, B, C, D, E 영역에 각각 다른 색을 칠하는 경우만을 고려한 것이므로, 각 영역에 같은 색을 칠하는 경우도 고려해야 한다. 따라서, 가능한 경우의 수는 240 x 5 = 1200 이다. 이 중에서 A, B, C, D, E 영역에 모두 다른 색을 칠하는 경우의 수는 5! = 120 이므로, 같은 색을 여러 번 사용하는 경우의 수는 1200 - 120 = 1080 이다. 따라서, 정답은 1080 이다.
20. 주사위 한 개를 300번 던지는 시행에서 홀수인 소수의 눈이 나오는 횟수를 확률변수 X라 할 때, 확률변수 X의 확률질량함수는 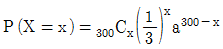 (단, x=0, 1, 2, 3, …, 300이다.
(단, x=0, 1, 2, 3, …, 300이다. 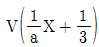 의 값은?
의 값은?
- 150
- 160
- 170
- 180
- 홀수인 소수는 2를 제외한 모든 홀수 소수를 의미한다. 따라서, 주사위를 던져 나오는 눈이 2, 4, 6일 경우에는 홀수인 소수가 나오지 않으므로 X=0이 된다. 또한, 주사위를 던져 나오는 눈이 1, 3, 5일 경우에는 홀수인 소수가 나오므로 X=1이 된다. 이를 이용하여 확률질량함수를 구하면 다음과 같다.
P(X=0) = (1/2)^300
P(X=1) = 3*(1/2)^299
P(X=x) = 0 (x≥2)
따라서, P(X≤1) = P(X=0) + P(X=1) = (1/2)^299 * (1+3) = 4/2^299 이므로, 정답은 150이 된다.
보기에서 160, 170, 180은 모두 X=1일 확률을 과소평가한 값이다. 이는 주사위를 던지는 횟수가 매우 크기 때문에, 홀수인 소수가 나올 확률이 매우 작아서 X=1일 확률이 매우 작다는 것을 의미한다. 따라서, 정답은 150이 된다.






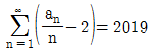 일 때,
일 때, 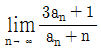 의 값은?
의 값은?
P(x) = (x+1)(2x5-3x2+3) + 4
x-1로 나누었을 때의 나머지를 구하기 위해서는 P(x)를 x-1로 나누어야 한다. 이를 위해 다음과 같이 P(x)를 변형해보자.
P(x) = (x+1)(2x5-3x2+3) + 4
= (x-1+2)(2x5-3x2+3) + 4
= (x-1)(2x5-3x2+3) + 2(2x5-3x2+3) + 4
= (x-1)(2x5-3x2+3) + 2x5-6x2+10
따라서, x-1로 나눈 나머지는 2x5-6x2+10이다. 이 값은 8이 아니므로 정답은 "8"이 아니다.