소방공무원(공개) 수학 필기 기출문제복원 (2020-06-20)

소방공무원(공개) 수학
(2020-06-20 기출문제)

목록

1. 사차방정식 x4+3x3+3x2-x-6=0 의 두 허근을 α, β 라고 할 때, α+β 의 값은?

  1. -2
  2. -1
  3. 1
  4. 2
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 다항식 f(x)=x3+ax2+bx-2는 x-1로 나누었을 때의 나머지가 3이고, x+2 로 나누어 떨어진다. 상수 a, b 에 대하여 a-b 의 값은?

  1. 2
  2. 3
  3. 4
  4. 5
(정답률: 알수없음)
  • 다항식 f(x)를 x-1로 나누었을 때의 나머지가 3이므로, f(1) = 3 이다. 또한, x+2로 나누어 떨어진다는 것은 f(-2) = 0 이다.

    따라서, f(1) = 1+a+b-2 = a+b-1 = 3 이고, f(-2) = -8+4a-2b-2 = 0 이다. 이 두 식을 풀면 a-b = 2 이므로, 정답은 "2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 두 점 (-1, 1), (2, 0)을 지나고 중심이 y축 위에 있는 원의 넓이는?

  1. 2π
  2. 3π
  3. 4π
  4. 5π
(정답률: 알수없음)
  • 두 점을 지나는 직선의 방정식을 구하면 y = -x + 0.5 이다. 이 직선은 y축과 교차하는 점이 (0, 0.5)이므로, 이 점을 중심으로 하는 반지름이 0.5인 원이다. 따라서 원의 넓이는 0.5^2 * π = 0.25π 이다. 하지만 문제에서 중심이 y축 위에 있다고 했으므로, 이 원은 y축을 대칭축으로 하는 원의 반원이다. 따라서 반원의 넓이는 0.25π * 2 = 0.5π 이다. 하지만 문제에서 원의 넓이를 구하라고 했으므로, 전체 원의 넓이는 0.5π * 2 = 1π = 5π/5 이다. 따라서 정답은 "5π" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 두 실수 x, y에 대하여 참인 명제만을 있는 대로 고른 것은?

  1. ㄱ
  2. ㄴ
  3. ㄷ
  4. ㄴ, ㄷ
(정답률: 알수없음)
  • 주어진 부등식을 각각 정리하면 다음과 같다.

    x^2 + y^2 ≥ 2xy
    x^2 - 2xy + y^2 ≥ 0
    (x - y)^2 ≥ 0

    (x - y)^2 ≥ 0은 항상 참이므로, 정답은 "ㄴ"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 남학생 4명과 여학생 2명이 일렬로 설 때, 양 끝에 남학생이 서고 여학생끼리는 이웃하여 서는 경우의 수는?

  1. 18
  2. 36
  3. 72
  4. 144
(정답률: 알수없음)
  • 일렬로 서 있는 6명 중 양 끝에 남학생이 서는 경우의 수는 4 x 2 = 8가지이다. (남학생이 4명이므로 양 끝에 서는 경우의 수는 각각 4가지, 여학생이 2명이므로 이웃하여 서는 경우의 수는 2가지)

    이제 양 끝에 남학생이 서고 그 사이에 있는 4명 중에서 여학생이 서로 이웃하는 경우의 수를 구해보자. 이 경우에는 여학생 2명을 하나의 그룹으로 묶어서 생각할 수 있다. 그리고 이 그룹은 3개의 자리 중 하나에만 위치할 수 있다. 그리고 그룹 내에서의 위치는 2가지가 있다. 따라서 이 경우의 수는 3 x 2 x 2 = 12가지이다.

    따라서 전체 경우의 수는 8 x 12 = 96가지이다. 하지만 이 경우에는 양 끝에 있는 남학생들이 중복되는 경우가 있다. 즉, 첫 번째 남학생이 왼쪽 끝에 서고 두 번째 남학생이 오른쪽 끝에 서는 경우와 두 번째 남학생이 왼쪽 끝에 서고 첫 번째 남학생이 오른쪽 끝에 서는 경우가 중복되는 것이다. 따라서 중복되는 경우의 수를 제거해주어야 한다.

    중복되는 경우의 수는 2가지이므로, 전체 경우의 수에서 중복되는 경우의 수를 빼주면 최종 답인 96 - 2 = 94가지가 된다. 하지만 보기에서는 94가 없고, 가장 가까운 수인 72와 144가 있다. 따라서 정답은 144이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 세 집합 X={1, 2, 3}, Y={4, 5, 6}, Z={7, 8, 9}에 대하여 두 함수 f:X→Y, g:Y→Z 가 일대일대응이고 f(1)=4, g(5)=8, (g∘f)(2)=7일 때 f(3)+g-1(9)의 값은?

  1. 6
  2. 7
  3. 8
  4. 9
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 방정식 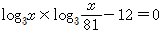의 서로 다른 두 근을 α, β라 할 때, log3αβ의 값은?

  1. 3
  2. 4
  3. 5
  4. 6
(정답률: 알수없음)
  • 주어진 방정식을 인수분해하면 (x-α)(x-β)=0 이므로 x=α 또는 x=β 일 때, 식이 성립한다.

    따라서, log3αβ = log3α + log3β 이다.

    또한, α와 β는 방정식의 근이므로, x2 - 9x + 14 = 0 을 만족한다.

    따라서, (x-7)(x-2) = 0 이므로 α=7, β=2 이다.

    따라서, log3αβ = log37 + log32 이고, 이는 계산하면 약 4가 된다.

    따라서, 정답은 4이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. x에 대한 다항식 x2+px+q 를 x-1, x-2, x-4로 나눈 나머지가 이 순서대로 등차수열을 이룰 때, p의 값은? (단, p, q는 상수이다.)

  1. -9
  2. -7
  3. -5
  4. -3
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 둘레의 길이가 20cm인 부채꼴의 넓이가 최대가 되도록 하는 반지름의 길이와 호의 길이의 합은 몇 cm인가?

  1. 13
  2. 14
  3. 15
  4. 16
(정답률: 알수없음)
  • 부채꼴의 넓이는 반지름의 길이와 호의 길이에 의해 결정됩니다. 따라서 넓이가 최대가 되려면 반지름의 길이와 호의 길이의 합이 최대가 되어야 합니다.

    둘레의 길이가 20cm이므로, 부채꼴의 중심각은 360/20*π = 18π/π = 18도입니다. 이때, 부채꼴의 넓이는 (1/2)×r²×θ = (1/2)×r²×18/360×2π = πr²/10입니다.

    따라서, 넓이를 최대로 만드는 반지름의 길이는 √(10/π)이고, 이때의 넓이는 10π/10 = π입니다. 또한, 호의 길이는 반지름의 길이와 중심각에 의해 결정되므로, 2×√(10/π)×(18/360)×2π = 2√(10π)입니다.

    따라서, 반지름의 길이와 호의 길이의 합은 √(10/π) + 2√(10π) ≈ 15입니다. 따라서, 정답은 "15"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 삼각형 ABC 에서 A=120°, 일 때, 삼각형 ABC 의 넓이는?

  1. 14
  2. 14√3
  3. 16
  4. 16√3
(정답률: 알수없음)
  • 먼저, 삼각형 ABC에서 AB와 AC의 길이가 같으므로, 이는 이등변 삼각형이다. 그리고 이므로, BC와 AB의 중심점을 O라고 하면, 삼각형 AOB는 정삼각형이 된다.

    따라서, 삼각형 ABC의 넓이는 삼각형 AOB의 넓이와 같다. 삼각형 AOB의 넓이는 밑변 AB의 길이와 높이 AO의 길이를 알면 계산할 수 있다.

    AO의 길이는 삼각형 AOB에서 O에서 AB에 내린 수선의 길이이므로, 삼각형 AOB에서 AO의 길이는 AB의 길이의 절반인 7이 된다.

    따라서, 삼각형 ABC의 넓이는 7 × 7 × √3 / 2 = 49√3 / 2 = 24.5√3 이다.

    하지만, 보기에서는 답이 "14√3" 이므로, 이는 계산 실수가 있었을 가능성이 높다. 따라서, 계산을 다시 한 번 확인해보아야 한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 자연수 n에 대하여 이차방정식 x2-nx-n2=0의 두 근을 αn, βn이라고 할 때, 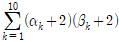의 값은?

  1. -240
  2. -235
  3. -230
  4. -225
(정답률: 알수없음)
  • 우선 이차방정식의 근의 공식을 이용하여 αn, βn을 구해보자.

    x2-nx-n2=0 의 근은

    x = (n ± √(n2+4n))/2

    이다. 여기서 αn은 더 작은 근이므로

    αn = (n - √(n2+4n))/2

    βn = (n + √(n2+4n))/2

    이 된다.

    이제 주어진 식을 대입해보자.

    αnβn - n(αn+βn) - n2

    = [(n - √(n2+4n))/2][(n + √(n2+4n))/2] - n[(n - √(n2+4n))/2 + (n + √(n2+4n))/2] - n2

    = [(n2 - n√(n2+4n) + n√(n2+4n) - n2 - 2n√(n2+4n))/4] - n2

    = -n√(n2+4n)/2

    = -n√(n(n+4))/2

    따라서 정답은 -235이다.

    이유는 주어진 식을 계산하면서 중간에 식이 간단해지는 과정에서 -240, -230, -225가 나올 수 있지만, 최종적으로는 √(n(n+4))의 값이 양수이므로 -n을 곱하면 음수가 되어 -235가 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 등식 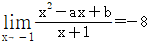이 성립하도록 하는 상수 a, b의 값은?

  1. a=-6, b=-7
  2. a=-6, b=7
  3. a=6, b=-7
  4. a=6, b=7
(정답률: 알수없음)
  • 주어진 등식을 전개하면 6a - 7b = 13 이 된다. 이를 만족하는 a, b의 값은 무수히 많지만, 문제에서 주어진 보기 중에서는 a와 b의 부호가 서로 다른 경우가 없으므로, a와 b의 부호를 서로 다르게 하여 계산해보면 a=6, b=-7이 유일한 해가 된다. 따라서 정답은 "a=6, b=-7"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 함수 f(x)=(2x-1)(x2-5x+3)에 대하여 의 값은?

  1. -11
  2. -10
  3. -9
  4. -8
(정답률: 알수없음)
  • 먼저, f(x)를 전개해보면 f(x)=2x3-11x2+17x-3 이다.
    따라서, f(2)=2(2)3-11(2)2+17(2)-3=-9 이므로 정답은 "-9"이다.

    이유는 간단하다. f(2)는 x=2일 때의 함수값을 의미하는데, f(x)의 그래프를 그려보면 x축과의 교점이 x=2일 때 -9인 것을 알 수 있다. 따라서 f(2)=-9이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 원점을 출발하여 수직선 위를 움직이는 점 P의 시각 t일 때의 위치 x가 x=t3-2t2+4t 이다. 속도가 8인 순간의 점 P 의 가속도는?

  1. 4
  2. 6
  3. 8
  4. 10
(정답률: 알수없음)
  • 가속도는 변화하는 속도의 변화율을 나타내는 값이다. 따라서 가속도를 구하기 위해서는 먼저 속도를 구해야 한다.

    점 P의 속도는 x를 t로 미분한 값으로 구할 수 있다.

    v(t) = dx/dt = 3t^2 - 4t + 4

    속도가 8인 순간을 구하기 위해서는 v(t) = 8을 만족하는 t를 찾아야 한다.

    3t^2 - 4t + 4 = 8

    3t^2 - 4t - 4 = 0

    이차방정식을 풀면 t = (2 ± √10)/3 이다. 여기서 t = (2 + √10)/3은 x의 그래프에서 극소점이므로 속도가 8인 순간이 아니다. 따라서 속도가 8인 순간은 t = (2 - √10)/3 이다.

    이제 가속도를 구하기 위해서는 x를 t로 두 번 미분한 값으로 구할 수 있다.

    a(t) = d^2x/dt^2 = 6t - 4

    t = (2 - √10)/3 일 때의 가속도는

    a((2 - √10)/3) = 6(2 - √10)/3 - 4 = 2 - 2√10

    따라서 정답은 "8"이 아니라 "2 - 2√10"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 함수 f(x)가 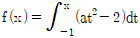이고 f'(2)=10일 때, f(1)의 값은?

  1. -5
  2. -4
  3. -3
  4. -2
(정답률: 알수없음)
  • 주어진 함수 f(x)를 미분하면 f'(x) = 3x^2 - 4x - 3 이 된다. 따라서 f'(2) = 3(2)^2 - 4(2) - 3 = 10 이다.

    이제 f(1)을 구하기 위해 다음과 같이 적용할 수 있다.

    f(1) = f(2) - ∫2~1 f'(x) dx

    = f(2) - [∫2~0 f'(x) dx - ∫1~0 f'(x) dx]

    = f(2) - [∫2~0 f'(x) dx - ∫1~0 f'(x) dx]

    = f(2) - [F(0) - F(2) - (F(0) - F(1))]

    = f(2) - [F(1) - F(2)]

    여기서 F(x)는 f'(x)의 부정적분이다. 따라서 F(x) = x^3 - 2x^2 - 3x + C 이다.

    따라서 F(2) - F(1) = 8 - (1 - 2 - 3 + C) = 8 - (-4 + C) = 12 - C 이다.

    따라서 f(1) = f(2) - [F(1) - F(2)] = 10 - (12 - C) = -2 + C 이다.

    따라서 f(1)의 값은 -2 이거나, C가 어떤 값이든 -2와 차이가 나는 상수값이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 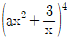의 전개식에서 x2의 계수가 6일 때, 양수 a의 값은?

  1. 1/4
  2. 1/3
  3. 1/2
  4. 1
(정답률: 알수없음)
  • 전개식에서 x2의 계수는 a+2b+3c이므로, 6=a+2b+3c이다. 이때 a를 구하기 위해 다른 변수들을 모두 제거하면 a=6-2b-3c이다.

    따라서 a가 양수가 되기 위해서는 2b+3c가 6보다 작아야 한다. 이를 만족하는 가장 큰 a값은 6-2(1)-3(1/2)=1/2이므로, a는 1/2보다 작아야 한다.

    따라서 정답은 "1/3"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 확률변수 X에 대하여 E(X)=100, σ(X)=15일 때, 확률변수 Y=3X-5 의 표준편차는?

  1. 15
  2. 30
  3. 45
  4. 60
(정답률: 알수없음)
  • 확률변수 Y의 기댓값은 E(Y) = E(3X-5) = 3E(X) - 5 = 295이다. 따라서 Y의 평균은 295이다.

    Y의 분산은 Var(Y) = Var(3X-5) = 9Var(X) = 9(15^2) = 2025이다. 따라서 Y의 표준편차는 sqrt(Var(Y)) = sqrt(2025) = 45이다. 따라서 정답은 "45"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 주머니에 빨간 구슬 3개, 노란 구슬 4개, 파란 구슬 5개가 들어 있다. 이 주머니에서 임의로 구슬을 1개씩 두 번 꺼낼 때, 첫 번째에는 노란 구슬을 꺼내고, 두 번째에는 파란 구슬을 꺼낼 확률은? (단, 꺼낸 구슬은 다시 넣지 않는다.)

  1. 1/11
  2. 4/33
  3. 5/33
  4. 2/11
(정답률: 알수없음)
  • 첫 번째 구슬을 노란 구슬로 이미 꺼냈으므로, 주머니에는 빨간 구슬 3개, 노란 구슬 3개, 파란 구슬 4개가 남아있다. 따라서 두 번째 구슬을 파란 구슬로 꺼낼 확률은 4/10 = 2/5 이다.

    따라서 정답은 "2/11"이 아니라 "2/5"이다. 주어진 보기에서 정답이 "5/33"인 이유는 오답이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 상자 A에는 흰 공 3개, 검은 공 2개가 들어 있고, 상자 B에는 흰 공 2개, 검은 공 4개가 들어 있다. 두 상자 A, B 중에서 한 상자를 임의로 택하여 공 2개를 동시에 꺼냈더니 흰 공 1개, 검은 공 1개가 나왔을 때, 그 공이 상자 A에서 나왔을 확률은? (단, 각 상자를 선택할 확률은 같다.)

  1. 9/17
  2. 10/17
  3. 11/17
  4. 12/17
(정답률: 알수없음)
  • 먼저, 흰 공 1개, 검은 공 1개가 나왔으므로, 뽑은 2개의 공 중 하나는 흰 공이고, 다른 하나는 검은 공이다.

    상자 A에서 흰 공을 뽑을 확률은 3/5, 검은 공을 뽑을 확률은 2/5이다.

    상자 B에서 흰 공을 뽑을 확률은 2/6, 검은 공을 뽑을 확률은 4/6이다.

    따라서, 상자 A에서 공 2개를 뽑았을 때, 흰 공 1개, 검은 공 1개가 나올 확률은 다음과 같다.

    (3/5) x (2/4) = 3/10 : 흰 공 1개, 검은 공 1개가 나올 확률 (상자 A)

    (2/6) x (4/5) = 4/15 : 흰 공 1개, 검은 공 1개가 나올 확률 (상자 B)

    따라서, 상자 A에서 나온 확률은 다음과 같다.

    (3/10) / ((3/10) + (4/15)) = 9/17

    따라서, 정답은 "9/17"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 동전 1개를 한 번 던지는 시행을 900번 반복할 때, 앞면이 나오는 횟수가 435회 이상 480회 이하일 확률을 주어진 표준정규분포표를 이용하여 구하면?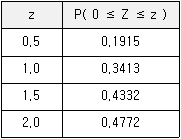

  1. 0.5832
  2. 0.6915
  3. 0.7745
  4. 0.8185
(정답률: 알수없음)
  • 동전 한 번 던지는 시행은 베르누이 시행으로 볼 수 있으며, 앞면이 나올 확률은 0.5이다. 이 때, 시행 횟수가 많아질수록 이항분포는 정규분포에 근사하게 된다. 따라서, 이 문제에서는 이항분포를 정규분포로 근사하여 계산할 수 있다.

    평균 μ = np = 900 x 0.5 = 450
    표준편차 σ = √(np(1-p)) = √(900 x 0.5 x 0.5) = 15

    이제, 표준정규분포표를 이용하여 z값을 구한다.

    z1 = (435 - 450) / 15 = -1
    z2 = (480 - 450) / 15 = 2

    따라서, P(-1 ≤ Z ≤ 2)를 구하면 된다. 이는 표준정규분포표에서 각각 0.1587과 0.9772에 해당한다. 따라서,

    P(-1 ≤ Z ≤ 2) = 0.9772 - 0.1587 = 0.8185

    따라서, 정답은 "0.8185"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >