1과목: 과목 구분 없음
1. 전체집합 U의 임의의 두 부분집합 A, B에 대하여 다음 중 항상 옳은 것은? (단, U는 유한집합이고, 임의의 집합 S에 대하여 n(S)는 S원소의 개수를, SC는 S의 여집합을 나타낸다)
- n(A∪B)=n(A)+n(B)
- n(A∪BC)=n(U)-n(B)
- n(A-B)=n(A)-n(B)
- n(AC∩BC)=n(U)-n(A∪B)
2. 다음 <보기>에 대한 설명으로 옳은 것은?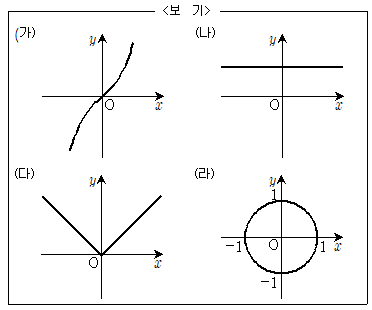
- 함수의 그래프는 4개이다.
- (나)는 항등함수이다.
- (다)는 상수함수이다.
- 일대일함수의 그래프는 1개이다.
3. 좌표평면상에서 그림과 같이 중심이 원점 O인 임의의 원을 10등분하여 각 분점을 차례로 P0, P1…, P9이라 하자. ∠P0OP1=θ라 할 때, sinθ+sin(2θ)+…+sin(10θ)의 값은?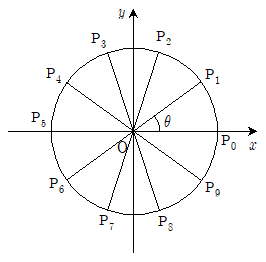
- 0
- π
- 2π
- 3π
4. x+y=2√5, xy=4, x>y일 때, x/y-y/x의 값은?
- √2
- √3
- 2
- √5
5. 임의의 두 실수 a, b에 대하여 연산 *을 a*b=a+b+4라고 정의할 때, 연산 *에 대한 2의 역원은?
- -10
- -4
- 4
- 10
6. 두 실수 x, y에 대하여 복소수 z-xy+(x+y)i가 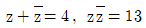 , 을 만족할 때, x2+y2의 값은? (단, i=√-1이고
, 을 만족할 때, x2+y2의 값은? (단, i=√-1이고 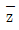 는 z의 켤레복소수이다.)
는 z의 켤레복소수이다.)
- 1
- 3
- 5
- 7
7. 좌표평면 위의 점 P가 원점 O 및 x축 위의 한 점 A(5, 0)에 대하여 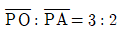 를 유지하며 움직인다. 이때, 점 P가 그리는 도형의 길이는?
를 유지하며 움직인다. 이때, 점 P가 그리는 도형의 길이는?
- 12π
- 14π
- 16π
- 18π
8. ∠B=π/3, 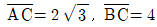 인 삼각형 ABC의 넓이는?
인 삼각형 ABC의 넓이는?
- 2√3
- 6
- 12
- 8√3
9. 함수 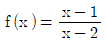 의 역함수가
의 역함수가 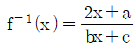 일 때, 상수 a, b, c의 합 a+b+c의 값은?
일 때, 상수 a, b, c의 합 a+b+c의 값은?
- -2
- -1
- 1
- 2
10. 삼각형 ABC의 세 변 AB, BC, CA의 길이를 각각 c, a, b라 하자. 세 변의 길이 a, b, c가 관계식 2b2=a2+c2을 만족할 때, 각 B의 최댓값은?
- π/6
- π/4
- π/3
- π/2
11. 상수 a, b에 대하여 행렬 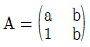 가
가 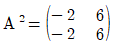 을 만족할 때, a-b의 값은?
을 만족할 때, a-b의 값은?
- 2
- 3
- 4
- 5
12. 두 함수 y=3, y=3x/9 의 그래프와 직선 y=3의 교점을 각각 P, Q라 할 때, 선분 PQ의 길이는?
- 1
- 2
- 3
- 4
13. 수열 {an}에 대하여 a1=2이고 an+1=2an-1일 때, a10의 값은?
- 512
- 513
- 1024
- 1025
14. 방사선 입자가 보호막을 한 개 통과할 때마다 방사선 입자의 양은 직전의 2/5가 된다고 하자. 이때, 방사선 입자의 양이 처음의 1/100이하가 되도록 하기 위해 필요한 최소한의 보호막의 개수는? (단, log2=0.310으로 계산한다)
- 6개
- 7개
- 8개
- 9개
15. 양수 a, b에 대하여 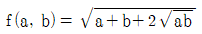 라 할 때,
라 할 때, 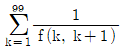 의 값은?
의 값은?
- 8
- 9
- 10
- 11
16. 다음 <보기> 중 x=1에서 연속인 함수만을 모두 고른 것은?
- ㄱ, ㄷ
- ㄴ, ㄹ
- ㄷ, ㄹ
- ㄱ, ㄴ, ㄹ
17. 미분 가능한 함수 f(x)에 대하여 다음의 함수 g(x)가 모든 실수 x에 대하여 연속일 때, f′(1)의 값은?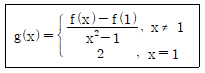
- 1
- 2
- 3
- 4
18. 구간 [0, d]에서 정의된 함수 y==f(x)의 그래프가 다음과 같을 때, 함수 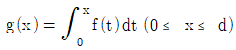 의 최댓값은? (단, 상수 a, b, c, d는 0 < a < b <c < d를 만족한다.)
의 최댓값은? (단, 상수 a, b, c, d는 0 < a < b <c < d를 만족한다.)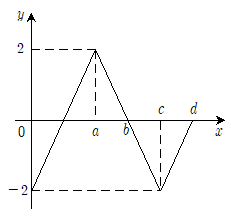
- g(a)
- g(b)
- g(c)
- g(d)
19. 연속확률변수 X의 확률밀도함수가 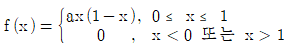 일 때, 확률
일 때, 확률 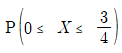 의 값은? (단, a는 양의 상수이다)
의 값은? (단, a는 양의 상수이다)
- 9/16
- 21/32
- 3/4
- 27/32
20. 영업팀 직원 2명, 재무팀 직원 3명, 인사팀 직원 4명으로 구성된 동호회 회원들을 일렬로 세울 때, 인사팀 직원끼리 서로 이웃하지 않을 확률은?
- 5/9
- 5/42
- 5/36
- 5/18






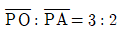 각도만큼 이동한 호이다. 이때 호의 길이는 원의 둘레의
각도만큼 이동한 호이다. 이때 호의 길이는 원의 둘레의
설명:
- "n(A∪B)=n(A)+n(B)" : 이는 합집합의 크기를 구하는 공식으로, A와 B의 원소들을 중복 없이 합친 집합의 크기는 A의 원소 개수와 B의 원소 개수를 더한 것과 같다는 것을 의미한다.
- "n(A∪BC)=n(U)-n(B)" : 이는 여집합을 이용한 공식으로, A와 B의 원소들을 중복 없이 합친 집합의 여집합은 A와 B의 여집합을 교집합한 것과 같다는 것을 의미한다. 따라서 A와 B의 여집합의 크기를 빼면 전체 집합 U에서 B의 원소 개수를 뺀 것과 같다.
- "n(A-B)=n(A)-n(B)" : 이는 차집합의 크기를 구하는 공식으로, A에서 B의 원소들을 뺀 집합의 크기는 A의 원소 개수에서 B의 원소 개수를 뺀 것과 같다는 것을 의미한다.
- "n(AC∩BC)=n(U)-n(A∪B)" : 이는 여집합과 교집합을 이용한 공식으로, A와 B의 여집합의 교집합의 크기는 A와 B의 원소들을 중복 없이 뺀 집합의 크기와 같다는 것을 의미한다. 따라서 전체 집합 U에서 A와 B의 원소들을 중복 없이 합친 집합의 크기를 빼면 A와 B의 여집합의 교집합의 크기와 같다.