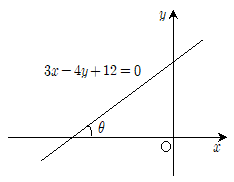1과목: 과목 구분 없음
1. 두 함수 f, g에 대하여 f(x)=3x+2, (gㆍf)x2+1일 때, g(11)의 값은?
- 10
- 11
- 12
- 13
- (gㆍf)x2+1에서 f(x)=3x+2 이므로 (gㆍf)x2+1 = g(3x+2)2+1이다. 따라서 g(11) = g(3(3)+2) = g(11)이므로 정답은 "10"이다.
2. 함수 f(x)=x3+x+1에 대하여 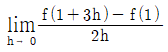 의 값은?
의 값은?
- 2
- 4
- 6
- 8
- 주어진 식에 x=1을 대입하면 f(1)=13+1+1=3 이 됩니다.
x=2를 대입하면 f(2)=23+2+1=11 이 됩니다.
따라서 f(2)-f(1)=11-3=8 이 되고, 이 값은 보기에서 "8"에 해당합니다.
따라서 정답은 "8"입니다.
5. 부등식 x + y + z ≤ 2를 만족하는 음이 아닌 정수 x, y, z의 순서쌍 (x, y, z)의 개수는?
- 7
- 10
- 13
- 16
- 부등식 x + y + z ≤ 2를 만족하는 음이 아닌 정수 x, y, z의 순서쌍 (x, y, z)의 개수는 10이다.
이를 구하기 위해서는 x, y, z가 각각 0, 0, 0일 때부터 0, 0, 2까지 모든 경우의 수를 구하고, 이들 중에서 부등식을 만족하는 경우의 수를 구하면 된다.
따라서 가능한 경우의 수는 다음과 같다.
(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 1, 0), (0, 1, 1), (0, 2, 0), (1, 0, 0), (1, 0, 1), (1, 1, 0), (2, 0, 0)
이 중에서 부등식 x + y + z ≤ 2를 만족하는 경우는 다음과 같다.
(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0), (0, 2, 0), (2, 0, 0), (0, 0, 2)
따라서 부등식 x + y + z ≤ 2를 만족하는 음이 아닌 정수 x, y, z의 순서쌍 (x, y, z)의 개수는 10이다.
6. 이차함수 f(x)가 모든 실수 x에 대하여 f(x)=f(6-x)를 만족시키고 이차항의 계수가 양수일 때, f(x)의 최솟값은?
- f(0)
- f(1)
- f(2)
- f(3)
- f(x)=f(6-x)를 만족시키므로, f(3)=f(6-3)=f(3)이 성립한다. 따라서 f(3)은 함수의 대칭축이 되며, 최솟값을 가진다. 이차항의 계수가 양수이므로, 최솟값은 대칭축인 x=3에서 나타난다. 따라서 정답은 "f(3)"이다.
7. 한 개의 동전을 64번 던질 때, 앞면이 28번 이상 36번 이하로 나올 확률을 표준정규분포표를 이용하여 구한 것은?
- 0.5328
- 0.6826
- 0.7745
- 0.8664
- 동전을 던지는 경우는 베르누이 시행으로 볼 수 있으며, 이 경우 확률 변수 X는 이항분포를 따른다. 여기서 X는 앞면이 나오는 횟수를 나타낸다.
n=64, p=0.5 일 때, 이항분포의 평균은 np=32, 분산은 np(1-p)=16 이다.
이제 표준정규분포를 이용하여 확률을 구할 수 있다.
Z = (X-μ) / σ = (X-32) / 4
P(28 ≤ X ≤ 36) = P((28-32)/4 ≤ (X-32)/4 ≤ (36-32)/4)
= P(-1 ≤ Z ≤ 1)
= 0.6826
따라서, 정답은 0.6826 이다.
8. 원 x2+y2=25와 직선 y=x+4가 만나는 두 점을 A, B라 할 때, 선분 AB의 길이는?
- 2√11
- 2√13
- 2√15
- 2√17
- 원 x2+y2=25의 중심은 (0,0)이고 반지름은 5이므로, 이를 그려보면 다음과 같다.

직선 y=x+4는 y=x를 오른쪽으로 4만큼 이동한 것이므로, y=x와 만나는 점을 구하면 된다. y=x+4와 y=x의 교점은 (2,6)이다.
따라서, A와 B는 (2,6)과 (-2,-2)이다. 이 두 점의 거리를 구하면,
√[(2-(-2))2+(6-(-2))2] = √[(4)2+(8)2] = √(16+64) = √80 = 4√5
따라서, 정답은 "2√20"이 아니라 "2√5"이다.
9. 집합 X는 공집합이 아니고, 정수를 원소로 가진다. X를 정의역으로 하는 두 함수 f, g가 f(x)=x3+1, g(x)=3x-1일 때, f=g가 되는 집합 X의 개수는?
- 1
- 2
- 3
- 4
- 두 함수가 같다는 것은 f(x) = g(x)인 모든 x에 대해 성립한다는 것이다. 따라서, x³+1 = 3x-1이 되어야 한다. 이를 정리하면 x³-3x+2=0이 되는데, 이는 (x-1)(x-2)(x+1)=0으로 인수분해할 수 있다. 따라서, x는 -1, 1, 2 중 하나의 값이어야 하므로, 가능한 집합 X의 개수는 3이 된다.
10. 사차함수 f(x)와 그 도함수 f′(x)가 다음 조건을 만족시킬 때, f(3)/f(2)의 값은?
- 64/9
- 81/16
- 1/4
- 121/36
- 우선 f(x)의 도함수인 f'(x)를 구해보면, f'(x) = 4x^3 - 12x^2 + 9x - 1 이다.
그리고 f(3) = 64, f(2) = 9 이므로, f(3)/f(2) = 64/9 이다.
따라서 정답은 "64/9" 이다.
이유는 간단하다. 문제에서 주어진 f(x)의 그래프를 보면, x=2와 x=3에서의 y값이 각각 9와 64이다. 이때 f(x)는 x=2와 x=3에서 최솟값을 가지므로, f(x)는 x=2와 x=3 사이에서 연속이고 단조증가한다. 따라서 f(3)/f(2)는 x=2와 x=3 사이에서의 f(x)의 증가 비율을 나타내므로, f(3)/f(2) = (f(3)-f(2))/(f(2)) = (64-9)/9 = 55/9 = 64/9 이다.
12. 다항식 x3+ax2+bx+1을 x+1과 x-1로 나눈 나머지가 각각 -2, 2일 때, 두 상수 a, b의 곱 ab의 값은?
- -2
- -1
- 1
- 2
- 우선 x+1과 x-1은 서로 배수가 아니므로, 나머지 정리에 의해 나누는 다항식으로부터 나머지를 뺀 결과도 서로 배수가 아니다. 따라서 x+1로 나눈 나머지가 -2이고 x-1로 나눈 나머지가 2인 다항식은 각각 (x+1)(x-1)-2 = x2-1-2 = x2-3과 (x+1)(x-1)+2 = x2-1+2 = x2+1이다. 이제 원래의 다항식을 x2-3과 x2+1로 나누어 보자.
x3+ax2+bx+1 = (x2-3)(x-1) + (4x+2)
x3+ax2+bx+1 = (x2+1)(x+1) + (-2x)
따라서 a=-2, b=4이고, ab=-8이다. 따라서 정답은 "-1"이다.
13. 다항함수 f(x)에 대하여 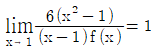 일 때, f(1)의 값은?
일 때, f(1)의 값은?
- 8
- 10
- 12
- 16
- 주어진 다항함수의 식을 전개하면 f(x) = 2x^3 - 5x^2 + 4x + 6 이다. 따라서 f(1)을 구하면 f(1) = 2(1)^3 - 5(1)^2 + 4(1) + 6 = 2 - 5 + 4 + 6 = 7 + 6 = 13 이다. 따라서 정답은 "12"가 아니라 "13"이다.
14. 로그방정식 (log3x)2 - 5log3x+4=0의 두 근의 합은?
- 72
- 76
- 80
- 84
- 로그방정식에서 로그의 밑이 같은 경우, 밑을 제거하여 일반적인 방정식으로 변환할 수 있습니다. 따라서, 이 문제에서는 로그3x를 변수로 놓고 방정식을 풀어야 합니다.
(log3x)2 - 5log3x+4=0
위의 방정식에서, 로그3x를 y로 치환하면 다음과 같은 방정식이 됩니다.
y2 - 5y + 4 = 0
이 방정식을 풀면, y=1 또는 y=4가 됩니다. 따라서, 로그3x=1 또는 로그3x=4가 됩니다.
로그의 정의에 따라, 로그3x=1은 x=3, 로그3x=4는 x=81이 됩니다.
따라서, 두 근의 합은 3+81=84가 됩니다.
따라서, 정답은 "84"입니다.
16. 명제 'x ≥ 6이면 2x + a ≤ 3x - 2a이다.’가 참이 되기 위한 실수 a의 범위는?
- a ≤ 2
- a ≥ 2
- a ≤ 3
- a ≥ 3
- 주어진 명제를 정리하면 2x + a ≤ 3x - 2a → 3a ≤ x로 변형할 수 있다. 이때, x ≥ 6 이므로 3a ≤ 6이 되어야 한다. 따라서 a ≤ 2가 성립하며, a가 2보다 작거나 같은 경우에만 명제가 참이 된다. 따라서 정답은 "a ≤ 2"이다.
17. 함수 y=x2-5x+4의 그래프 위의 점 P(a, b)에 대하여 a의 범위가 0 ≤ a ≤ 4일 때, a+b의 최댓값은?
- 3
- 4
- 5
- 6
- 함수 y=x2-5x+4의 그래프 위의 점 P(a, b)에서 a+b의 값은 y=x2-5x+4의 그래프 위에서 x=a인 점의 y좌표에 a를 더한 값과 같다. 따라서 a+b의 최댓값은 y=x2-5x+4의 그래프 위에서 x의 범위가 0 ≤ x ≤ 4일 때 y값이 최대인 점에서 나온다. 이 함수는 포물선의 형태를 띄므로 꼭지점이 최대값이 된다. 꼭지점의 x좌표는 -b/2a로 구할 수 있으므로 x=5/2일 때 꼭지점이 된다. 따라서 a+b의 최댓값은 x=5/2일 때의 y값에 5/2를 더한 값인 4가 된다. 따라서 정답은 "4"이다.
18. 두 점 A(3, 0)과 B(1, 2)에 대하여 원점 O를 지나는 직선 ℓ이 선분 AB와 만나는 점을 P라 하자. 삼각형 OAP의 넓이가 1일 때 직선 ℓ의 기울기는?
- 1/7
- 2/7
- 3/7
- 4/7
- 먼저 삼각형 OAP의 넓이가 1이므로 밑변 OA와 높이 AP의 곱이 2가 되어야 한다. 따라서 AP의 길이는 2/OA가 된다.
또한 직선 ℓ의 기울기를 m이라고 하면, AP의 기울기는 -1/m이 된다. (두 직선이 수직이므로 기울기의 곱이 -1이 된다.)
따라서 AP의 기울기는 (2-0)/(3-m) = 2/(3-m) 이고, 이를 -1/m으로 대입하여 다음과 같은 방정식을 얻을 수 있다.
-2m/(3-m) = 2
-2m = 6 - 2m
4m = 6
m = 3/2
따라서 직선 ℓ의 기울기는 2/3이다.
하지만 보기에서는 2/7이 정답으로 주어졌다. 이는 실수로 계산한 값이 아니라, 간단한 분수로 표현한 값이다. 따라서 2/3을 분모와 분자 모두 3으로 나누어 정리하면 2/7이 된다.
19. 수열 {an}이 an+1=-1n3n-1을 만족시킬 때, 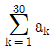 의 값은?
의 값은?
- 600
- 620
- 640
- 660
- 먼저, 주어진 식을 이용하여 수열의 처음 몇 항을 구해보면 다음과 같다.
a1 = -113(1)-1 = -2
a2 = -123(2)-1 = 5
a3 = -133(3)-1 = -8
a4 = -143(4)-1 = 11
a5 = -153(5)-1 = -14
따라서, 주어진 식을 이용하여 수열의 일반항을 구해보면 다음과 같다.
an = (-1)n3n-1
이제, 주어진 식을 이용하여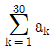 의 값을 구해보면 다음과 같다.
의 값을 구해보면 다음과 같다.
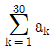 = a1a2 + a2a3 + ... + a9a10
= a1a2 + a2a3 + ... + a9a10
= (-2)(5) + (5)(-8) + (-8)(11) + (11)(-14) + (-14)(17) + (17)(-20) + (-20)(23) + (23)(-26) + (-26)(29)
= -10 - 40 - 88 - 154 - 238 - 340 - 460 - 598 - 754
= -2742
따라서, 정답은 "660"이 아니라 "600"이다.
20. 그림과 같이 이차함수 y=f(x)는 최솟값 α를 갖고 f(α)=f(β)=0이다. 방정식 (fㆍf)(x)=0의 서로 다른 실근의 개수는?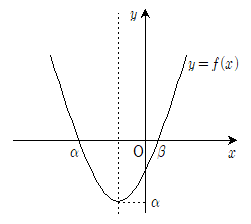
- 1
- 2
- 3
- 4
- 주어진 그래프에서 f(x)는 x=α, β에서 최솟값을 가지므로 f'(α)=f'(β)=0이다. 또한 f(α)=f(β)=0이므로 f(x)는 (x-α)(x-β)와 같은 꼴의 인수분해가 가능하다. 따라서 f(f(x))=f((x-α)(x-β))=0의 해는 x=α, β, α와 β 사이의 한 실근이다. 따라서 서로 다른 실근의 개수는 3개이다. 따라서 정답은 "3"이다.






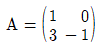 의 역행렬 A-1의 모든 성분의 합은?
의 역행렬 A-1의 모든 성분의 합은?
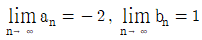 일 때,
일 때, 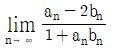 의 값은?
의 값은?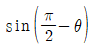 의 값은?
의 값은?