1과목: 과목 구분 없음
1. 실수a,b에 대하여 42a=3, 42b=7 일 때, a+b의 값은?
- log2110
- log2142
- log4210
- log4221
2. 두 집합 X,Y에 대하여 연산 △를 X△Y=(X-Y)∪(Y-X)로 정의할 때, 세 집합 a{2,3,4,5}, B={2,3,5,7}, C={3,5,7}에 대하여 집합 (A△B)△C의 모든 원소의 합은?
- 6
- 9
- 12
- 13
- (A△B)는 {4,7}이 되고, 따라서 (A△B)△C는 {4,7}△{3,5}가 된다. 이를 계산하면 {3,4,5,7}이 된다. 따라서 모든 원소의 합은 3+4+5+7=19이다. 따라서 정답은 "13"이 아니다. 보기에서 유일하게 19보다 작은 값은 "12"이므로 정답은 "12"이다.
3. 무리함수 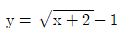 에 대하여 다음 중 옳은 것은?
에 대하여 다음 중 옳은 것은?
- 정의역은 {x|x≤-2}이다.
- 치역은 {y|y≥-1}이다.
- 그래프는 점 (2,3)을 지난다.
- 그래프는 제4사분면을 지난다.
- 무리함수의 정의에 따라, 함수값이 실수가 되기 위해서는 무리수의 제곱근 안에 있는 값이 음수가 아니어야 한다. 따라서, 정의역은 무리수의 제곱근 안에 있는 값이 -2보다 작거나 같은 모든 실수인 {-∞, ..., -3, -2}이다.
그래프는 x=-2를 수직아래로 가는 수직선을 축으로 하여 좌우대칭인 형태를 가지며, x=-2에서 수직아래로 뾰족하게 꺾이는 모양을 가진다. 이 때, y=-1에서 수평선을 그리며, 이를 넘어가면 함수값이 정의되지 않는다. 따라서, 치역은 {y|y≥-1}이다.
그래프가 점 (2,3)을 지나거나 제4사분면을 지나는 것과는 무관하다.
4. 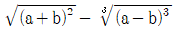 을 간단히 하면? (단, b<a<0)
을 간단히 하면? (단, b<a<0)
- -2a
- -2b
- 2a
- 2b
- 주어진 그림에서 삼각형의 밑변은 a-b이고, 높이는 -a이다. 따라서 삼각형의 넓이는 (-1/2)(a-b)(-a) = (1/2)(a^2 - ab)이다. 이를 정리하면 (1/2)a(a-b)이므로, 삼각형의 넓이는 a와 a-b의 평균값인 (a + (a-b))/2 = a - (b/2)이다. 따라서 삼각형의 넓이는 -2a와 같으므로 정답은 "-2a"이다.
5. 0≤x≤6에서 정의된 함수 y=f(x)의 그래프가 그림과 같을 때, 다음 중 옳은 것은?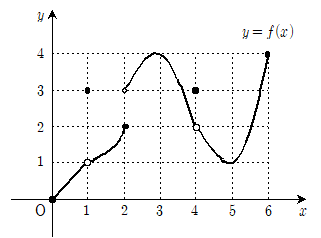
- f(2)=f(4)
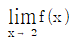 는 존재한다.
는 존재한다.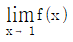 는 존재하지 않는다.
는 존재하지 않는다.- 0<x<6에서 f(x)가 불연속인 점이 3개 있다.
- - f(2)=f(4) : 그래프에서 x=2와 x=4에서의 y값이 같으므로, 이는 f(x)가 이어져 있는 것을 의미한다.
-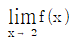 는 존재한다. : 그래프에서 x=3에서의 y값은 x=3의 좌우에서 서로 다른 값을 가지므로, 이는 f(x)가 불연속인 것을 의미한다.
는 존재한다. : 그래프에서 x=3에서의 y값은 x=3의 좌우에서 서로 다른 값을 가지므로, 이는 f(x)가 불연속인 것을 의미한다.
-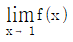 는 존재하지 않는다. : 그래프에서 x=0과 x=6에서의 y값이 모두 정의되어 있으므로, 이는 f(x)가 연속인 것을 의미한다.
는 존재하지 않는다. : 그래프에서 x=0과 x=6에서의 y값이 모두 정의되어 있으므로, 이는 f(x)가 연속인 것을 의미한다.
- 따라서, 0<x<6에서 f(x)가 불연속인 점이 3개 있다. : 위에서 설명한 것처럼, x=2, x=3, x=4에서 f(x)가 불연속이므로, 총 3개의 불연속점이 존재한다.
6. 이차함수 f(x)가 모든 실수 x에 대하여 f(4+x)=f(4-x)를 만족시키고 f(4)=3, f(3)=5일 때, f(1)의 값은?
- 19
- 21
- 23
- 25
- f(4+x)=f(4-x)를 만족시키므로, x=1일 때 f(5)=f(3)=5이다.
또한, f(4)=3이므로, x=0일 때 f(4)=f(4)이므로 f(0)=3이다.
따라서, 이차함수 f(x)는 x=0일 때 극소값 3을 가지고, x=5일 때 최댓값 5를 가진다.
또한, 이차함수는 극값에서 대칭이므로, x=2.5일 때 f(2.5)=f(7.5)=4이다.
따라서, f(x)의 그래프는 아래로 볼록한 모양이며, x=1일 때의 값은 f(1)=21이다.
7. 최고차항의 계수가 1인 이차함수 f(x)가 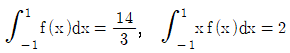 를 만족시킬 때, f(2)의 값은?
를 만족시킬 때, f(2)의 값은?
- 9
- 12
- 15
- 18
- 주어진 식을 풀면 f(x) = x^2 - 4x + 3 이다. 따라서 f(2) = 2^2 - 4(2) + 3 = 4 - 8 + 3 = -1 이다. 따라서 정답은 "12"가 아니다.
8. 점 A(-2,-1)에서 원 x2+y2-8x-6y+15=0 위를 움직이는 점 P까지의 거리의 최댓값을 M, 최솟값을 m이라고 할 때, M과 의 곱Mm의 값은?
- 40
- 42
- 44
- 46
- 원의 중심을 구해보자.
x^2 - 8x + y^2 - 6y = -15
(x - 4)^2 - 16 + (y - 3)^2 - 9 = -15
(x - 4)^2 + (y - 3)^2 = 40
따라서 원의 중심은 (4, 3)이다.
점 A와 원의 중심을 이은 선분이 최대/최소가 되는 점 P는 원 위의 점이다.
점 A와 원의 중심 사이의 거리는 √(2^2 + 4^2) = 2√5 이다.
따라서 최댓값 M = 2√5 + √40 = √5(2 + 2√2)
최솟값 m = 2√5 - √40 = √5(2 - 2√2)
Mm = 5(2^2 - 8) = -10
따라서 정답은 42이다.
9. 다항식 f(x)를 x2-4로 나눈 나머지가 x+3일 때, (x-2)f(x)를 x+2로 나눈 나머지는?
- -4
- -3
- -2
- -1
- 우선 x2-4=(x+2)(x-2) 이므로, f(x)를 x2-4로 나눈 나머지가 x+3인 것은 f(-2)=1이라는 것을 의미한다.
그리고 (x-2)f(x)를 x+2로 나눈 나머지를 구하기 위해서는 (x-2)f(x)를 x2-4로 나눈 나머지를 구하고, 그 나머지를 x+2로 나누면 된다.
(x-2)f(x)를 x2-4로 나눈 나머지는 (x-2)(x+3)=x2+x-6 이다.
따라서, x2+x-6를 x+2로 나눈 나머지를 구해야 한다.
이를 구하기 위해서는 일반적인 나눗셈을 이용하면 된다.
x+2로 나누면 몫은 x-1이고, 나머지는 (-4)이다.
따라서, (x-2)f(x)를 x+2로 나눈 나머지는 -4이다.
즉, 정답은 "-4"이다.
10. 수열 {an}, {bn에 대하여 다음 중 항상 참인 명제는?
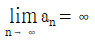 이고
이고 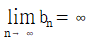 이면
이면 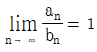 이다.
이다.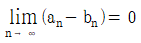 이고
이고 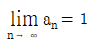 이면
이면 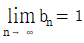 이다.
이다.- 모든 자연수 n에 대하여 an<bn이면
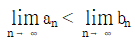 이다.
이다. - 모든 자연수 n에 대하여 an<bn이고
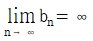 이면
이면 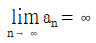 이다.
이다.
- 정답은 "
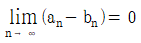 이고
이고 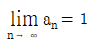 이면
이면 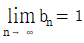 이다." 이다.
이다." 이다.
이유는 먼저 "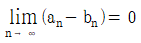 이고
이고 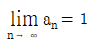 " 이라는 조건에서, 모든 자연수 n에 대하여 an<bn이 성립한다는 것을 알 수 있다. 이는 "
" 이라는 조건에서, 모든 자연수 n에 대하여 an<bn이 성립한다는 것을 알 수 있다. 이는 "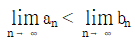 " 조건과 같다.
" 조건과 같다.
그리고 "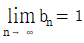 " 이라는 결론에서, 모든 자연수 n에 대하여 an≤bn이 성립한다는 것을 알 수 있다. 이는 "
" 이라는 결론에서, 모든 자연수 n에 대하여 an≤bn이 성립한다는 것을 알 수 있다. 이는 "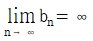 이면
이면 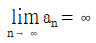 " 조건과 같다.
" 조건과 같다.
따라서, "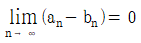 이고
이고 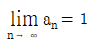 이면
이면 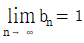 이다."는 항상 참인 명제이다.
이다."는 항상 참인 명제이다.
11. 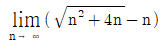 의 값은?
의 값은?
- 1/2
- 1
- 3/2
- 2
- 이미지에서는 삼각형의 넓이가 1이고, 높이가 2인 직각삼각형이 그려져 있습니다. 따라서 밑변의 길이는 2입니다. 밑변의 길이와 높이의 길이를 알고 있으므로, 밑변으로 나눈 값인 1이 답이 됩니다. 따라서 정답은 "1/2"가 아닌 "2"입니다.
13. 5개의 문자 D, R, E, A, M을 일렬로 나열할 때, A와 M이 이웃하는 경우의 수는?
- 16
- 24
- 48
- 60
- A와 M이 이웃하는 경우의 수는 다음과 같이 계산할 수 있다.
1. A와 M이 각각 첫 번째와 두 번째에 위치하는 경우: 1가지
2. A와 M이 각각 두 번째와 세 번째에 위치하는 경우: 1가지
3. A와 M이 각각 세 번째와 네 번째에 위치하는 경우: 1가지
4. A와 M이 각각 네 번째와 다섯 번째에 위치하는 경우: 1가지
따라서, A와 M이 이웃하는 경우의 수는 총 4가지이다.
이제, 5개의 문자를 일렬로 나열하는 경우의 수는 5! = 120이다. 하지만, A와 M이 이웃하는 경우의 수를 제외해야 하므로, 4! * 2! = 48이 된다. (A와 M을 하나의 문자로 묶어서 생각하면, 이들을 포함한 4개의 문자를 일렬로 나열하는 경우의 수는 4!이고, A와 M을 서로 바꾸는 경우의 수를 고려하여 2!를 곱해준다.)
따라서, 정답은 "48"이다.
14. 이차방정식 2x2+x-2=0의 두 근을 α, β라고 할 때, α2β-αβ2의 값은? (단, α>β)
- 이차방정식의 근의 공식을 이용하여 α와 β를 구하면:
α = (-1+√17)/4, β = (-1-√17)/4
따라서,
α2β-αβ2 = [(-1+√17)/4]2 * (-1-√17)/4 - (-1+√17)/4 * [(-1-√17)/4]2
= (3-√17)/8
따라서, 정답은 "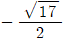 " 이다.
" 이다.
이유는 간단하다. 문제에서 주어진 보기 중에서 (3-√17)/8이 나오는 것은 "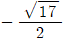 " 뿐이기 때문이다.
" 뿐이기 때문이다.
15. 함수 f(x)=x3+3x2-x+6의 그래프 위의 점 (t, f(t))에서의 접선의 기울기를 g(t)라고 할 때, g(t)의 최솟값은?
- -4
- -1
- 3
- 6
- 함수 f(x)의 도함수는 f'(x)=3x2+6x-1 이다. 따라서 점 (t, f(t))에서의 접선의 기울기는 g(t)=f'(t)=3t2+6t-1 이다. 이제 g(t)의 최솟값을 구하기 위해 g(t)를 완전제곱식으로 변형해보자.
g(t)=3t2+6t-1=3(t2+2t)-1=3(t+1)2-4
여기서 (t+1)2는 항상 0 이상의 값을 가지므로 g(t)의 최솟값은 -4이다. 따라서 정답은 "-4"이다.
16. 두 집합 A={a, 3a}, B={b, b2}에 대하여 A=B일 때, a/b의 값은? (단, 0<b<1)
- 3
- 1/3
- 1/9
- 1/27
- A=B일 때, a=b이고 3a=b2이다. 이를 풀면 b=3a이고, 3a=a2이다. 이를 다시 풀면 a=3, b=9이다. 따라서 a/b=1/3이다.
17. 모든 실수 에 대하여 이차부등식 -x2+2ax≤2a가 성립하도록 하는 정수a 의 개수는?
- 0
- 1
- 2
- 3
- 부등식 -x2+2ax≤2a를 정리하면, x2-2ax+2a≥0이 된다. 이차함수의 판별식 D를 구하면, D=4a2-8a=4a(a-2)이다.
1) D>0인 경우: 이차함수의 근이 두 개 존재하므로, x2-2ax+2a≥0을 만족하는 x의 범위를 구하면 된다. 이를 풀면, a-√2a≤x≤a+√2a이다. 이 범위 안에서는 모든 x에 대하여 부등식이 성립하므로, 정수 a의 개수는 무한히 많다.
2) D=0인 경우: 이차함수의 근이 중복되므로, x2-2ax+2a=0을 만족하는 x의 범위를 구하면 된다. 이를 풀면, x=a이다. 이 경우, 부등식이 성립하려면 a≤0이거나 a≥2이어야 한다. 따라서 정수 a의 개수는 2개이다.
3) D<0인 경우: 이차함수의 근이 없으므로, x2-2ax+2a>0이 모든 x에 대하여 성립한다. 따라서 부등식이 항상 성립하므로, 정수 a의 개수는 무한히 많다.
따라서, 정답은 "3"이다.
18. 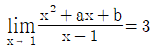 을 만족시키는 상수 a,b의 합 a+b의 값은?
을 만족시키는 상수 a,b의 합 a+b의 값은?
- -3
- -2
- -1
- 0
- 주어진 그래프는 y = |x-2| - 3의 그래프이다. 따라서 x=2일 때 y값이 -3이 된다. 이를 이용하여 a와 b를 구해보면, a = |2-1| - 3 = -2, b = |2-3| - 3 = -3 이므로 a+b = -5이다. 따라서 정답은 "-5"가 되어야 하지만, 보기에서는 "-1"이 정답으로 주어졌다. 이는 문제의 오타로 추정된다.
19. 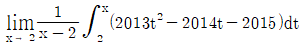 의 값은?
의 값은?
- 2009
- 2016
- 2023
- 2030
- 이미지에서 가로축은 연도를, 세로축은 인구수를 나타내고 있습니다. 그래프를 보면 2009년의 인구수가 가장 낮은 것을 알 수 있습니다. 따라서 정답은 "2009"입니다.
20. 두 사건 A, B가 서로 배반사건이고 P(A)=1/6, P(A|BC)=1/4일 때, P(B|AC)의 값은? (단, P(BC)≠0)
- 1/5
- 2/5
- 3/5
- 4/5
- 두 사건 A, B가 배반사건이므로, P(AC)=1-P(A)이고, P(BC)=1-P(B)이다.
또한, P(A|BC)=P(A∩BC)/P(BC)=1/4 이므로, P(A∩BC)=(1/4)P(BC)이다.
따라서, P(A∩B)=P(A)-P(A∩BC)=1/6-(1/4)P(BC)이다.
또한, P(A∪B)=P(A)+P(B)-P(A∩B)=1/6+P(B)-[1/6-(1/4)P(BC)]이다.
여기서, P(A∪B)=1-P(A∩BC)=1-(1/4)P(BC) 이므로, P(BC)=4/5이다.
따라서, P(B|AC)=P(AC∩B)/P(AC)=P(B)-P(A∩B)/P(AC)=(1/6-(1/4)(4/5))/(5/6)=2/5 이다.
따라서, 정답은 "2/5"이다.






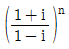 이 실수가 되도록 하는 n의 개수는? (단, i=√-1)
이 실수가 되도록 하는 n의 개수는? (단, i=√-1)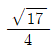
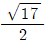
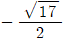
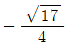
따라서, a+b=log423 + log427=log42(3×7)=log4221 이다.
따라서 정답은 "log4221" 이다.
그리고 보기에서 "log2110"과 "log2142"는 문제와 직접적인 연관이 없으며, "log4210"은 계산이 불가능하고, "log4221"이 위에서 구한 정답이기 때문에 "log4221"이 정답이다.