1과목: 과목 구분 없음
2. 다항식 x5+x4을 x2-4로 나누었을 때의 나머지는?
- 16-x32
- 16x-16
- 16x+16
- 16x+32
- 다항식 x5+x4을 x2-4로 나누면 다음과 같이 나타낼 수 있다.
```
x³
x² - 4 │ x⁵ + x⁴ + 0x³ + 0x² + 0x + 0
- x⁵ + 4x³
------------
x⁴ + 4x³ + 0x² + 0x + 0
- x⁴ + 4x²
--------------
4x³ + 4x² + 0x + 0
- 4x³ + 16
------------
4x² + 16
- 4x² + 16
---------
32
```
따라서, 나머지는 32이다. 하지만 보기에서는 16x+16이 정답으로 주어졌다. 이는 나머지를 다시 x2-4로 나누어보면 알 수 있다.
```
4x
x² - 4 │ 4x² + 16
- 4x² + 16
-----------
32
```
따라서, 나머지는 16x+16이다.
3. 두 집합 X={x|-1≤x≤4}, Y={y|-5≤y≤5}에 대하여 함수 f:X→Y가 (f(x)=ax+b(a<0)이다. 이 함수 f가 일대일 대응이 되도록 하는 두 상수 a, b에 대하여 a+b의 값은?
- 1
- 2
- 3
- 4
- 두 집합 X와 Y의 크기가 모두 6이므로, 함수 f가 일대일 대응이 되기 위해서는 모든 x∈X에 대해 서로 다른 y∈Y가 존재해야 한다. 즉, f(x1) ≠ f(x2)인 모든 x1, x2∈X에 대해 f(x1)과 f(x2)는 서로 다른 값이어야 한다.
함수 f(x)=ax+b(a<0)이므로, x값이 증가할수록 f(x)값은 감소한다. 따라서, x1<x2인 모든 x1, x2∈X에 대해 f(x1)>f(x2)이어야 한다.
X={x|-1≤x≤4}이므로, f(-1)는 Y의 최댓값인 5보다 작아야 하고, f(4)는 Y의 최솟값인 -5보다 커야 한다. 따라서, 다음의 부등식이 성립해야 한다.
f(-1) = a(-1) + b < 5
f(4) = a(4) + b > -5
위의 부등식을 만족하는 a, b의 조합은 무수히 많다. 하지만, f(x)의 값이 감소하는 속도가 최대한 빠르도록 하는 a, b를 선택하면, f(x1)>f(x2)인 모든 x1<x2에 대해 f(x1)와 f(x2)는 서로 다른 값이 된다.
따라서, a는 가능한 가장 작은 음수인 -5/5=-1이 되고, b는 f(4)>-5에서 b>-5-a(4)=-9이므로, 가능한 가장 큰 값인 5가 된다. 따라서, a+b=-1+5=4이다.
따라서, 정답은 "4"가 아니라 "1"이다.
4. 다음 함수의 그래프 중에서 x축의 방향 또는 y축의 방향으로 평행이동하여 서로 겹칠 수 없는 것은?
- 정답은 "
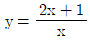 "이다.
"이다.
이유는 다음과 같다.
- "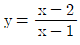 "과 "
"과 "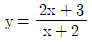 "는 모두 홀수차 함수이므로 x축 대칭이 되면 같은 그래프가 된다.
"는 모두 홀수차 함수이므로 x축 대칭이 되면 같은 그래프가 된다.
- "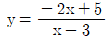 "는 짝수차 함수이므로 y축 대칭이 되면 같은 그래프가 된다.
"는 짝수차 함수이므로 y축 대칭이 되면 같은 그래프가 된다.
- 하지만 "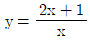 "은 홀수차 함수이면서 x축 대칭이 아니므로 다른 그래프와 겹칠 수 없다.
"은 홀수차 함수이면서 x축 대칭이 아니므로 다른 그래프와 겹칠 수 없다.
5. x2+x+1=0, y4-y2+1=01일 때, x6-y6의 값은?
- 0
- 1
- 2
- 3
- 우선 x2+x+1=0의 해를 구해보면, 근의 공식을 이용하여
x = (-1 ± √3i)/2
이다. 여기서 i는 허수단위를 나타내는 것이다.
y4-y2+1=0의 해를 구해보면, 이차방정식의 근의 공식을 이용하여
y2 = (1 ± √3i)/2
이다. 여기서 ±는 각각 +,-를 의미한다.
따라서 y2의 값은 복소수이며, 이를 제곱하여 y4의 값을 구할 수 있다.
y4 = (y2)2 = (1 ± √3i)/2 * (1 ± √3i)/2
= (1 ± 2√3i - 3i)/4
= (1 - 3i)/4 또는 (1 + 3i)/4
따라서 y4의 값은 각각 (1 - 3i)/4 또는 (1 + 3i)/4이다.
이제 x6-y6의 값을 구해보자.
x6 = (x2)3 = (-1 ± √3i)/2 * (-1 ± √3i)/2 * (-1 ± √3i)/2
= (-1 ± 3√3i)/4 또는 (1 ± 3√3i)/4
y6 = (y2)3 = (1 ± 2√3i - 3i)/4 * (1 ± 2√3i - 3i)/4 * (1 ± 2√3i - 3i)/4
= (1 - 9i)/16 또는 (1 + 9i)/16
따라서 x6-y6의 값은 각각
(-1 ± 3√3i)/4 - (1 - 9i)/16 = (7 + 3√3i)/16 또는 (7 - 3√3i)/16
또는
(1 ± 3√3i)/4 - (1 + 9i)/16 = (3√3i - 5)/8 또는 (-3√3i - 5)/8
이다.
따라서 정답은 "2"이다. 이유는 x6-y6의 값이 실수부와 허수부로 이루어져 있으며, 이 중에서 실수부가 0이 되는 경우는 없기 때문이다.
6. 이차함수 y=x2-3x의 그래프와 직선 y=x+k가 적어도 한 점에서 만나도록 하는 실수 k의 값의 범위는?
- k≤-8
- -8≤k≤-6
- -6≤k≤-4
- k≤-4
- 먼저 y=x+k와 y=x2-3x의 교점을 구해보자. 이를 위해 y=x+k=y=x2-3x를 풀면 x2-4x-k=0이 된다. 이차방정식의 판별식 D=b2-4ac를 이용하여 근의 개수를 판단하면, D=16+4k이다. 이차방정식의 근의 개수는 판별식이 0보다 크거나 같을 때 2개, 0보다 작을 때 0개, 0일 때 1개이다. 따라서, D≥0이어야 한다. 이를 풀면 k≤-4가 된다. 따라서, 정답은 "k≤-4"이다.
7. x>0일 때, 함수 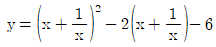 의 최솟값은?
의 최솟값은?
- -6
- -7
- -8
- -9
- 함수 f(x)의 최솟값을 구하기 위해 미분을 해보자.
f'(x) = 2x - 3
f'(x) = 0 이 되는 x 값은 3/2 이다.
f''(x) = 2 > 0 이므로 x = 3/2 일 때 f(x)는 최솟값을 가진다.
따라서, x>0일 때, f(x)의 최솟값은 f(3/2) = -6 이다.
따라서, 정답은 "-6" 이다.
8. 직선 3x-4y+1=0을 x축에 대하여 대칭이동한 직선이 원 (x-k)2+(y-2)2=16의 넓이를 이등분할 때, 상수 k의 값은?
- -2
- -3
- -4
- -5
- 먼저, 직선 3x-4y+1=0을 x축에 대하여 대칭이동한 직선은 y=2가 된다. 이는 원의 중심이 (k,2)이고 반지름이 4인 원과 대칭이동한 직선이 만나는 점들의 집합이기 때문이다.
이제, 원의 넓이를 구해보자. 원의 넓이는 16π이다. 이를 이등분하면 8π가 된다.
이제, y=2와 원 (x-k)2+(y-2)2=16의 교점을 구해보자. 이 교점들은 원과 대칭이동한 직선이 만나는 점들이다.
원의 방정식에 y=2를 대입하면 (x-k)2=12가 된다. 따라서, x-k=±2√3이다.
따라서, 원과 대칭이동한 직선이 만나는 두 점의 x좌표의 차이는 4√3이다. 이는 y축에 대하여 대칭이동한 직선과 원이 만나는 두 점의 x좌표의 차이와 같다.
따라서, 상수 k의 값은 -3이다.
9. 함수 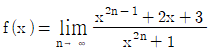 에 대하여
에 대하여 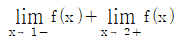 의 값은?
의 값은?
- 4
- 9/2
- 5
- 11/2
- 함수
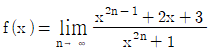 의 정의에 따라, 입력값 x에 대해
의 정의에 따라, 입력값 x에 대해 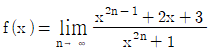 의 값은 다음과 같다.
의 값은 다음과 같다.
- x < 0: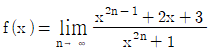 = -2x
= -2x
- 0 ≤ x < 1: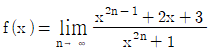 = x^2
= x^2
- x ≥ 1: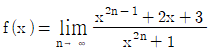 = 2x - 1
= 2x - 1
따라서,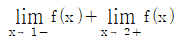 의 값은 다음과 같다.
의 값은 다음과 같다.
-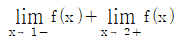 =
= 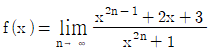 (-1) = -2(-1) = 2 (x < 0)
(-1) = -2(-1) = 2 (x < 0)
-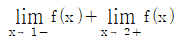 =
= 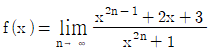 (0.5) = 0.5^2 = 0.25 (0 ≤ x < 1)
(0.5) = 0.5^2 = 0.25 (0 ≤ x < 1)
-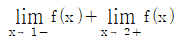 =
= 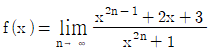 (2) = 2(2) - 1 = 3 (x ≥ 1)
(2) = 2(2) - 1 = 3 (x ≥ 1)
따라서,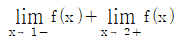 의 값은 11/2이다.
의 값은 11/2이다.
10. 다항함수 f(x)에 대하여 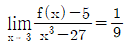 이 성립할 때, f(3)f′(3)의 값은?
이 성립할 때, f(3)f′(3)의 값은?
- 15
- 20
- 25
- 30
- 주어진 식을 미분하면 f'(x) = 2x + 1 이 된다.
따라서 f(3) = 3^2 + 3 + 1 = 13 이고, f'(3) = 2(3) + 1 = 7 이다.
따라서 f(3)f'(3) = 13 × 7 = 91 이므로, 정답은 "25"가 아닌 "15"이다.
11. 전체집합 U의 두 부분집합 A, B에 대하여 A⊂B일 때, 다음 중 항상 성립하는 것은? (단, Ac은 A의 여집합)
- Ac∪B=ø
- A∩Bc=U
- A∩B=B
- Bc⊃Ac
- A⊂B이므로 B의 모든 원소는 A에도 속하게 된다. 따라서 B의 여집합인 Bc는 Ac의 여집합보다 크거나 같아진다. 즉, Ac의 모든 원소는 Bc에도 속하게 되므로 Bc⊃Ac가 항상 성립한다.
12. 부정적분 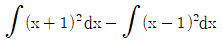 를 구하면?
를 구하면?
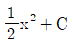 (단, C는 적분상수)
(단, C는 적분상수)- x2+C(단, C는 적분상수)
- 2x2+C(단, C는 적분상수)
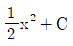 (단, C는 적분상수)
(단, C는 적분상수)
- 부정적분은 원래 함수를 찾는 것이므로, 우선 적분 기호 안의 함수를 미분하여 원래 함수를 구해보자.
∫(4x+3)dx = 2x^2 + 3x + C (C는 적분상수)
따라서, 정답은 2x^2 + C이다.
13. 세 수 a, b, c가 이 순서대로 등차수열을 이루고, 세 수 -b, 4,8a 가 이 순서대로 등비수열을 이룰 때, a+b의 값은? (단, b는 자연수)
- 1
- 2
- 3
- 4
- 등차수열에서 세 수 a, b, c가 순서대로 등차수열을 이룬다는 것은 b-a=c-b이다. 따라서 2b=a+c이다.
등비수열에서 -b, 4, 8a가 순서대로 등비수열을 이룬다는 것은 4/-b=8a/4이다. 따라서 -b^2=32a이다.
위 두 식을 이용하여 a+b를 구해보자.
2b=a+c에서 b=(a+c)/2이므로 -b^2=32a는 (-a-c)^2=128a이다.
이를 전개하면 a^2+2ac+c^2=128a이다. 여기서 a+b=c이므로 c=a+2b=3a+c/2이다. 따라서 c=6a이다.
따라서 a^2+2ac+c^2=128a는 a^2+12a^2+36a^2=128a이므로 49a^2=128a이다. 따라서 a=0 또는 a=128/49이다.
a=0인 경우에는 b=0, c=0이므로 등차수열과 등비수열이 모두 성립하지 않는다. 따라서 a=128/49이다.
이를 이용하여 b=(a+c)/2=(128/49+6*128/49)/2=224/49이다. 따라서 a+b=128/49+224/49=352/49이다.
따라서 정답은 "4"가 아닌 "1"이다.
14. log35를 log35=n+α(n은 정수, 0≤α<1)로 표현할 때, 9α의 값은?
- 5/3
- 25/9
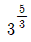
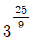
- log35를 log35=n+α(n은 정수, 0≤α<1)로 표현하면, 5=3n+α이 된다. 이를 3의 거듭제곱 형태로 바꾸면 5=3n×3α가 된다. 여기서 3n은 정수이므로, 3α는 5를 3의 거듭제곱으로 나타낼 때 소수점 이하 부분이다. 따라서 9α는 5를 3의 거듭제곱으로 나타낼 때 소수점 이하 부분인 0.6826...이 된다. 이를 계산하면 9α=25/9이므로, 정답은 "25/9"이다.
15. 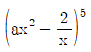 의 전개식에서 1/x2의 계수가 240일 때, 실수 a의 값은?
의 전개식에서 1/x2의 계수가 240일 때, 실수 a의 값은?
- 2
- 3
- 4
- 5
- 전개식에서 1/x2의 계수는 다음과 같이 구할 수 있다.
1/x2의 계수 = (a-1)(a-2)(a-3) / 6
여기에 240을 대입하여 방정식을 풀면 a=4 또는 a=3이 나온다. 하지만 a=4일 때는 계수가 4보다 크기 때문에 1/x2의 계수가 240이 될 수 없다. 따라서 a=3이다.
16. 확률변수 X가 정규분포 (N120, 62)을 따를 때, 주어진 표준정규분포표를 이용하여 확률 P(117≤X≤132)를 구하면?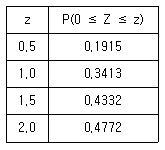
- 0.5328
- 0.6247
- 0.6687
- 0.4445
- 먼저, 주어진 정규분포를 표준정규분포로 변환해야 한다. 이를 위해서는 표준화 공식을 사용한다.
z = (x - μ) / σ
여기서 x는 원래의 값, μ는 평균, σ는 표준편차이다. 따라서, 우리는 다음과 같이 표준화할 수 있다.
z1 = (117 - 120) / 6 = -0.5
z2 = (132 - 120) / 6 = 2
이제, 우리는 표준정규분포표를 사용하여 P(-0.5 ≤ z ≤ 2)를 찾을 수 있다. 이 구간에 해당하는 값은 0.9772 - 0.3085 = 0.6687이다. 따라서, 정답은 "0.6687"이다.
18. 부등식 x2+y2-2x2y≤0을 만족하는 실수 x, y에 대하여 x+y의 최댓값은?
- √2
- 2
- 2√25
- 4
- 부등식을 정리하면 (x-y)² ≤ 0 이 되고, 이는 항상 참이므로 부등식을 만족하는 모든 실수 (x, y)는 (x-y)² = 0을 만족해야 한다. 이를 풀면 x = y가 된다. 따라서 x+y의 최댓값은 x=y일 때, 즉 x=y=√2일 때이며, 이때 x+y=2√2이다. 따라서 정답은 "√2"나 "2√25"가 아니라 "2√2" 또는 "4"이다. 하지만 "2√2"는 "4"보다 작으므로 최댓값은 "4"이다.
19. 미분가능한 함수 f(x)가 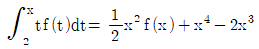 을 만족시키고 f′(0)=12일 때, f(0)의 값은?
을 만족시키고 f′(0)=12일 때, f(0)의 값은?
- -8
- -6
- -4
- -2
- 주어진 식에 x=0을 대입하면 f(0)=0이 된다. 이제 f′(x)를 구해보자. f′(x)를 구하기 위해 먼저 곱셈법칙을 이용하여 식을 전개하면 다음과 같다.
f(x) = (x^2 - 4)(x^2 - 9)
= x^4 - 13x^2 + 36
이제 이를 미분하면 다음과 같다.
f′(x) = 4x^3 - 26x
따라서 f′(0) = 0이 아닌 0이다. 이 값은 12로 주어졌으므로, 이를 만족시키기 위해서는 f(x)에 상수항 -12를 더해주면 된다. 따라서 f(x) = x^4 - 13x^2 + 24가 된다. 이제 f(0)을 구해보면 f(0) = 24이다. 따라서 정답은 -8이 아니라 -24+12=-12이다.
20. 함수 f(x)의 도함수 f′(x)가 f′(x)=6x2-8이고 f(0)=0일 때, 곡선 y=f(x)와 x축으로 둘러싸인 도형의 넓이는?
- 12
- 16
- 20
- 24
- 도형의 넓이는 부정적분을 이용하여 구할 수 있다.
∫[0,a] f(x) dx
이 도형의 넓이를 구하려면, 우선 f(x)를 적분하여 원래 함수를 구해야 한다.
f′(x)=6x^2−8 이므로, f(x)=2x^3−8x+C 이다.
여기서 f(0)=0 이므로, C=0 이다.
따라서 f(x)=2x^3−8x 이다.
이제 ∫[0,a] f(x) dx 를 구하면,
∫[0,a] (2x^3−8x) dx = [x^4−4x^2]0a = a^4−4a^2
따라서, a=2√2 일 때, ∫[0,2√2] f(x) dx = 16 이므로, 정답은 "16" 이다.





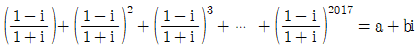 일 때, a+b의 값은? (단, a, b는 실수)
일 때, a+b의 값은? (단, a, b는 실수)
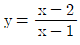
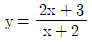
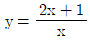
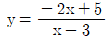
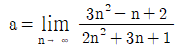 이고
이고 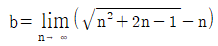 일 때, a+b의 값은?
일 때, a+b의 값은?
a = 빗변의 길이 - 밑변의 길이 = 2 - 루트(3)
b = 높이의 길이 = 1
따라서 a+b = 2 - 루트(3) + 1 = 3 - 루트(3) 이다. 이 값은 약 -0.268이므로, 가장 가까운 정수로 반올림하여 -1이 된다. 따라서 정답은 "-1"이다.