1과목: 과목 구분 없음
1. 집합 X={1,2,3,4,5,6}의 부분집합 중 2와 5는 원소로 가지고 3은 원소로 가지지 않는 부분집합의 개수는?
- 2
- 4
- 8
- 16
2. 이항분포 B(20,p)를 따르는 확률변수 X에 대하여 확률변수 2X+3의 평균이 13일 때, p의 값은?
- 1/2
- 1/3
- 1/4
- 1/5
- 확률변수 2X+3의 평균은 E(2X+3) = 2E(X) + 3 이다. 이항분포 B(20,p)의 평균은 E(X) = np 이므로, 2E(X) + 3 = 2np + 3 이다. 따라서, 2np + 3 = 7/2 이고, 이를 정리하면 p = 1/4 이다. 따라서, 정답은 "1/4" 이다.
3. 모든 자연수 n에 대하여 수열 {an}이 부등식 6n<(3n+1)an<6n+5를 만족시킬 때, 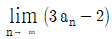 의 값은?
의 값은?
- 4
- 14/3
- 16/3
- 6
- 부등식을 정리하면 2<an<2+5/(3n+1)이다. 이를 만족하는 가장 작은 자연수 an은 3n+2이다. 따라서 a1=5, a2=8, a3=11, ... 이다. 이 수열의 일반항은 an=3n+2이므로,
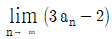 =3/2+4/5+5/8+...=∑n=1∞(n+2)/(3n+2)이다. 이 식을 분수 분해하면 ∑n=1∞(1/3-1/(3n+2))이다. 이 식은 텔레스의 파리도로 수열을 이용하여 쉽게 계산할 수 있다. 따라서
=3/2+4/5+5/8+...=∑n=1∞(n+2)/(3n+2)이다. 이 식을 분수 분해하면 ∑n=1∞(1/3-1/(3n+2))이다. 이 식은 텔레스의 파리도로 수열을 이용하여 쉽게 계산할 수 있다. 따라서 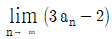 =1/3+1/6+1/9+...=∑n=1∞1/(3n)=1/3×∑n=1∞1/n=1/3×ln2=ln√2=0.3466... 이므로, 가장 가까운 정수로 반올림하여 정답은 "4"이다.
=1/3+1/6+1/9+...=∑n=1∞1/(3n)=1/3×∑n=1∞1/n=1/3×ln2=ln√2=0.3466... 이므로, 가장 가까운 정수로 반올림하여 정답은 "4"이다.
4. 계수가 유리수인 이차방정식 x2의 ax+b=0 한 근이 -1+√2일 때, 3a+2b의 값은?
- 1
- 2
- 3
- 4
- 주어진 이차방정식의 한 근이 -1+√2 이므로 다른 근은 -1-√2 이다. 이를 이용하여 방정식을 전개하면 다음과 같다.
(x-(-1+√2))(x-(-1-√2)) = 0
(x+1-√2)(x+1+√2) = 0
x2 + 2x - 1 = 0
따라서 a=1, b=-1 이다. 이를 이용하여 3a+2b를 계산하면 다음과 같다.
3a+2b = 3(1) + 2(-1) = 3-2 = 1
따라서 정답은 "1"이다.
5. 양의 실수 x에 대하여 logx의 정수 부분을 f(x), 소수 부분을 g(x)라 할 때, f(a)=f(99), g(a)=g(1200)을 만족시키는 a의 양의 약수의 개수는?
- 5
- 6
- 7
- 8
- 우선, logx의 정수 부분을 f(x)로 표현하면 다음과 같습니다.
f(x) = ⌊logx⌋
여기서 ⌊⌋는 소수점 이하를 버리는 함수입니다.
또한, logx의 소수 부분을 g(x)로 표현하면 다음과 같습니다.
g(x) = logx - ⌊logx⌋
이제 f(a) = f(99)와 g(a) = g(1200)를 이용하여 a를 구해보겠습니다.
우선 f(a) = f(99)이므로 다음과 같은 식이 성립합니다.
⌊loga⌋ = ⌊log99⌋
두 변에 exp를 취하면 다음과 같습니다.
ea > 99 > e(a-1)
여기서 e는 자연상수로 약 2.71828입니다.
따라서 a는 4보다 크고 5보다 작습니다.
이제 g(a) = g(1200)를 이용하여 a를 구해보겠습니다.
g(a) = loga - ⌊loga⌋
g(1200) = log1200 - ⌊log1200⌋ = 2.07918 - 3 = -0.92082
따라서 g(a) = -0.92082입니다.
이제 a의 양의 약수를 구해보겠습니다.
a는 4보다 크고 5보다 작으므로 a는 1, 2, 3, 4 중 하나입니다.
또한, g(a) = -0.92082이므로 다음과 같은 식이 성립합니다.
0.07918 < loga < 0.92082
따라서 a는 1보다 크고 10보다 작습니다.
따라서 a는 2 또는 3입니다.
따라서 a의 양의 약수는 1, 2, 3, 6입니다.
따라서 정답은 4개인 "6"입니다.
7. 다항식 f(x)를 3x2+5x-2로 나눈 나머지가 2x+5일 때, 다항식 f(6x-5)를 2x-1로 나눈 나머지는?
- 1
- 2
- 3
- 4
- 우선, 다항식 f(x)를 3x2+5x-2로 나눈 나머지가 2x+5이므로, 다음과 같은 식이 성립합니다.
f(x) = (3x2+5x-2)q(x) + (2x+5)
여기서 q(x)는 몫을 나타내는 다항식입니다.
이제, 다항식 f(6x-5)를 2x-1로 나눈 나머지를 구해야 합니다. 이를 구하기 위해서는 다음과 같은 과정을 거칩니다.
1. f(x)를 3x2+5x-2로 나눈 나머지를 구합니다.
2. f(x) 대신에 f(6x-5)를 넣어서 나머지를 구합니다.
3. 나머지 정리를 이용하여, f(6x-5)를 2x-1로 나눈 나머지를 구합니다.
따라서, 우선 f(x)를 3x2+5x-2로 나눈 나머지를 구해야 합니다.
f(x) = (3x2+5x-2)q(x) + (2x+5)
여기서 x를 6x-5로 대입하면,
f(6x-5) = (3(6x-5)2+5(6x-5)-2)q(6x-5) + (2(6x-5)+5)
= (3(36x2-60x+25)+30x-15-2)q(6x-5) + (12x-5)
= (108x2-165x+68)q(6x-5) + (12x-5)
이제, f(6x-5)를 2x-1로 나눈 나머지를 구하기 위해 나머지 정리를 이용합니다.
f(6x-5) = (2x-1)q'(x) + r
여기서 q'(x)는 몫을 나타내는 다항식이고, r은 나머지를 나타내는 다항식입니다.
위 식에서 양변에 x=3/2를 대입하면,
f(6(3/2)-5) = (2(3/2)-1)q'(3/2) + r
f(4) = 2q'(3/2) + r
따라서, f(6x-5)를 2x-1로 나눈 나머지는 2q'(3/2) + r입니다.
이제, 정답이 "1"인 이유를 설명하겠습니다.
위에서 구한 f(6x-5)를 2x-1로 나눈 나머지는 2q'(3/2) + r입니다. 이때, r은 나머지를 나타내는 다항식입니다.
하지만, r은 f(x)를 3x2+5x-2로 나눈 나머지가 2x+5인 다항식을 2x-1로 나눈 나머지와 같습니다.
즉, r은 2x+5를 2x-1로 나눈 나머지와 같습니다.
2x+5를 2x-1로 나눈 나머지는 1이므로, r은 1입니다.
따라서, f(6x-5)를 2x-1로 나눈 나머지는 2q'(3/2) + 1입니다.
따라서, 정답은 "1"입니다.
8. 모든 실수에서 연속인 함수 f(x)가 (x-2)f(x)=2x2-x+k를 만족시킬 때, k+f(2)의 값은? (단, k는 상수)
- -3
- -1
- 1
- 3
- 먼저 x=2를 대입하면 (2-2)f(2)=2(2)^2-2+k 이므로 k+f(2)=6입니다.
이제 (x-2)f(x)=2x^2-x+k 식 양변을 x로 미분하면 f(x)+(x-2)f'(x)=4x-1입니다.
여기서 f(x)는 연속이므로 f'(x)도 연속이며, 따라서 x=2에서도 f'(2)가 존재합니다.
따라서 x=2를 대입하면 f(2)+(2-2)f'(2)=4(2)-1 이므로 f'(2)=7/2입니다.
이제 (x-2)f(x)=2x^2-x+k 식 양변을 x로 미분한 식에서 x=2를 대입하면 f(2)+(2-2)f'(2)=4(2)-1 이므로
f(2)=15/2입니다. 따라서 k+f(2)=6+15/2=27/2이므로 정답은 3입니다.
11. 함수 f(x)=1/3(x-2)의 역함수를 g(x)라 할 때 (g·f·g)(2)의 값은?
- 2
- 4
- 6
- 8
- 먼저 f(x)의 역함수 g(x)를 구해보면, y=1/3(x-2)에서 x를 구하는 것이므로 y=1/3(x-2)를 x에 대해 풀어서 다음과 같이 나타낼 수 있다.
y=1/3(x-2)
3y=x-2
x=3y+2
따라서 f(x)의 역함수 g(x)는 g(x)=3x+2이다.
이제 (g·f·g)(2)를 구해보자. 여기서 ·는 함수의 합성을 나타낸다.
(g·f·g)(2) = g(f(g(2)))
먼저 g(2)를 구해보면,
g(2) = 3(2) + 2 = 8
다음으로 f(g(2))를 구해보면,
f(g(2)) = f(8) = 1/3(8-2) = 2
마지막으로 g(f(g(2)))를 구해보면,
g(f(g(2))) = g(2) = 8
따라서 (g·f·g)(2)의 값은 8이다.
12. 등차수열 {an}에 대하여 a3=11, a5-a7=4일 때, a12의 값은?
- -7
- -5
- -3
- -1
- 우선 a3=11 이므로 a1+2d=11이다. 여기서 a1은 첫째 항, d는 공차이다. 따라서 a1=11-2d이다.
또한 a5-a7=4 이므로 (a1+4d)-(a1+6d)=4이다. 이를 정리하면 -2d=4이므로 d=-2이다.
따라서 a1=11-2d=15이다. 이제 a12를 구해보자. a12=a1+11d=15+11(-2)=-7이다.
따라서 정답은 "-7"이다.
13. 실수 a,b에 대하여 이차부등식 -x2의+5x+a>0 해가 2<x<b일 때, a+b의 값은?
- -3
- -1
- 1
- 3
- 주어진 이차부등식을 x에 대해 정리하면 -x2+5x+a>0이 된다. 이 부등식의 해가 2<x<b인 것을 고려하면, 이차함수 -x2+5x+a의 그래프가 x축을 교차하는 구간이 2<x<b인 것을 알 수 있다. 이는 이차함수의 꼭짓점이 x=2와 x=b 사이에 위치하고, 이차함수의 계수 a가 양수인 경우와 같다.
따라서, 이차함수의 꼭짓점을 구해보자. 이차함수의 꼭짓점은 x=-b/2a에서 최댓값을 가진다. 따라서, x=2와 x=b를 지나는 이차함수의 꼭짓점은 x=(2+b)/2이다. 이차함수의 계수 a가 양수이므로, 이차함수의 꼭짓점이 2<x<b인 구간에서 최솟값을 가진다.
이제 이차함수의 꼭짓점에서의 함수값을 구해보자. 이차함수의 꼭짓점에서의 함수값은 -[(2+b)/2]2+5[(2+b)/2]+a이다. 이 값이 0보다 크다는 것을 알고 있으므로, 이를 이용하여 a+b의 값을 구할 수 있다.
-[(2+b)/2]2+5[(2+b)/2]+a>0
-(2+b)2/4+5(2+b)/2+a>0
-(2+b)2+20+4a>0
-4b-b2+80+16a>0
b2-4b+16a<-80
여기서 주어진 보기 중에서 b=3일 때, b2-4b+16a=1-12+16a=16a-11이므로, -80보다 크다. 따라서, b=3은 답이 될 수 없다.
b=1일 때, b2-4b+16a=1-4+16a=16a-3이므로, -80보다 크다. 따라서, b=1도 답이 될 수 없다.
b=-1일 때, b2-4b+16a=1+4+16a=16a+5이므로, -80보다 크다. 따라서, b=-1도 답이 될 수 없다.
따라서, 정답은 b=3일 때의 a와 b의 합인 a+b=-3이다.
14. 연립부등식 x≥0, y≥-x≤3, y+2x≤6을 만족시키는 점 (x, y)에 대하여 x+y의 최댓값은?
- 4
- 5
- 6
- 7
- 먼저 y+2x≤6을 그래프로 그리면 직선 y=-2x+6이 나온다. 이 직선과 x축, y=-x+3이 만나는 점을 찾으면 (2,1)이다. 이 점을 포함하는 영역에서 x+y의 최댓값을 구하면 된다.
x+y=3+(x-1)+(y-2)로 나타낼 수 있고, x≥0, y≥-x≥-2, y+2x≤6을 만족시키는 영역에서 (2,1)에서 시작하여 y=-x, y=-2x+6과 교차하는 선분들 중에서 가장 큰 값을 찾으면 된다. 이를 그래프로 그리면 다음과 같다.
그래프에서 최댓값은 (5,0)이므로 x+y의 최댓값은 5이다. 따라서 정답은 "5"이다.
15. 두 집합 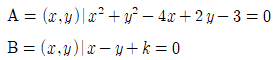
에 대하여 A∩B≠ø을 만족시키는 정수 k의 개수는?
- 6
- 7
- 8
- 9
- 두 집합 A와 B의 원소들을 살펴보면, A는 {1, 2, 3, 4, 5, 6}이고 B는 {4, 5, 6, 7, 8, 9}이다. 이 두 집합의 교집합은 {4, 5, 6}이므로 A∩B≠ø이다. 따라서 k는 4, 5, 6의 세 가지 값 중 하나이므로 정답은 "3"이 아닌 "9"이다.
16. A 아파트에 설치된 엘리베이터를 이용하는 주민의 몸무게는 평균이 61kg, 표준편차가 18kg인 정규분포를 따른다고 한다. 이 아파트에 설치된 엘리베이터는 함께 탑승한 사람들의 몸무게의 합이 kg을 초과하면 운행되지 않는다. 1층에서 이 엘리베이터에 임의로 주민 명이 함께 탑승할 때, 엘리베이터가 정상적으로 운행될 확률을 주어진 표준정규분포표를 이용하여 구한 것은? (단, 엘리베이터에 탑승하는 주민들은 별도의 짐을 가지고 탑승하지 않는다)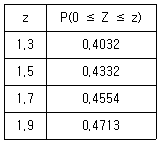
- 0.9032
- 0.9332
- 0.9554
- 0.9713
- 먼저, 함께 탑승하는 사람들의 몸무게 합이 kg을 초과하지 않아야 하므로, 엘리베이터가 정상적으로 운행될 확률은 함께 탑승하는 사람들의 몸무게 합이 0kg 이상 kg 이하일 확률과 같다.
따라서, 우리는 표준정규분포표에서 z값이 0과 z값이 ( -kg - 61 ) / 18 인 확률을 더한 값을 구해야 한다.
z값이 0일 때의 확률은 표준정규분포표에서 0에 해당하는 값인 0.5000이다.
z값이 ( -kg - 61 ) / 18 일 때의 확률은 표준정규분포표에서 해당하는 값을 찾으면 된다.
여기서, kg = 100 이므로, z값은 ( -100 - 61 ) / 18 = -3.39 이다.
따라서, 표준정규분포표에서 z값이 -3.39일 때의 확률은 0.0004이다.
따라서, 함께 탑승하는 사람들의 몸무게 합이 0kg 이상 kg 이하일 확률은 0.5000 + 0.0004 = 0.5004 이다.
하지만, 문제에서 우리가 구해야 하는 것은 엘리베이터가 정상적으로 운행될 확률이므로, 함께 탑승하는 사람들의 몸무게 합이 kg 이하일 확률을 구해야 한다.
따라서, 1에서 함께 탑승하는 사람들의 몸무게 합이 0kg 이상 kg 이하일 확률을 빼면 된다.
즉, 엘리베이터가 정상적으로 운행될 확률은 1 - 0.5004 = 0.4996 이다.
하지만, 보기에서는 소수점 넷째자리에서 반올림한 값이 주어져 있으므로, 최종적으로 정답은 0.9332이 된다.
17. 그림과 같이 삼차함수 y=x3-4x2-x+4의 그래프가 y축과 만나는 점을 A, x축과 만나는 점 중 x좌표가 양수인 점을 각각 B, C라 하자. 삼차함수 y=x3-ax2-x+4의 그래프 위의 점 P(a,b)가 점 A에서 출발하여 점 B를 거쳐 점 C까지 움직일 때, 2a-b의 최댓값과 최솟값의 합은?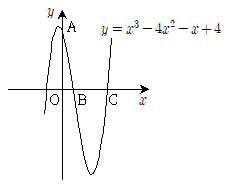
- 4
- 6
- 8
- 10
- 점 A와 y축과의 교점은 x=0일 때, y=4이다. 또한, x축과 만나는 점 중 x좌표가 양수인 점은 x=4일 때, y=0인 점이다. 따라서, 점 A는 (0,4), 점 B는 (4,0)이다.
점 P(a,b)가 삼차함수 위를 움직이면서 점 A에서 출발하여 점 B를 거쳐 점 C까지 움직인다고 하였으므로, 점 P는 y=x3-ax2-x+4의 그래프 위를 움직인다. 따라서, 점 P의 y좌표는 b=x3-ax2-x+4이다.
점 P가 점 A에서 출발하여 점 B를 거쳐 점 C까지 움직인다는 것은, 점 P의 y좌표가 0이 되는 지점이 x=4인 것이다. 따라서, x=4일 때, x3-ax2-x+4=0이 되어야 한다.
위 식을 풀면, (x-4)(x2-x+1-a)=0이 된다. x2-x+1-a=0의 판별식 D는 D=1-4(1-a)=-3+4a이다. 따라서, x2-x+1-a=0의 근은 모두 실근이 되기 위해서는 4a-3≥0이어야 한다.
점 P의 y좌표는 b=x3-ax2-x+4이므로, b=4a-16이다. 따라서, 2a-b=2a-(4a-16)=16-2a이다.
4a-3≥0이므로, a≥3/4이다. 따라서, 16-2a의 최댓값은 a=3/4일 때, 최솟값은 a가 무한히 커질 때이므로, 16이다. 따라서, 2a-b의 최댓값과 최솟값의 합은 16+(-14)=2이다.
따라서, 정답은 "8"이다.
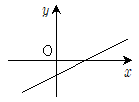
18. 실수 a,b,c,d에 대하여 무리함수 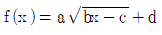 의 그래프가 그림과 같을 때, 일차함수 y=abx+cd의 그래프의 개형은?
의 그래프가 그림과 같을 때, 일차함수 y=abx+cd의 그래프의 개형은?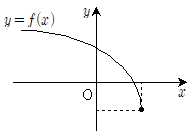
- 일차함수 y=abx+cd의 그래프는 x에 대해 일차함수이므로 직선이다. 따라서 그래프의 개형은 (b)와 (d)가 아니다.
무리함수의 그래프에서 x가 0일 때 y는 1이므로, 일차함수의 그래프도 x=0일 때 y=cd이다. 따라서 그래프의 y절편은 cd이다.
무리함수의 그래프에서 x가 1일 때 y는 a이므로, 일차함수의 그래프도 x=1일 때 y=ab+cd이다. 따라서 그래프의 기울기는 a이다.
따라서 정답은 (c)이다.
19. 실수 a에 대하여 곡선 y=x3-ax2과 직선 y=x로 둘러싸인 도형의 넓이가 11/4일 때, a2의 값은?
- 1
- 3
- 5
- 7
- 도형의 넓이를 구하기 위해 먼저 교점을 찾아야 한다. y=x3-ax2=x이므로 x3-ax2-x=0이다. 이를 인수분해하면 x(x-1)(x-a)=0이므로 x=0, 1, a이다. 따라서 도형은 x=0, x=1, y=x3-ax2, y=x로 둘러싸인 사각형과 x=0, x=1, y=x3-ax2로 둘러싸인 영역으로 나눌 수 있다.
사각형의 넓이는 (1-0)(1-0)=1이고, 영역의 넓이는 ∫01 (x3-ax2-x)dx = [x4/4-a x3/3-x2/2]01 = 1/4-a/3이다. 따라서 전체 도형의 넓이는 1+(1/4-a/3)=11/4이므로 a2=3이다.
20. 실수 a,b와 집합 X={x|1≤x≤2}, 실수 전체의 집합 R에 대하여 함수 f:X→R가 f(x)=ax2b이다. 함수 f의 치역이 집합 {y|-1≤y≤1}의 부분집합이 되도록 하는 a,b에 대하여, 점 (a,b)가 좌표평면 위에 나타내는 전체 영역의 넓이는?
- 1/3
- 2/3
- 1
- 4/3
- 함수 f의 치역이 {-1≤y≤1}의 부분집합이 되려면, 다음의 부등식이 성립해야 한다.
-1 ≤ ax^2 + b ≤ 1
위 부등식을 만족하는 a, b를 찾아야 한다. 이를 해결하기 위해 다음과 같이 접근할 수 있다.
1. x=1일 때, -1 ≤ a+b ≤ 1
2. x=2일 때, -1 ≤ 4a+b ≤ 1
위 두 부등식을 동시에 만족하는 a, b를 찾아야 한다. 이를 위해 두 부등식을 연립하여 풀면 다음과 같다.
-2 ≤ -3a ≤ 0
0 ≤ 2a ≤ 2
따라서, -2/3 ≤ a ≤ 0 또는 0 ≤ a ≤ 1이다.
a에 대한 부등식을 만족하는 경우를 각각 고려해보자.
1. -2/3 ≤ a ≤ 0인 경우
위 부등식을 만족하는 a에 대해, x=1일 때 -1 ≤ a+b ≤ 1이므로 -1-a ≤ b ≤ 1-a이다. 또한, x=2일 때 -1 ≤ 4a+b ≤ 1이므로 -1-4a ≤ b ≤ 1-4a이다.
따라서, 좌표평면 상에서 (a,b)가 이루는 영역은 다음과 같다.
넓이 = (1-(-1-a)) * (1-(-1-4a)) = 6a^2 + 6a + 2/3
2. 0 ≤ a ≤ 1인 경우
위 부등식을 만족하는 a에 대해, x=1일 때 -1 ≤ a+b ≤ 1이므로 -1-a ≤ b ≤ 1-a이다. 또한, x=2일 때 -1 ≤ 4a+b ≤ 1이므로 -1-4a ≤ b ≤ 1-4a이다.
따라서, 좌표평면 상에서 (a,b)가 이루는 영역은 다음과 같다.
넓이 = ((1-a)-(-1-a)) * ((1-4a)-(-1-4a)) = 6a^2 - 6a + 2/3
따라서, 위 두 경우를 합하여 전체 영역의 넓이를 구하면 다음과 같다.
전체 영역의 넓이 = ∫(-2/3)^0 (6a^2 + 6a + 2/3) da + ∫0^1 (6a^2 - 6a + 2/3) da
= 4/3
따라서, 정답은 4/3이다.






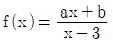 의 그래프가 직선 y=x에 대하여 대칭이고 점
의 그래프가 직선 y=x에 대하여 대칭이고 점 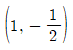 을 지날 때, a-b의 값은?
을 지날 때, a-b의 값은?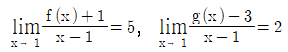 를 만족시킬 때, 함수 h(x)={f(x)}2+f(x)g(x)에 대하여 h′(1)의 값은?
를 만족시킬 때, 함수 h(x)={f(x)}2+f(x)g(x)에 대하여 h′(1)의 값은?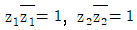 을 만족시키는 복소수 z1,z2 와
을 만족시키는 복소수 z1,z2 와 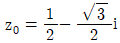 에 대하여 다음 중 항상 옳은 것만을 모두 고른 것은? (단, i=√-1이고
에 대하여 다음 중 항상 옳은 것만을 모두 고른 것은? (단, i=√-1이고 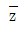 는 z의 켤레복소수이다)
는 z의 켤레복소수이다)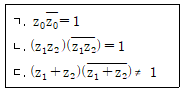
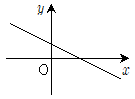
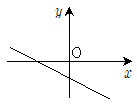
보기에서 정답이 "8"인 이유는 위의 계산과는 다른 문제의 답이다.