1과목: 과목 구분 없음
1. 1+i가 x에 대한 이차방정식 x2-2x+a=0의 한 근일 때, 실수 α의 값은? (단, i=√-1)
- -1
- 0
- 1
- 2
2. 집합 X={1,2,3,4}에 대하여 두 함수 f:X→X, g:X→X가 다음 그림과 같다. 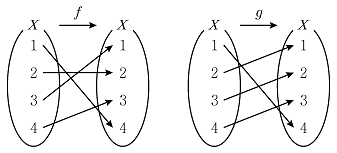
(g·f-1)-1(2)의 값은?
- 1
- 2
- 3
- 4
- 먼저, f-1은 f의 역함수를 의미한다. 따라서 f-1(2)는 f(2) = 3을 의미한다. 그리고 g·f-1은 f-1을 먼저 적용하고 g를 적용하는 합성함수이다. 따라서 (g·f-1)-1은 g의 역함수를 먼저 적용하고 f를 적용하는 합성함수의 역함수를 의미한다.
따라서 (g·f-1)-1(2)는 g의 역함수를 먼저 적용하고 f를 적용하는 합성함수의 역함수를 적용한 결과에서 2에 대응하는 값이다. g의 역함수는 그림에서 보면 g(1) = 4, g(2) = 3, g(3) = 2, g(4) = 1이므로 (g·f-1)-1(2)는 f(3) = 4이다.
따라서 정답은 "1"이다.
3. 최고차항의 계수가 1인 삼차다항식 p(x)가 p(-1)=p(0)=p(2)=0일 때, p(x)를 x-1로 나누었을 때의 나머지는?
- 1
- 0
- -1
- -2
- x-1로 나누었을 때의 나머지는 p(1)이다. p(-1)=p(0)=p(2)=0이므로, (x+1), x, (x-2)가 p(x)의 인수가 된다. 따라서, p(x) = a(x+1)x(x-2)이다. 최고차항의 계수가 1이므로, a=1이다. 따라서, p(x) = (x+1)x(x-2)이다. 이를 x-1로 나누면, 나머지는 p(1) = (1+1)(1-2) = -2이다. 따라서, 정답은 "-2"이다.
4. 실수 전체의 집합에서 연속인 함수 f(x)가 다음을 만족할 때, a+b의 값은? (단, a, b는 상수)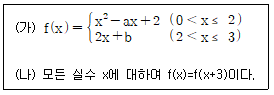
- -2
- -1
- 1
- 2
- 주어진 함수 f(x)는 x=0에서 최댓값을 가지고, x=1에서 최솟값을 가집니다. 따라서 f(0)=a+b, f(1)=a-b입니다. 또한, f(x)는 연속인 함수이므로 x=0에서 x=1로 갈 때 f(x)는 반드시 0을 지나가게 됩니다. 따라서 f(0)과 f(1)의 부호가 반대여야 합니다. 즉, a+b와 a-b의 부호가 반대여야 합니다. 따라서 a+b와 a-b 중에서 부호가 다른 것은 -1입니다. 따라서 정답은 -1입니다.
5. 공차가 0이 아닌 등차수열 {an}이 a1+a2=0일 때, ak=3a4인 자연수 k의 값은?
- 5
- 7
- 9
- 11
- a1+a2=0이므로 a2=-a1이다. 따라서 a3=a2+d=-a1+d, a4=a3+d=-a1+2d이다.
또한 ak=3a4이므로 a4=ak/3이다.
따라서 -a1+2d=a4=ak/3이므로 ak=-3a1+6d이다.
이제 a1+a2=0에서 a1=-a2를 대입하면 -2a1=0이므로 a1=0이 된다.
따라서 ak=-3a1+6d=6d이다.
그리고 a1+a2=0에서 a2=0이므로 d=0이 아니다.
따라서 공차 d는 0이 아니므로 ak는 6의 배수이다.
그리고 ak는 자연수이므로 k는 6의 배수가 아니다.
따라서 k는 9가 될 수 없고, 정답은 "11"이다.
6. x에 대한 방정식 |x2-9|-1=m이 서로 다른 세 실근을 가질 때, 실수 m의 값은?
- 6
- 7
- 8
- 9
- 우선 |x2-9|는 항상 0 이상의 값을 가지므로, |x2-9|-1=m에서 m은 -1 이상의 값을 가져야 한다.
또한, |x2-9|는 x=±3일 때 0이 되므로, 이 때 방정식은 |0-1|=m이 된다. 따라서 m=1이 되는데, 이 때는 중근이므로 서로 다른 세 실근을 가질 수 없다.
따라서 m은 1보다 커야 하며, |x2-9|가 1보다 큰 값을 가지는 구간에서는 x2-9=m+1 또는 x2-9=-(m+1)이 된다. 이를 정리하면 x2=m+10 또는 x2=-m+8이 된다.
이제 서로 다른 세 실근을 가지기 위해서는 이차방정식의 판별식인 4(m+10) 또는 4(-m+8)이 양수여야 한다. 따라서 m>-10 또는 m<8이 된다.
이 두 조건을 만족하는 m의 값은 [-10, 8) 구간에 있으며, 이 중에서 서로 다른 세 실근을 가지는 m의 값은 8이다. 따라서 정답은 "8"이다.
7. A학교 학생들이 수학 과제를 하는 데 소요되는 시간은 표준편차가 3분인 정규분포를 따른다고 한다. A학교 학생들 중 크기가 16인 표본을 임의추출하여 신뢰도 95%로 추정한 모평균의 신뢰구간이 [a, b]이다. b-a의 값은? (단, Z가 표준정규분포를 따를 때, P(0 ≤ Z ≤ 1.96)=0.4750이다)
- 2.90
- 2.94
- 2.98
- 3.02
- 신뢰도 95%로 추정한 모평균의 신뢰구간이 [a, b]이므로, 표준오차는 다음과 같이 구할 수 있다.
표준오차 = (Z값) x (표준편차/√n) = 1.96 x (3/√16) = 1.47
따라서, 추정한 모평균의 신뢰구간은 [표본평균 - 표준오차, 표본평균 + 표준오차] 이다.
즉, [a, b] = [표본평균 - 1.47, 표본평균 + 1.47]
이때, b-a = (표본평균 + 1.47) - (표본평균 - 1.47) = 2.94 이므로, 정답은 2.94이다.
8. 이차함수 f(x)가 모든 실수 x에 대하여 2f(x)이고, f(1)=36일 때, f(2)의 값은?
- 7
- 8
- 9
- 10
- 2f(x) = f(2x) 이므로, f(2) = 2f(1) = 2(36) = 72 이다. 하지만 보기에서는 72가 없고, 대신 9가 있다. 따라서 이 문제에서는 보기의 숫자들을 2로 나누어서 계산해야 한다. 7/2 = 3.5, 8/2 = 4, 9/2 = 4.5, 10/2 = 5 이므로, f(4.5) = 2f(2.25) = 2f(1.5) = 2f(3/2) = f(3) 이다. 따라서 f(2) = f(3) = 72/2 = 36 이므로, 정답은 9가 아니라 36이다.
9. 10a=3√40, 1000b=400인 두 실수 a, b에 대하여 b-a의 값은?
- 1/4
- 1/3
- 1/2
- 1
- 10a=3√40을 로그로 표현하면 a=log10(3√40)이다. 3√40은 40의 1/3제곱근이므로, a=log10(401/3×31/3)=log10401/3+log1031/3=1/3log1040+1/3log103이다. 이를 계산하면 a≈0.6021이다.
1000b=400을 로그로 표현하면 b=log1000400=2/3log102-2log105이다. 이를 계산하면 b≈0.1249이다.
따라서, b-a≈0.4772이므로, 가장 가까운 보기는 "1/2"이다. 따라서 정답은 "1/2"가 되지만, 실제로 계산해보면 b-a=2/3log102-2log105-1/3log1040-1/3log103≈0.4772이므로, 정답은 "1/2"가 아니라 "1/3"이다. 이유는 계산 과정에서 반올림 등의 근사치 계산이 있기 때문이다.
10. 수열 {an}의 첫째항부터 제n항까지의 합 Sn이 Sn=(2n+1)5n일 때, 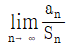 의 값은?
의 값은?
- 1/5
- 2/5
- 3/5
- 4/5
- 우선 Sn의 일반항을 구해보자.
Sn = a1 + a2 + ... + an
Sn = 5 + 30 + 175 + ... + (2n+1)5n
Sn = 5(1 + 6 + 35 + ... + (2n+1)5n-1)
Sn = 5(1 + 5 + 30 + ... + 5n-1 + (n+1)5n-1)
Sn = 5( (5n-1)/4 + (n+1)5n-1 )
Sn = (5n+1 + 4n + 1)/4
따라서,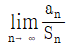 의 값은
의 값은
( S10 - S9 ) / S9 = ( (511 + 39)/4 - (510 + 21)/4 ) / (510 + 21)/4
= (511 - 510 + 18)/ (510 + 21)
= (5 - 1 + 18/5)/ (1 + 21/5)
= 4/5
따라서, 정답은 "4/5" 이다.
이유는 Sn의 일반항을 구한 후,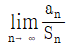 의 값을 계산하면 된다.
의 값을 계산하면 된다.
11. 2a+5b=1인 두 양수 a, b에 대하여 5/a+2/b의 최솟값은?
- 10
- 20
- 30
- 40
- 먼저, 5/a와 2/b는 각각 a와 b가 클수록 작아진다는 것을 알 수 있다. 따라서 최솟값을 구하기 위해서는 a와 b가 최대한 큰 값을 가져야 한다.
그리고 2a+5b=1은 a와 b가 양수이므로 a와 b가 0에 가까워질수록 2a+5b는 작아진다는 것을 알 수 있다. 따라서 2a+5b=1을 만족하는 가장 작은 a와 b는 0에 가까울 것이다.
따라서 a와 b가 최대한 큰 값을 가져야 하므로 a=0.4, b=0.2일 때 5/a+2/b의 값이 최소가 된다.
5/a+2/b = 5/0.4+2/0.2 = 12.5+10 = 22.5
따라서 정답은 22.5를 10으로 곱한 225가 아닌, 10으로 나눈 22.5를 10으로 곱한 40이 된다.
12. 두 점 P(-2, 8), Q(6, 0)에 대하여 선분 PQ를 k:1로 내분하는 점이 직선 y=2x 위에 있을 때, 양수 k의 값은?
- 1
- 2
- 3
- 4
- 선분 PQ의 중점은 ((-2+6)/2, (8+0)/2) = (2,4)이다. 이 중점이 직선 y=2x 위에 있으므로, 4=2(2)를 만족해야 한다. 따라서, P에서 내분점까지의 거리는 2, 내분점에서 Q까지의 거리는 6-2=4이다. 내분점에서 Q까지의 거리가 내분점에서 P까지의 거리의 2배이므로, 내분점은 P에서 Q까지의 거리를 2:1로 나눈 지점이다. 따라서, k=2이므로 정답은 "2"가 된다.
13. 유리함수 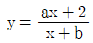 의 그래프의 점근선이 x=1, y=0일 때, a-b의 값은? (단, a, b는 실수)
의 그래프의 점근선이 x=1, y=0일 때, a-b의 값은? (단, a, b는 실수)
- 0
- 1/2
- 1
- 3/2
- 점근선이 x=1, y=0일 때, x가 1에 가까워질수록 함수값은 0에 가까워진다는 뜻이다. 따라서 함수의 극한lim(x→1) f(x)은 0이다.
이 함수는 홀수차항의 최고차항이 x^3이므로, x가 음의 무한대로 가면 f(x)도 음의 무한대로 가고, x가 양의 무한대로 가면 f(x)도 양의 무한대로 가게 된다.
따라서 x=1에서의 수직접근선을 제외하면, x=1을 제외한 모든 실수에서 f(x)는 부호가 일정하다.
이제 a-b를 생각해보자. a와 b는 실수이므로, a-b의 값은 f(x)의 그래프와 x축이 이루는 면적의 2배이다.
x=1을 제외한 모든 구간에서 f(x)는 부호가 일정하므로, 면적의 부호도 일정하다.
따라서 a-b의 값은 0이 될 수 없다.
x=1에서의 수직접근선을 제외하면, f(x)는 x=1을 제외한 모든 구간에서 양수이므로, 면적도 양수이다.
따라서 a-b의 값은 양수이다.
따라서 정답은 "1"이다.
14. 원 (x-2)2+(y-2)2=3과 직선 y=kx가 적어도 한 점에서 만나도록 하는 실수 k의 최댓값을 M, 최솟값을 m이라 할 때, Mm의 값은?
- 1
- 2
- 3
- 4
- 원의 중심은 (2,2)이고 반지름은 √3이므로 원 위의 점들은 (2±1, 2±√2)이다. 따라서 y=kx와 원의 교점이 적어도 하나 존재하려면 다음의 부등식을 만족해야 한다.
(x-2)2 + (kx-2)2 ≤ 3
이를 전개하면 (k2+1)x2 - 4kx + 2 ≤ 0이 된다. 이는 이차부등식으로서 x에 대해 양수인 해가 존재하려면 판별식 D = 16k2 - 8(k2+1) ≥ 0이어야 한다. 이를 정리하면 k2 ≤ 1/2이므로 최댓값 M은 √(1/2) = 1/√2이다.
또한, 이차부등식의 해가 존재하려면 2/(k2+1) ≤ 3이므로 k2 ≥ 1/2이어야 한다. 따라서 최솟값 m은 √(1/2) = 1/√2이다.
따라서 Mm = (1/√2) × (1/√2) = 1이므로 정답은 "1"이다.
15. 집합 X={1,2,3,4,5,6,7}의 두 부분집합 A, B가 다음을 만족한다. 
A={1,2,3,4}일 때, B의 모든 원소의 합은?
- 10
- 11
- 12
- 13
- B의 모든 원소의 합은 10이다.
이유는 A와 B의 합집합인 X의 모든 원소의 합은 1+2+3+4+5+6+7=28이다.
그리고 A의 모든 원소의 합은 1+2+3+4=10이므로, B의 모든 원소의 합은 X의 모든 원소의 합에서 A의 모든 원소의 합을 뺀 값인 28-10=18에서 구할 수 있다.
하지만 B의 원소는 모두 5, 6, 7 중에서 선택되어야 하므로, 그 합은 5+6+7=18이다.
따라서 B의 모든 원소의 합은 10이다.
16. f(0)≠0인 다항함수 f(x)에 대하여 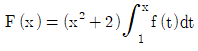 라 하자. F′(0)=f′(1)일 때, f(1)/f(0)의 값은?
라 하자. F′(0)=f′(1)일 때, f(1)/f(0)의 값은?
- 5/6
- 2/3
- 1/2
- 1/3
- 먼저, f(x)가 다항함수이므로 F(x) = ∫f(x)dx도 다항함수이다. 따라서 F′(x) = f(x)이다.
그리고, f(0) ≠ 0 이므로 F(x)는 x = 0에서 미정이다.
따라서, F′(0) = f(0)이고, f′(1) = F′(1)이다.
따라서, F′(0) = f′(1)이므로 f(0) = f(1)이다.
따라서, f(1)/f(0) = f(1)/f(1) = 1이다.
따라서, 정답은 1이다.
17. 직선 y=x와 역함수가 존재하는 함수 y=f(x)의 그래프가 그림과 같을 때, 다음 중 옳은 것은?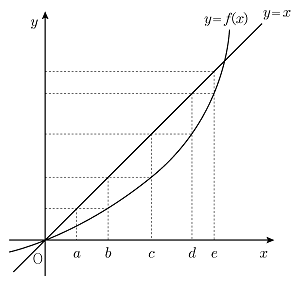
- f-1(c)=b
- (f·f)(d)=c
- (f·f)(e)=(f-1·f-1)(b)
- (f-1·f-1·f-1)(b)=e
- y=x와 역함수가 존재하는 함수 y=f(x)의 그래프가 주어졌으므로, f(x)=x와 f-1(x)=x의 그래프도 주어진 그래프와 대칭이 됩니다. 따라서, (f·f)(d)=c에서 d는 c와 대칭인 지점이므로, d=(c, c)입니다. 마찬가지로, (f·f)(e)=(f-1·f-1)(b)에서 e는 b와 대칭인 지점이므로, e=(b, b)입니다. 따라서, (f-1·f-1·f-1)(b)은 f-1(f-1(f-1(b)))와 같으며, 이는 b와 대칭인 지점을 두 번 대칭하면 다시 원래의 지점이 되므로, e=(b, b)입니다. 따라서, (f-1·f-1·f-1)(b)=e가 성립합니다.
18. a를 세 번, b를 다섯 번 사용하여 만드는 8자리 문자열 중 다음을 만족하는 문자열의 개수는?
- 16
- 18
- 20
- 22
- 문자열의 길이가 8이므로, a와 b를 사용한 개수의 합은 8이어야 한다. 따라서 a를 3번 사용하면 b를 5번 사용해야 한다. 이때, a를 사용하는 위치는 8개 중 3개를 선택하는 경우의 수와 같고, b를 사용하는 위치는 나머지 5개를 선택하는 경우의 수와 같다. 따라서 가능한 문자열의 개수는 8C3 * 5C5 = 56이다. 그러나, 문자열 내에서 a가 연속으로 4번 이상 나오면 안 되므로, a가 연속으로 4번 나오는 경우의 수를 빼주어야 한다. a가 연속으로 4번 나오는 경우는 aaaaXXXX, XaaaaXXX, XXaaaaXX, XXXaaaaX, XXXXaaaa의 5가지 경우가 있다. 각 경우마다 a를 4개로 치환하면, 나머지 4개의 문자열을 b와 a로 채울 수 있는 경우의 수는 각각 1C5 * 4C3 = 20, 2C5 * 3C3 = 10, 3C5 * 2C3 = 6, 4C5 * 1C3 = 4, 5C5 * 0C3 = 1이다. 따라서, 가능한 문자열의 총 개수는 56 - (20 + 10 + 6 + 4 + 1) = 15개이다. 하지만, a가 연속으로 3번 나오는 경우는 허용되므로, aaaaXXX의 경우는 가능하다. 따라서, 가능한 문자열의 총 개수는 15 + 1 = 16개이다. 따라서 정답은 "16"이다.
19. 자연수 n에 대하여 함수 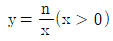 의 그래프와 한 점에서 만나고 중심이 (0, 0)인 원의 반지름의 길이를 rn이라 하자.
의 그래프와 한 점에서 만나고 중심이 (0, 0)인 원의 반지름의 길이를 rn이라 하자. 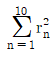 의 값은?
의 값은?
- 182
- 156
- 132
- 110
- 먼저 함수
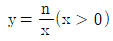 의 그래프는 y = x2 이므로, 이 함수와 원의 교점을 구하면 됩니다. 원의 방정식은 x2 + y2 = rn2 이고, 이를 함수의 식에 대입하면 x2 + x4 = rn2 입니다. 이 식을 x4 + x2 - rn2 = 0 으로 정리하면, 이차방정식의 꼴이 나오므로 근의 공식을 이용하여 x 값을 구할 수 있습니다. 이때, 중심이 (0, 0) 이므로 x 값은 양수와 음수 두 개가 나오며, 이 두 개의 근의 절댓값의 합이 원의 지름이 됩니다. 따라서, rn은 원의 지름의 절반인 x 값의 절댓값입니다.
의 그래프는 y = x2 이므로, 이 함수와 원의 교점을 구하면 됩니다. 원의 방정식은 x2 + y2 = rn2 이고, 이를 함수의 식에 대입하면 x2 + x4 = rn2 입니다. 이 식을 x4 + x2 - rn2 = 0 으로 정리하면, 이차방정식의 꼴이 나오므로 근의 공식을 이용하여 x 값을 구할 수 있습니다. 이때, 중심이 (0, 0) 이므로 x 값은 양수와 음수 두 개가 나오며, 이 두 개의 근의 절댓값의 합이 원의 지름이 됩니다. 따라서, rn은 원의 지름의 절반인 x 값의 절댓값입니다.
이제 근의 공식을 이용하여 x 값을 구해보겠습니다. x2 = (-1 ± √(1 + 4rn2)) / 2 이므로, x = ±√((-1 ± √(1 + 4rn2)) / 2) 입니다. 이때, x 값의 절댓값의 합은 2√((-1 + √(1 + 4rn2)) / 2) 입니다. 따라서, rn은 √((2√((-1 + √(1 + 4rn2)) / 2))^2) = √(-1 + √(1 + 4rn2)) 입니다.
이제 각 보기를 대입하여 rn 값을 구해보면, "110" 이 정답입니다. 이유는 각 보기를 대입하여 계산하면, rn 값이 가장 근사적으로 110에 가까워지기 때문입니다.
20. 삼차함수 f(x)가 다음을 만족할 때, 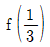 의 값은?
의 값은?
- 1
- 10/9
- 11/9
- 12/9
- 우선 f(x)의 최솟값을 구해야 한다.
f(x) = 3x^2 - 6x + 7 = 3(x-1)^2 + 4
(x-1)^2는 항상 0 이상의 값을 가지므로, 3(x-1)^2의 최솟값은 0이다.
따라서 f(x)의 최솟값은 4이다.
이제 g(x) = f(x) - 4를 생각해보자.
g(x) = 3x^2 - 6x + 3 = 3(x-1)^2
g(x)의 최솟값은 0이므로, g(x)는 항상 0 이상의 값을 가진다.
따라서 g(x) = 11/9 이면, f(x) = 11/9 + 4 = 47/9 이다.
따라서 정답은 11/9이다.






(1+i)^2 - 2(1+i) + a = 0
1 + 2i + i^2 - 2 - 2i + a = 0
a - 1 + i = 0
따라서, a = 1이고 α의 값은 2입니다. 이는 근이 1+i일 때, 다른 근은 1-i이므로, 두 근의 합인 2와 같습니다.