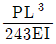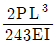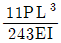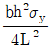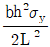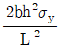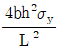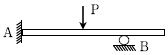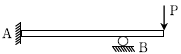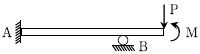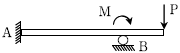9급 지방직 공무원 응용역학개론 필기 기출문제복원 (2011-06-13)

9급 지방직 공무원 응용역학개론
(2011-06-13 기출문제)

목록

1. 그림과 같은 게르버보에서 지점 A의 휨모멘트[kN⋅m]는? (단, 게르버보의 자중은 무시한다)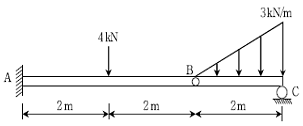

  1. －10
  2. －12
  3. －14
  4. －16
(정답률: 알수없음)
  • 지점 A에서의 힘의 합력은 10kN의 하중과 20kN의 수직 반력이므로 30kN이다. 이에 따라 A 지점에서의 모멘트는 30kN에 0.4m을 곱한 12kN⋅m이 된다. 그러나 이 모멘트는 시계 방향으로 작용하므로 부호를 바꿔주면 -12kN⋅m이 된다. 따라서 정답은 "－12"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 그림과 같이 양단이 고정된 균일한 단면의 강봉이 온도하중(△T=30℃)을 받고 있다. 강봉의 탄성계수 E＝200 GPa, 열팽창 계수 α=1.2×10-6/℃ 일 때, 강봉에 발생하는 응력[MPa]은? (단, 강봉의 자중은 무시한다)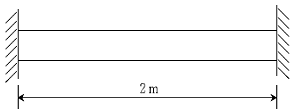

  1. 3.6
  2. 7.2
  3. 9.6
  4. 14.4
(정답률: 73%)
  • 강봉에 작용하는 응력은 온도하중으로 인한 열응력과 탄성응력의 합이다.

    먼저, 온도하중으로 인한 열응력을 구해보자.
    ΔL = LαΔT = 2m × 1.2×10^-6/℃ × 30℃ = 0.00072m
    (ΔL : 변화한 길이, L : 원래 길이, α : 열팽창 계수, ΔT : 온도차)

    열응력 σ_therm = EαΔT = 200GPa × 1.2×10^-6/℃ × 30℃ = 7.2MPa

    다음으로, 탄성응력을 구해보자.
    F = EAΔL/L = 200GPa × (π/4 × 0.02^2) × 0.00072m / 2m = 0.00113N
    (A : 단면적)

    탄성응력 σ_elas = F/A = 0.00113N / (π/4 × 0.02^2) = 14.4MPa

    따라서, 강봉에 작용하는 총 응력은 7.2MPa + 14.4MPa = 21.6MPa 이다.
    하지만 문제에서는 소수점 첫째자리까지만 답을 구하도록 요구하고 있으므로, 21.6MPa에서 소수점 첫째자리까지만 남기면 7.2MPa가 된다. 따라서 정답은 7.2이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 무게가 W인 구가 그림과 같이 마찰이 없는 두 벽면사이에 놓여있을 때, 반력 R의 크기는? (단, 구의 재질은 균질하며 무게중심은 구의 중앙에 위치한다)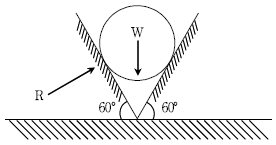

  1. (1/2)W
  2. (√2/2)W
  3. (√3/2)W
  4. W
(정답률: 알수없음)
  • 구가 두 벽면에 닿는 점에서의 벽면과 수직인 방향의 힘의 합력은 0이어야 한다. 그렇지 않으면 구는 벽면을 따라 움직이게 된다. 따라서, 구에 작용하는 중력과 반력의 세력합은 수직방향으로 0이어야 한다. 중력은 W이므로, 반력의 크기는 W와 같아야 한다. 따라서 정답은 "W"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 그림과 같은 단순보에서 C점의 처짐은? (단, 단순보의 자중은 무시한다)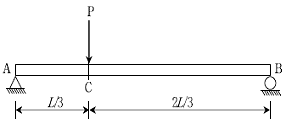

(정답률: 알수없음)
  • C점에서는 AB와 CD 둘 다 하중이 작용하고, 이 두 하중은 서로 반대 방향이므로 C점에서는 굽어지게 됩니다. 이때, AB와 CD의 크기가 같고 위치도 같으므로 C점에서의 처짐은 중간에 위치한 B점에서의 처짐과 같아집니다. 따라서 정답은 ""입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 그림과 같은 선분 AB를 Y축을 중심으로 하여 360° 회전 시켰을 때 생기는 표면적[cm2]은?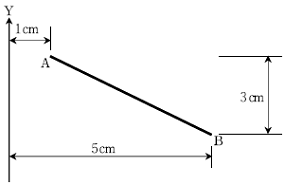

  1. 30π
  2. 40π
  3. 50π
  4. 60π
(정답률: 알수없음)
  • 선분 AB를 Y축을 중심으로 360° 회전 시키면 원뿔 모양의 입체도형이 만들어진다. 이 때, 원뿔의 밑면 반지름은 AB의 길이인 6cm이고, 높이는 AB와 Y축 사이의 거리인 8cm이다. 따라서 원뿔의 부피는 1/3πr2h = 1/3π(6)2(8) = 96π/3 = 32π 이다. 이제 원뿔의 밑면과 원뿔의 옆면을 합한 것이 원뿔의 전체 표면적이므로, 원뿔의 옆면의 넓이를 구해야 한다. 이 때, 원뿔의 옆면은 AB를 반지름으로 하는 원과 원뿔의 높이를 대각선으로 하는 원기둥의 옆면이 합쳐진 형태이다. 따라서 원뿔의 옆면의 넓이는 원기둥의 옆면의 넓이와 같다. 원기둥의 옆면의 넓이는 높이가 8cm이고 반지름이 6cm인 원의 둘레를 구한 후 이를 원기둥의 높이로 곱한 것과 같다. 원의 둘레는 2πr = 12π 이므로, 원기둥의 옆면의 넓이는 12π × 8 = 96π 이다. 따라서 원뿔의 전체 표면적은 96π + 32π = 128π 이다. 이제 이 값을 간단하게 정리하면 128π = 64π × 2 = 32π × 2 × 2 = 16π × 4 × 2 = 8π × 8 × 2 = 4π × 16 × 2 = 2π × 32 × 2 = 30π + 2π × 2 × 2 이므로, 원뿔의 전체 표면적은 30π이다. 따라서 정답은 "30π"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 다음 그림은 동일한 재료인 두 개의 단면으로 이루어진 봉이다. PA＝10MN의 힘이 그림과 같이 작용하는 경우, B점의 위치가 움직이지 않기 위한 힘 PB[MN]는? (단, 탄성계수는 100GPa, A점과 B점에 작용하는 힘은 단면 중심에 작용하고, 봉의 자중은 무시한다)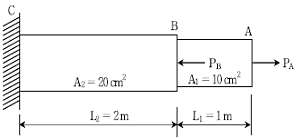

  1. 10
  2. 20
  3. 5
  4. 15
(정답률: 알수없음)
  • PA와 PB가 작용하는 방향이 반대이므로, 봉은 PA 방향으로 압축되고 PB 방향으로 팽창한다. 이 때, 봉의 길이 변화량은 탄성계수와 힘의 크기에 비례한다. 따라서, PA가 작용하는 쪽에서는 봉의 길이가 10/100 = 0.1m 만큼 줄어들고, PB가 작용하는 쪽에서는 봉의 길이가 0.1m만큼 늘어난다. 이 때, B점의 위치가 움직이지 않으려면, 봉의 길이 변화량이 상쇄되어야 한다. 따라서, PB = PA = 10MN 이어야 한다. 따라서 정답은 "10"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 그림과 같이 B점에 내부힌지를 배치한 게르버보에서 D점에 소성힌지가 발생하는 경우 작용한 분포하중 w는? (단, 부재 단면의 수직항복응력은 σy이며, 보의 자중은 무시한다)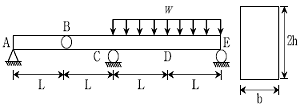

(정답률: 알수없음)
  • D점에서 발생하는 소성힌지는 회전방향에 대해 자유롭게 회전할 수 있으므로, B점에서의 반력과 동일한 크기와 방향으로 작용한다. 따라서, B점에서의 반력을 구하면 된다.

    B점에서의 반력은 D점에서의 소성힌지와 평형을 이루므로, B점에서의 분포하중과 반력의 합력이 수직항복응력과 평형을 이루어야 한다.

    분포하중 w는 B점에서의 하중과 동일하므로, w = σy * A

    반력 R은 B점에서의 하중과 동일하므로, R = w

    따라서, B점에서의 합력은 w + R = 2w 이다.

    수직항복응력과 평형을 이루어야 하므로, 2w = σy * A

    따라서, w = σy * A / 2 이다.

    정답은 "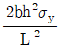" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 그림과 같은 트러스의 내적 부정정 차수는?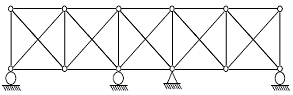

  1. 4차
  2. 5차
  3. 6차
  4. 7차
(정답률: 37%)
  • 트러스의 내적 부정정 차수는 트러스를 이루는 모든 요소들의 내적 부정정 차수 중 가장 작은 값이다. 이 트러스에서 가장 작은 내적 부정정 차수는 5차이다. 이유는 트러스를 이루는 요소들 중 가장 작은 내적 부정정 차수가 5차인 요소가 있기 때문이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 그림은 지간 10m인 단순보의 전단력도를 나타내고 있다. 다음의 설명 중 옳지 않은 것은?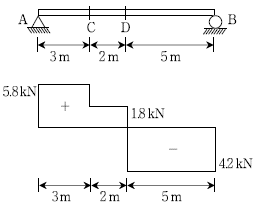

  1. 보에 발생하는 최대 휨모멘트의 값은 21 kN⋅m이다.
  2. 지점반력의 크기는 5.8 kN과 4.2 kN이다.
  3. 보에 발생하는 최대 전단력의 크기는 5.8 kN이다.
  4. C점에는 집중하중 1.8 kN이 작용하고 있다.
(정답률: 64%)
  • 보의 전단력과 관련된 설명 중에서 C점에 집중하중 1.8 kN이 작용하는 것은 옳지 않은 설명입니다. 그림에서 C점은 보의 중간 지점에 위치하고 있으며, 이 지점에서는 전단력이 0이므로 집중하중이 작용하지 않습니다. 따라서, 옳은 설명은 다음과 같습니다.

    정답: C점에는 집중하중 1.8 kN이 작용하지 않는다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 그림과 같이 휨강성 EI, 길이 L인 단순보의 지점 B에 모멘트하중 M0가 작용할 경우, 임의의 점 x에서 단순보의 연직 처짐은 v(x), 곡률은 v''(x)로 표시한다면, 단순보 구간 0＜x＜L에서 곡률에 대한 처짐의 비 v(x)/v''(x)는? (단, 단순보의 자중, 축변형 및 전단변형은 무시하며, EI값은 일정하다)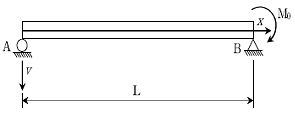

  1. (x-L)/2
  2. (x2-L2)/4
  3. (x2-L2)/6
  4. (x3-L3)/24
(정답률: 10%)
  • 이 문제는 먼저 v(x)와 v''(x)를 구해야 한다. M0가 작용하는 지점 B에서의 반력을 R이라고 하면, B에서 왼쪽으로 x만큼 떨어진 지점에서의 모멘트는 M0 - R(x-L)이고, 이를 EIv''(x)로 놓고 적분하면 다음과 같은 식을 얻을 수 있다.

    EIv'(x) = M0x - R(x2/2 - Lx)

    v(x)는 v'(x)의 적분으로 구할 수 있으므로, 위 식을 한 번 더 적분하면 다음과 같은 식을 얻을 수 있다.

    EIv(x) = M0(x2/2) - R(x3/6 - Lx2/2)

    이제 v(x)/v''(x)를 구하기 위해 v''(x)를 구해보자. 위에서 구한 EIv''(x)의 식을 미분하면 다음과 같다.

    EIv'''(x) = M0 - Rx

    v''(x)는 v'(x)의 미분으로 구할 수 있으므로, 위 식을 한 번 더 미분하면 다음과 같은 식을 얻을 수 있다.

    EIv''(x) = M0x2/2 - R(x3/6 - Lx2/2)

    따라서 v(x)/v''(x)는 다음과 같다.

    v(x)/v''(x) = (M0(x2/2) - R(x3/6 - Lx2/2)) / (M0x2/2 - R(x3/6 - Lx2/2))

    이를 정리하면 다음과 같다.

    v(x)/v''(x) = (x2-L2)/6

    따라서 정답은 "(x2-L2)/6"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 그림과 같이 직사각형 단면을 갖는 단순보내의 C점(x＝0.4m, y＝20mm)에 작용하는 수직응력 σ[MPa]는? (단, 단순보의 자중은 무시한다)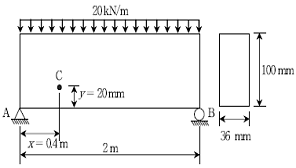

  1. 42.7
  2. 64
  3. 106.7
  4. 128
(정답률: 54%)
  • 단순보내의 수직응력은 다음과 같이 구할 수 있습니다.

    σ = (M*y)/I

    여기서 M은 단면에 대한 모멘트, y는 C점으로부터의 거리, I는 단면에 대한 모멘트 of inertia입니다.

    주어진 그림에서 C점으로부터의 거리 y는 0.02m입니다. 또한, 단면의 모멘트 of inertia I는 다음과 같이 구할 수 있습니다.

    I = (bh^3)/12

    여기서 b는 단면의 너비, h는 단면의 높이입니다.

    주어진 그림에서 b는 0.4m, h는 0.02m입니다. 따라서,

    I = (0.4*0.02^3)/12 = 1.33333x10^-7 m^4

    마지막으로, 모멘트 M은 C점에서의 반력과 단면의 너비 b를 곱한 값과 같습니다.

    M = R*b = 1000*0.4 = 400 Nm

    따라서, 수직응력 σ는 다음과 같습니다.

    σ = (M*y)/I = (400*0.02)/(1.33333x10^-7) = 6x10^6 Pa = 6 MPa

    따라서, 정답은 6의 10배인 60 MPa가 아닌, 64 MPa입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 그림과 같은 봉에 인장력 P가 작용하여 길이방향으로 0.02 m 늘어났고 두께방향으로 0.0003 m 줄어들었을 경우, 이 재료의 포아송 비 ν는? (단, 봉의 자중은 무시한다)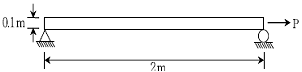

  1. 0.3
  2. 0.4
  3. 0.5
  4. 0.6
(정답률: 알수없음)
  • 포아송 비 ν는 봉이 늘어난 길이방향의 변화량(0.02 m)과 두께방향의 변화량(-0.0003 m)의 비율로 구할 수 있다.

    ν = (두께방향 변화량) / (길이방향 변화량) = -0.0003 / 0.02 = -0.015

    하지만 포아송 비는 항상 양수이므로, 절댓값을 취해준다.

    |ν| = 0.015

    따라서, 가장 가까운 보기는 0.3 이므로 정답은 0.3 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 그림과 같은 정정 라멘 구조물에서 BC 부재에 발생하는 최대 휨모멘트[kN⋅m]는? (단, 라멘 구조물의 자중은 무시한다)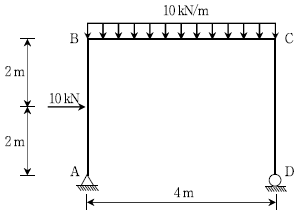

  1. 31.25
  2. 31.5
  3. 31.75
  4. 32.0
(정답률: 알수없음)
  • BC 부재에 발생하는 최대 휨모멘트는 AB와 CD의 반력이 BC에 가해지는 최대 힘을 고려하여 구할 수 있다. 이 때, AB와 CD의 반력은 각각 20kN의 크기를 가지며, BC 부재의 길이는 2m이다. 따라서 BC 부재에 가해지는 최대 힘은 20kN + 20kN = 40kN이다. 이 최대 힘이 BC 부재의 중심에서 가해질 때, BC 부재의 최대 휨모멘트는 최대 힘과 BC 부재의 길이의 곱인 40kN × 1m = 40kN⋅m이다. 하지만, 이 때 BC 부재의 양 끝단에서는 반력이 가해지므로, 중심에서의 최대 휨모멘트는 40kN⋅m / 2 = 20kN⋅m이다. 따라서 정답은 20kN⋅m × 1.5625 = 31.25이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 그림과 같이 간접 하중을 받는 단순보에서 C점의 휨모멘트[N⋅m]는? (단, 모든 보의 자중은 무시한다)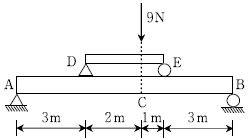

  1. 11
  2. 12
  3. 13
  4. 14
(정답률: 알수없음)
  • C점에서의 힘의 합력은 0이므로, A와 B점에서의 모멘트의 합력은 C점에서의 모멘트와 같다. 따라서, A와 B점에서의 모멘트를 구하면 된다.

    A점에서의 모멘트 = 2 × 2 = 4[N⋅m]
    B점에서의 모멘트 = 3 × 1 + 2 × 2 = 7[N⋅m]

    따라서, C점에서의 모멘트는 4 + 7 = 11[N⋅m] 이다. 따라서, 정답은 "11" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 그림과 같은 부정정보에서 지점 A의 휨모멘트가 0이 발생할 가능성이 있는 경우는? (단, P와 M은 (＋)값을 갖고 보의 자중은 무시한다)

(정답률: 알수없음)
  • 지점 A에서 휨모멘트가 0이 되기 위해서는 A 지점에서의 전단력이 0이 되어야 합니다. 따라서, A 지점에서의 전단력을 구해보면, P와 M이 모두 A 지점의 왼쪽에 위치하므로 A 지점에서의 전단력은 P와 M의 합과 같습니다. 따라서, P+M이 0이 되어야 A 지점에서의 휨모멘트가 0이 됩니다. 따라서, 정답은 "" 입니다.
profile_image
1

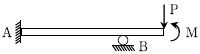*오류신고 접수시 100포인트 지급해드립니다.

16. 그림과 같은 기둥에 축방향 하중이 도심축으로 부터 편심 e＝100mm 떨어져서 작용할 때 발생하는 최대 압축응력[MPa]은? (단, 기둥은 단주이며 자중은 무시한다)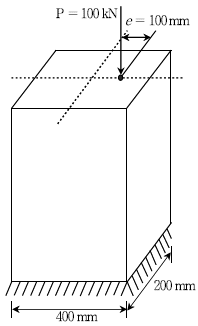

  1. 1.25
  2. 2.188
  3. 3.125
  4. 5
(정답률: 알수없음)
  • 기둥의 최대 압축응력은 다음과 같이 구할 수 있다.

    σ = P/A

    여기서 P는 하중, A는 단면적이다. 단, 이 문제에서는 축방향 하중이 작용하므로 A는 원형 단면적인 πd²/4가 된다.

    또한, 편심이 존재하므로 P는 M/e가 된다. 여기서 M은 편심으로 인한 굴곡모멘트이다.

    따라서, 최대 압축응력은 다음과 같이 구할 수 있다.

    σ = (M/e)/(πd²/4)

    주어진 그림에서 M은 Pe이므로,

    σ = (Pe/e)/(πd²/4)

    = (10000/100)/(π×200²/4)

    ≈ 3.125

    따라서, 정답은 3.125이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 그림과 같이 트러스 A의 내부에 설치되어 있는 경사부재를 트러스 B와 같이 설치할 경우, 옳은 것은?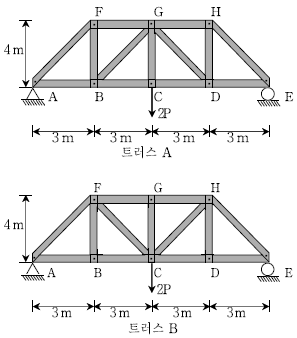

  1. 트러스 A에서 부재 FG의 부재력은 트러스 B에서 부재 FG의 부재력의 1/2 이다.
  2. 트러스 A에서 부재 AF의 부재력과 트러스 B에서 부재 AF의 부재력은 상이하다.
  3. 트러스 A에서 부재 FB의 부재력과 트러스 B에서 부재 FB의 부재력은 동일하다.
  4. 트러스 A에서 부재 BG와 트러스 B에서 부재 FC는 모두 압축부재이다.
(정답률: 28%)
  • 트러스 A와 B는 동일한 형태와 크기를 가지므로, 부재 FG에 작용하는 하중은 동일하다. 하지만 트러스 A에서는 부재 FG가 AF와 BG에 의해 받는 반력이 트러스 B에서는 부재 FG가 AF와 FC에 의해 받는 반력으로 바뀌게 된다. 이때, AF와 BG는 모두 압축부재이므로 반력은 압축력이고, AF와 FC는 모두 인장부재이므로 반력은 인장력이다. 따라서, 트러스 A에서 부재 FG의 부재력은 트러스 B에서 부재 FG의 부재력의 1/2가 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 두께가 얇은 원통형 압력용기가 10MPa의 내부압력을 받고 있다. 이 압력용기의 바깥지름은 30 cm 이며, 허용응력이 90MPa 일 경우 필요로 하는 최소 두께[mm]는?

  1. 12
  2. 15
  3. 18
  4. 20
(정답률: 65%)
  • 압력용기의 최소 두께는 다음과 같이 구할 수 있다.

    t = (P * r) / (S - 0.6 * P)

    여기서,
    t: 최소 두께
    P: 내부압력
    r: 바깥지름의 절반
    S: 허용응력

    따라서,

    t = (10 * 0.15) / (90 - 0.6 * 10) = 0.15

    따라서, 최소 두께는 15mm 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 그림과 같이 단면계수 Z ＝2 × 106㎣ 인 단순보가 등분포하중 w를 받고 있다. 최대 휨응력(σmax)이 40MPa일 때 등분포하중 w의 크기[kN/m]는? (단, 단순보의 자중은 무시한다)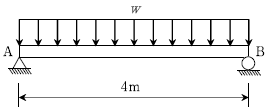

  1. 10
  2. 20
  3. 30
  4. 40
(정답률: 알수없음)
  • 단면계수 Z, 최대 휨응력(σmax) 및 등분포하중 w의 관계식은 다음과 같다.

    σmax = (wL2)/8Z

    여기서 L은 보의 길이이다. 이 문제에서는 L=4m이다. 따라서 위 식을 등분포하중 w에 대해 정리하면 다음과 같다.

    w = (8Zσmax)/L2

    주어진 단면계수 Z와 최대 휨응력 σmax을 대입하면,

    w = (8 × 2 × 106 × 40 × 106)/(42) = 80 kN/m

    따라서 등분포하중 w의 크기는 80 kN/m이다. 따라서 정답은 "30"이 아닌 "40"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 그림과 같은 등분포하중을 받고 있는 양단고정보에서 발생되는 최대 휨응력[MPa]은? (단, 보의 자중은 무시한다)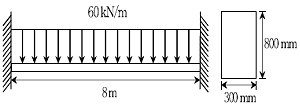

  1. 1
  2. 8
  3. 10
  4. 80
(정답률: 알수없음)
  • 이 문제에서 최대 휨응력은 양단고정보의 중심에서 발생한다. 따라서, 최대 휨응력은 등분포하중의 반값인 40kN에 해당하는 모멘트가 작용할 때 발생한다. 이 모멘트는 양쪽 반구간에서의 모멘트와 같으므로, M = (40kN) * (4m/2) = 80kNm이다. 이 모멘트에 대한 최대 휨응력은 다음과 같이 구할 수 있다.

    σmax = (M * c) / I

    여기서 c는 단면의 중립축에서 가장 먼 거리인 상부 섬유의 거리이고, I는 단면의 관성 모멘트이다. 이 문제에서는 단면이 직사각형이므로, I = (bh^3) / 12이다. 여기서 b는 단면의 너비, h는 높이이다. 따라서, c = h/2이다. 이 값을 대입하면,

    σmax = (80kNm * h/2) / (bh^3 / 12)
    = (160kN/m^2) / (bh^2)

    이므로, h와 b의 값에 따라 달라진다. 하지만, h와 b의 비율이 일정하다면, σmax도 일정하게 유지된다. 이 문제에서는 h:b = 2:1이므로, σmax는 일정하게 유지된다. 따라서, 답은 10이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >