1과목: 과목 구분 없음
1. 다음 그림에서 보의 중앙점 C의 휨모멘트의 크기는? (단, 보의 자중은 무시한다)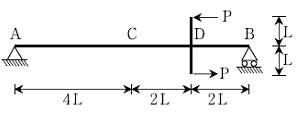
- PL/4
- PL/2
- PL
- 2PL
2. 다음 그림은 집중하중과 등분포하중이 작용하는 단순보의 전단력도(S.F.D.)이다. 이 경우의 최대 휨모멘트의 크기[kN⋅m]는?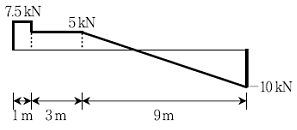
- 22.5
- 30.0
- 45.0
- 60.0
3. 다음 그림과 같이 단면적이 100 mm2인 직사각형 단면의 봉에 인장력 10 kN이 작용할 때, θ=30° 경사면 m-n에 발생하는 수직응력(σ)과 전단응력(τ)의 크기[MPa]는?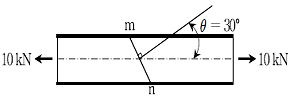
- σ : 25√3, |τ| : 25
- σ : 25√3, |τ| : 25√3
- σ : 75, |τ| : 25
- σ : 75, |τ| : 25√3
4. 다음 그림과 같이 배치된 H형 거더에서 H형 단면의 높이(h)는 500 mm이고, 단면2차모멘트는 2.0 × 108 mm4이며, 항복강도는 250MPa이다. 단면의 항복모멘트(My)의 크기[kN⋅m]는?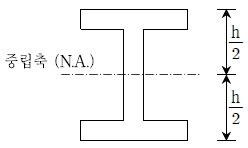
- 100
- 150
- 175
- 200
5. 다음 그림과 같은 구조물 가, 나, 다, 라 중 정정 구조물로만 묶인 것은?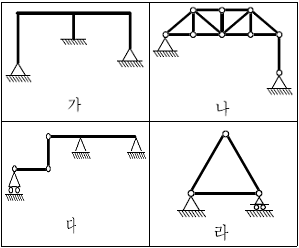
- 나, 다
- 나, 라
- 가, 다, 라
- 나, 다, 라
6. 다음 그림과 같이 힘이 작용하는 구조물에서 부재 AB와 BC에 걸리는 부재력[kN] FAB, FBC는? (단, 부재의 자중과 도르래의 마찰은 무시한다)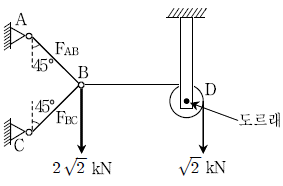
- FAB : 1(인장), FBC : 1(압축)
- FAB : 1(압축), FBC : 1(인장)
- FAB : 3(인장), FBC : 1(압축)
- FAB : 3(압축), FBC : 1(인장)
7. 다음 그림과 같이 구조물에 하중이 작용하며 로울러지점 반력 R이 300 kN이고, 구조물은 평형상태이다. 미지의 힘[kN] F1과 F2는? (단, 구조물의 자중은 무시한다)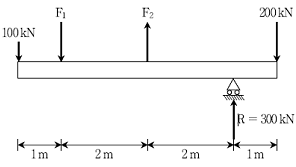
- F1 : 100(상향), F2 : 100(하향)
- F1 : 100(하향), F2 : 100(상향)
- F1 : 150(상향), F2 : 150(하향)
- F1 : 150(하향), F2 : 150(상향)
8. 다음 그림과 같은 기둥 부재에 하중이 작용하고 있다. 부재 AB의 총 수직방향 길이 변화량(δ)은? (단, 단면적 A와 탄성계수 E는 일정하고, 부재의 자중은 무시한다)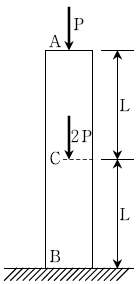
- PL/EA
- 2PL/EA
- 3PL/EA
- 4PL/EA
9. 다음 그림과 같이 강체(rigid body)에 우력이 작용하고 있다. A, B, C점에 관한 모멘트가 각각 ΣMA, ΣMB, ΣMC일 때, 옳은 것은?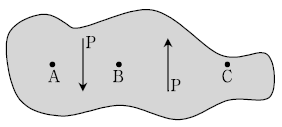
- ΣMA=ΣMB<ΣMC
- ΣMA=ΣMB>ΣMC
- ΣMA<ΣMB<ΣMC
- ΣMA=ΣMB=ΣMC
10. 다음 그림과 같은 트러스에서 부재 BC의 부재력[kN]은?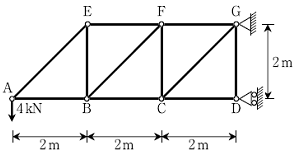
- 8(압축력)
- 8(인장력)
- 16(압축력)
- 16(인장력)
11. 다음 그림과 같이 부재 BDE는 강체(rigid body)이고 D점에서 핀으로 지지되어 있으며, B점에서 수직부재 ABC와 핀으로 연결되어 있다. 이에 대한 설명으로 옳지 않은 것은? (단, 부재 ABC의 단면적 및 탄성계수는 일정하고, 자중은 무시한다)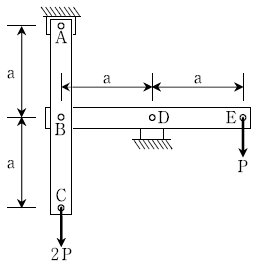
- 위 구조물은 정정구조물이다.
- A 지점의 수직 반력은 위로 P가 작용한다.
- E점은 아래쪽으로 이동한다.
- 수직부재에서 BC 구간의 길이 변화량은 AB 구간의 2배이다.
12. 다음 그림과 같은 내민 보에 등분포 활하중 10 kN/m이 이동하중으로 작용할 때, B점에서의 절대 최대전단력의 크기[kN]는? (단, 보의 자중은 무시한다)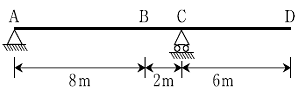
- 48
- 50
- 52
- 68
13. 다음 그림과 같이 중앙 내부힌지 B점에 강성(stiffness) k인 회전스프링에 의하여 지지되는 기둥이 있다. 이 기둥의 임계좌굴하중(Pcr)은?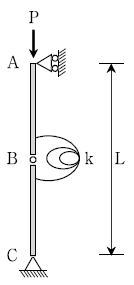
- k/2L
- k/L
- 2k/L
- 4k/L
14. 다음 그림에서 봉 ABC는 강체(rigid body)이고, 현 BD의 축강성 k=20,000 kN/m이다. 이때 C점의 처짐량[mm]은? (단, 부재의 자중은 무시한다)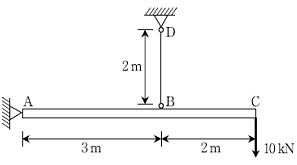
- 20/20
- 25/20
- 20/18
- 25/18
15. 다음 보의 내부힌지 B점에서의 처짐[mm]은? (단, 탄성계수 E=200 GPa, 단면2차모멘트 I=5 × 108 mm4이고, 보의 자중은 무시한다)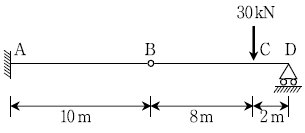
- 10
- 20
- 30
- 40
16. 정육면체에 1축 응력이 작용할 때, 체적 변형률(εv=△V/V)과 포아송비(ν)의 관계로 가장 적합한 것은? (단, 변형은 미소변형이고, 재료는 등방성이며, ε은 변형률, E는 탄성계수이다)
- εv = E/[2(1+ν)]
- εv = (1-2ν)E
- εv = (1-2ν)ε
- εv = ε/[2(1+ν)]
17. 다음 그림과 같이 보의 좌측에는 강성 k1=100 kN/m인 스프링에 의해 지지되며, 우측은 강성이 k2인 2개의 직렬연결된 스프링으로 지지되어 있다. 집중하중 12 kN이 그림과 같이 작용될 때, 양 지점의 처짐량이 같아지기 위한 스프링 강성 k2의 값[kN/m]은? (단, 보와 스프링의 자중은 무시한다)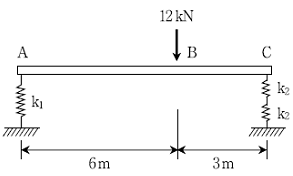
- 100
- 200
- 300
- 400
18. 그림과 같이 수평, 수직 길이가 2L 및 L인 판에 수평방향으로 σ의 응력을 가하였다. 이 경우 포아송 효과에 의해 판의 수직방향 길이는 감소하게 된다. 그 감소한 길이 δ1을 구하고, 동일한 판에서 δ1만큼의 수직방향길이를 증가시키기 위해 가해야 하는 수직방향의 인장응력 σ1은? (단, 재료는 등방성이며, 포아송비는 ν이고, 수평방향의 변형률은 ε이다)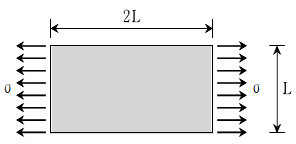
- δ1 : νεL, σ1 : νσ
- δ1 : 2νεL, σ1 : νσ
- δ1 : νεL, σ1 : (1/2)νσ
- δ1 : 2νεL, σ1 : (1/2)νσ
19. 다음 그림에서 두 재료 A, B의 열팽창계수는 αA, αB이며, αA=2αB이다. 온도변화에 의해 발생한 온도응력을 각각 σA, σB라 하면 두 재료의 온도응력의 관계는? (단, 두 재료의 단면적과 탄성계수는 서로 같다)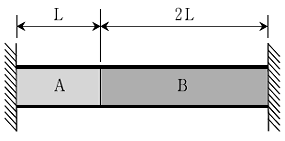
- σA=σB
- σA=-σB
- σA=2σB
- 2σA=-σB
20. 다음 그림과 같이 자중이 20 kN/m인 콘크리트 기초구조에 집중하중 100 kN과 상향으로 등분포 수직토압이 작용할 때, 기초중앙부 C점에 발생하는 모멘트[kN⋅m]는?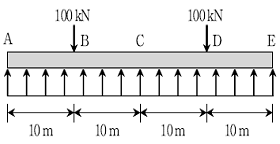
- 1,000(부모멘트)
- 0
- 1,000(정모멘트)
- 2,000(정모멘트)





