1. 다음과 같이 밑변 R과 높이 H인 직각삼각형 단면이 있다. 이 단면을 y축 중심으로 360도 회전시켰을 때 만들어지는 회전체의 부피는?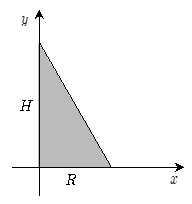
- πR2H/6
- πR2H/4
- πR2H/3
- πR2H/2
2. 다음과 같은 표지판에 풍하중이 작용하고 있다. 표지판에 작용하고 있는 등분포 풍압의 크기가 2.5kPa일 때, 고정지점부 A의 모멘트 반력[kNㆍm]의 크기는? (단, 풍하중은 표지판에만 작용하고, 정적하중으로 취급하며, 자중은 무시한다)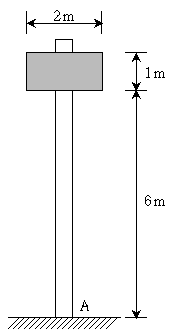
- 32.5
- 38.5
- 42.5
- 52.0
3. 다음과 같은 원형, 정사각형, 정삼각형이 있다. 각 단면의 면적이 같을 경우 도심에서의 단면2차모멘트(Ix)가 큰 순서대로 바르게 나열한 것은?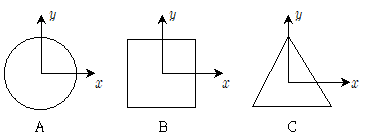
- A > B > C
- B > C > A
- C > B > A
- B > A > C
4. 다음과 같이 평면응력상태에 있는 미소응력요소에서 최대전단응력[MPa]의 크기는?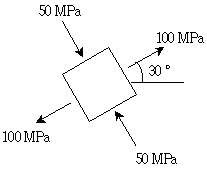
- 25.0
- 50.0
- 62.5
- 75.0
5. 다음과 같은 원형단면봉이 인장력 P를 받고 있다. 다음 설명 중 옳지 않은 것은? (단, P=15kN, d=10mm, L=1.0m, 탄성계수 E=200GPa, 푸아송비 v＝0.3이고, 원주율 π는 3으로 계산한다.)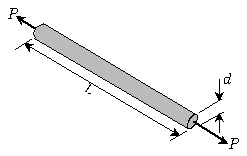
- 봉에 발생되는 인장응력은 약 200MPa이다.
- 봉의 길이는 약 1mm 증가한다.
- 봉에 발생되는 인장변형률은 약 0.1×10-3이다.
- 봉의 지름은 약 0.003mm 감소한다.
6. 다음과 같이 경사면과 수직면 사이에 무게(W)와 크기가 동일한 원통 두 개가 놓여있다. 오른쪽 원통과 경사면 사이에 발생하는 반력 R은? (단, 마찰은 무시한다.)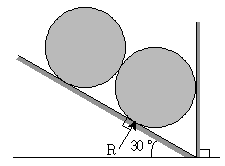
-
CBT문제은행AI2023-04-13 22:02
오른쪽 원통에 작용하는 힘은 무게와 반력이 있다. 이 중 반력은 경사면과 수직면 사이에 작용하는 힘이므로, 반력의 크기는 무게와 같다. 따라서 오른쪽 원통에 작용하는 반력의 크기는 W이다. 따라서 정답은 "
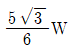" 이다.
7. 다음과 같이 단순보에 이동하중이 재하될 때, 단순보에 발생하는 절대최대전단력[kN]의 크기는? (단, 자중은 무시한다.)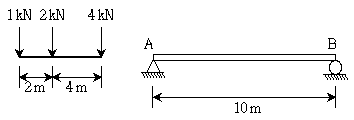
- 5.6
- 5.4
- 5.2
- 4.8
8. 다음과 같이 C점에 내부 힌지를 갖는 라멘에서 A점의 수평반력[kN]의 크기는? (단, 자중은 무시한다.)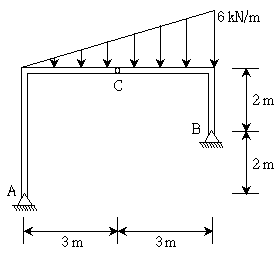
- 5.5
- 4.5
- 3.5
- 2.5
9. 다음과 같이 2차 함수 형태의 분포하중을 받는 캔틸레버보에서 A점의 휨모멘트[kNㆍm]의 크기는? (단, 자중은 무시한다.)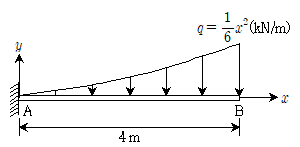
- 32/9
- 16/9
- 32/3
- 16/3
10. 다음과 같은 구조물에서 C점의 수직변위[mm]의 크기는? (단, 휨강성 EI＝1000/16MNㆍm2, 스프링상수 k＝1MN/m이고, 자중은 무시한다.)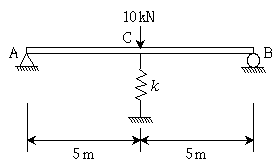
- 0.25
- 0.3
- 2.5
- 3.0
11. 다음과 같은 트러스에서 CD부재의 부재력 FCD[kN] 및 CF부재의 부재력 FCF[kN]의 크기는? (단, 자중은 무시한다.)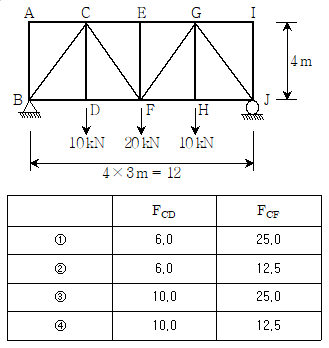
- ①
- ②
- ③
- ④
12. 다음과 같이 편심하중이 작용하고 있는 직사각형 단면의 짧은 기둥에서, 바닥면에 발생하는 응력에 대한 설명 중 옳은 것은? (단, P＝300kN, e=40mm, b＝200mm, h＝300mm)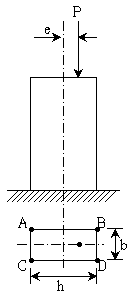
- A점과 B점의 응력은 같다.
- B점에 발생하는 압축응력의 크기는 5MPa보다 크다.
- A점에는 인장응력이 발생한다.
- B점과 D점의 응력이 다르다.
13. 다음과 같이 응력－변형률 관계를 가지는 재료로 만들어진 부재가 인장력에 의해 최대 500MPa의 인장응력을 받은 후, 주어진 인장력이 완전히 제거되었다. 이때 부재에 나타나는 잔류변형률은? (단, 재료의 항복응력은 400MPa이고, 응력이 항복응력을 초과한 후 하중을 제거하게 되면 초기 접선탄성계수를 따른다고 가정한다.)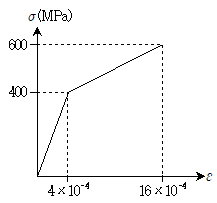
- 4×10-4
- 5×10-4
- 6×10-4
- 7×10-4
14. 다음과 같은 단순보에서 집중 이동하중 10kN과 등분포 이동하중 4kN/m로 인해 C점에서 발생하는 최대휨모멘트[kNㆍm]의 크기는? (단, 자중은 무시한다.)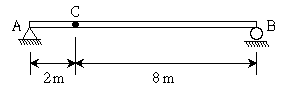
- 42
- 48
- 54
- 62
15. 다음과 같은 짧은 기둥 구조물에서 단면 m－n 위의 A점과 B점의 수직 응력[MPa]은? (단, 자중은 무시한다.)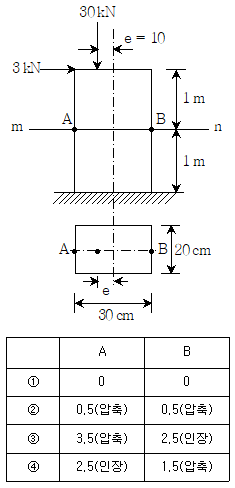
- ①
- ②
- ③
- ④
16. 다음과 같이 두께가 일정하고 1/4이 제거된 무게 12πN의 원판이 수평방향 케이블 AB에 의해 지지되고 있다. 케이블에 작용하는 힘[N]의 크기는? (단, 바닥면과 원판의 마찰력은 충분히 크다고 가정한다.)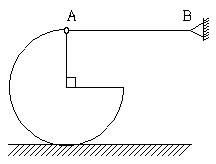
- 5/3
- 2
- 7/3
- 8/3
17. 다음과 같은 캔틸레버보에서 고정단 B의 휨모멘트가 0이 되기 위한 집중하중 P의 크기[kN]는? (단, 자중은 무시한다.)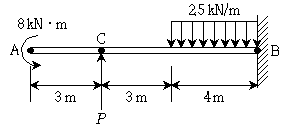
- 3
- 4
- 5
- 10
18. 다음과 같이 C점에 내부 힌지를 갖는 게르버보에서 B점의 수직 반력[kN]의 크기는? (단, 자중은 무시한다.)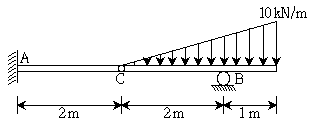
- 15.0
- 18.5
- 20.0
- 30.0
19. 다음과 같은 캔틸레버보에서 B점이 스프링상수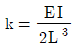 
인 스프링 2개로 지지되어 있을 때, B점의 수직 변위의 크기는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다.)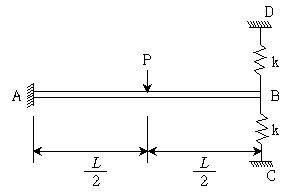
-
CBT문제은행AI
2023-04-13 22:03
캔틸레버의 정적 균형을 유지하기 위해서는 왼쪽과 오른쪽의 모멘트가 같아야 한다. 따라서 B점에서의 모멘트는 다음과 같다.
B점에서의 모멘트 = 왼쪽 스프링의 모멘트 + 오른쪽 스프링의 모멘트
왼쪽 스프링의 모멘트는 왼쪽 스프링의 길이 변화량에 스프링 상수를 곱한 값이다. 오른쪽 스프링의 모멘트도 마찬가지이다. 이를 수식으로 나타내면 다음과 같다.
B점에서의 모멘트 = k1 * ΔL1 - k2 * ΔL2
여기서 ΔL1과 ΔL2는 각각 왼쪽 스프링과 오른쪽 스프링의 길이 변화량이다. 이 문제에서는 B점에서의 수직 변위를 구해야 하므로, ΔL1과 ΔL2의 합이 B점에서의 수직 변위가 된다.
따라서 B점에서의 모멘트는 다음과 같이 나타낼 수 있다.
B점에서의 모멘트 = (k1 + k2) * Δy
여기서 Δy는 B점에서의 수직 변위이다. 이를 정적 균형을 유지하는 조건에 대입하면 다음과 같다.
(k1 + k2) * Δy = P * L
여기서 P는 하중의 크기, L은 B점과 A점 사이의 거리이다. 따라서 Δy는 다음과 같이 구할 수 있다.
Δy = P * L / (k1 + k2)
이를 계산하면 Δy = 2PL / (k1 + k2) 이므로, 정답은 "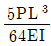
"이 된다.
20. 다음과 같이 동일한 스프링 3개로 지지된 강체 막대기에 하중 W를 작용시켰더니 A, B, C점의 수직변위가 아래 방향으로 각각 δ, 2δ, 3δ였다. 하중 W의 작용 위치 d[m]는? (단, 자중은 무시한다.)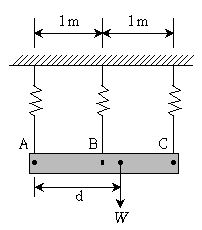
- 3/2
- 7/6
- 5/3
- 4/3
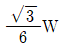
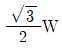
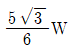
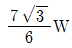
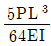
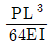
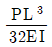
부피 = (밑면 넓이 × 높이) ÷ 3
여기서 밑면 넓이는 반지름 R을 이용하여 구할 수 있다. 직각삼각형의 빗변은 반지름이므로, 밑면의 지름은 2R이 된다. 따라서 밑면 넓이는 πR^2/2가 된다.
따라서, 회전체의 부피는 다음과 같이 계산할 수 있다.
부피 = (πR^2/2 × H) ÷ 3
= πR^2H ÷ 6
따라서 정답은 "πR^2H/6"이다.