1. 그림과 같이 단부 경계 조건이 각각 다른 장주에 대한 탄성 좌굴하중(Pcr)이 가장 큰 것은? (단, 기둥의 휨강성 EI＝4000kNㆍm2이며, 자중은 무시한다)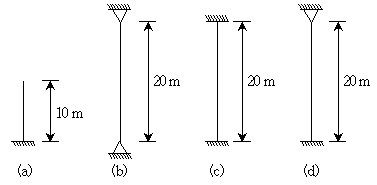
- (a)
- (b)
- (c)
- (d)
2. 그림과 같이 2개의 힘이 동일점 O에 작용할 때 합력(R)의 크기[kN]와 방향(α)은? (순서대로 R, α)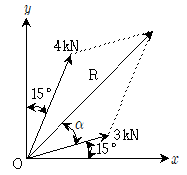
- √37,
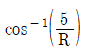
- √37,
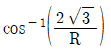
- √61,
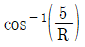
- √61,
-
CBT문제은행AI2023-04-13 22:03
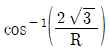
먼저, 두 힘이 작용하는 방향을 이루는 각도를 구해야 한다. 이를 구하기 위해 삼각형의 코사인 법칙을 이용한다.
cosα = (3² + 4² - 5²) / (2 × 3 × 4) = 0.2
α = cos⁻¹(0.2) ≈ 78.46°
이제 합력의 크기를 구하기 위해 두 힘의 x, y 성분을 구한다.
Fx = 3 + 4cosα ≈ 6.8
Fy = 4sinα ≈ 3.1
따라서 합력 R은 √(Fx² + Fy²) ≈ √37 이다. 또한, 합력의 방향은 arctan(Fy/Fx) ≈ 26.57° 이므로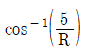
이다.
3. 그림과 같이 직사각형 단면을 갖는 단주에 집중하중 P＝120kN이 C점에 작용할 때 직사각형 단면에서 인장응력이 발생하는 구역의 넓이[m2]는?
- 2
- 3
- 4
- 5
4. 그림과 같은 트러스에서 부재 CG에 대한 설명으로 옳은 것은? (단, 모든 부재의 자중은 무시한다)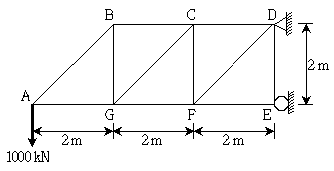
- 압축 부재이다.
- 부재력은 2000kN이다.
- 부재력은 1000kN이다.
- 부재력은 1000√2kN이다.
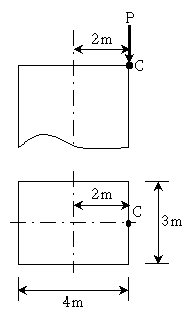
5. 그림과 같은 외팔보에서 B점의 회전각은? (단, 보의 휨강성 EI는 일정하며, 자중은 무시한다)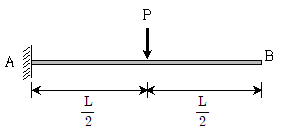
-
CBT문제은행AI
2023-04-13 22:03
외팔보에서 B점은 고정점이 아니므로 회전운동을 한다. 이 때, 회전운동을 하는 물체에 작용하는 힘은 중심축을 중심으로 회전운동을 하는 모멘트를 만들어내는 힘이다. 따라서, B점에서의 회전각은 모멘트의 크기와 보의 휨강성 EI, 보의 길이 L에 따라 결정된다. 이 문제에서는 보의 휨강성 EI와 길이 L이 일정하므로, 모멘트의 크기가 가장 큰 경우가 B점에서의 회전각이 가장 크다. 모멘트의 크기는 A점에서의 하중과 A-B 사이의 거리인 2m의 곱으로 계산할 수 있다. 따라서, B점에서의 회전각은 2mL/EI가 된다. 따라서, 정답은 "
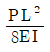"이다.
6. 그림과 같은 단순보에서 절대 최대 휨모멘트의 크기[kNㆍm]는? (단, 보의 휨강성 EI는 일정하며, 자중은 무시한다)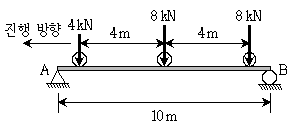
- 23.32
- 26.32
- 29.32
- 32.32
7. 그림과 같이 빗금 친 단면의 도심을 G라 할 때, x축에서 도심까지 거리(y)는?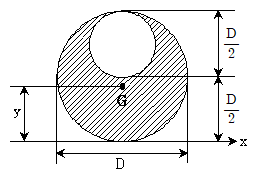
-
CBT문제은행AI
2023-04-13 22:02
단면의 도심 G는 도형의 중심이므로, 단면의 넓이를 2로 나눈 값인 12/2=6이 x축에서 도심까지의 거리(y)가 됩니다. 따라서 정답은 "
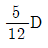"입니다.
8. 한 점에서의 미소 요소가 εx＝300×10-6, εy＝100×10－6, γxy＝－200×10－6인 평면 변형률을 받을 때, 이 점에서 주 변형률의 방향(θP)은? (단, 방향의 기준은 x축이며, 반시계 방향을 양의 회전으로 한다)
- 22.5°, 112.5°
- 45°, 135°
- －22.5°, 67.5°
- －45°, 45°
9. 그림과 같은 단순보에서 B점에 집중하중 P＝10kN이 연직 방향으로 작용할 때 C점에서의 전단력 Vc[kN] 및 휨모멘트 Mc[kNㆍm]의 값은? (단, 보의 휨강성 는 일정하며, 자중은 무시한다) (순서대로 Vc, Mc)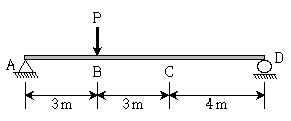
- －3, 10
- －3, 12
- －7, 14
- －7, 16
10. 그림과 같이 양단 고정된 보에 축력이 작용할 때 지점 B에서 발생하는 수평 반력의 크기[kN]는? (단, 보의 축강성 EA는 일정하며, 자중은 무시한다)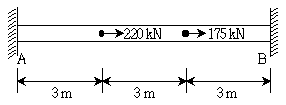
- 190
- 200
- 210
- 220
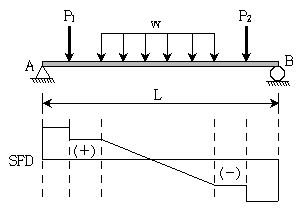
11. 그림과 같이 단순보에 작용하는 여러 가지 하중에 대한 전단력도(SFD)로 옳지 않은 것은? (단, 보의 자중은 무시한다)
-
CBT문제은행AI
2023-04-13 22:02
옳지 않은 것은 "
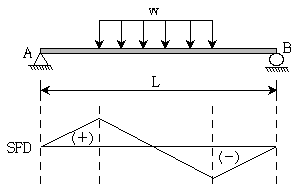"이다. 이유는 SFD는 하중의 크기와 위치에 따라 변화하며, 하중이 왼쪽에서 오른쪽으로 증가할 때는 SFD가 감소하고, 하중이 오른쪽에서 왼쪽으로 증가할 때는 SFD가 증가한다. 따라서, ""는 하중이 오른쪽에서 왼쪽으로 증가하는데, SFD가 감소하고 있으므로 옳지 않다.
12. 그림과 같은 보 ABC에서 지점 A에 수직 반력이 생기지 않도록 하기 위한 수직 하중 P의 값[kN]은? (단, 모든 구조물의 자중은 무시한다)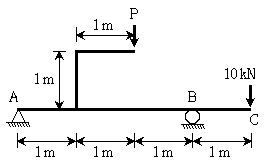
- 5
- 10
- 15
- 20
13. 폭 0.2m, 높이 0.6m의 직사각형 단면을 갖는 지간 L＝2m 단순보의 허용 휨응력이 40MPa일 때 이 단순보의 중앙에 작용시킬 수 있는 최대 집중하중 P의 값[kN]은? (단, 보의 휨강성 EI는 일정하며, 자중은 무시한다)
- 240
- 480
- 960
- 1080
14. 그림과 같이 일정한 두께 t＝10mm의 직사각형 단면을 갖는 튜브가 비틀림 모멘트 T＝300kNㆍm를 받을 때 발생하는 전단흐름의 크기[kN/m]는?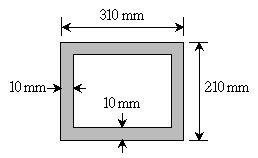
- 0.25
- 2500
- 5000
- 0.5
15. 그림과 같이 단순보 중앙 C점에 집중하중 P가 작용할 때 C점의 처짐에 대한 설명으로 옳은 것은? (단, 보의 자중은 무시한다)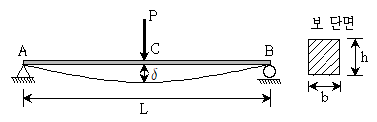
- 집중하중 P를 P/2로 하면 처짐량 δ는 δ/4가 된다.
- 부재의 높이 h를 그대로 두고 폭 b를 2배로 하면 처짐량 δ는 δ/4가 된다.
- AB 간의 거리 L을 L/2로 하면 처짐량 δ는 가 δ/6된다.
- 부재의 폭 b를 그대로 두고 높이 h를 2배로 하면 처짐량 δ는 δ/8가 된다.
16. 그림과 같은 라멘 구조물에 수평 하중 P＝12kN이 작용할 때 지점 B의 수평 반력 크기[kN]와 방향은? (단, 자중은 무시하며, E점은 내부 힌지이다)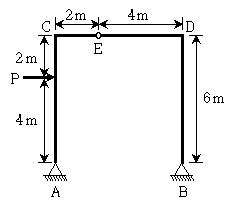
- 14/3(←)
- 16/3(←)
- 18/3(→)
- 20/3(←)
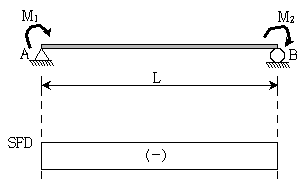
17. 그림과 같은 단순보에 모멘트 하중이 작용할 때 발생하는 지점 A의 수직 반력(RA)과 지점 B의 수직 반력(RB)의 크기[kN]와 방향은? (단, 보의 휨강성 EI는 일정하며, 자중은 무시한다) (순서대로 RA, RB)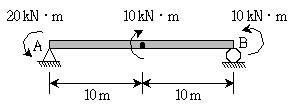
- 1(↑), 1(↓)
- 1(↓), 1(↑)
- 2(↑), 2(↓)
- 2(↓), 2(↑)
18. 그림과 같은 부정정보에 등분포하중 w=10kN/m가 작용할 때, 지점 A에 발생하는 휨모멘트 값[kNㆍm]은? (단, 보의 휨강성 EI는 일정하며, 자중은 무시한다)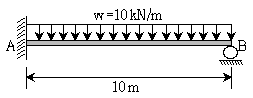
- －125
- －135
- －145
- －155
19. 그림과 같은 2개의 게르버보에 하중이 각각 작용하고 있다. 그림(a)에서 지점 A의 수직 반력(RA)과 그림(b)에서 지점 D의 수직 반력(RD)이 같기 위한 하중 P의 값[kN]은? (단, 보의 자중은 무시한다)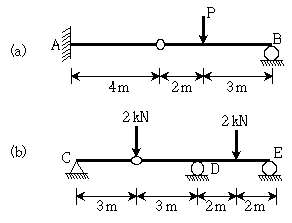
- 4.5
- 5.5
- 6.5
- 7.5
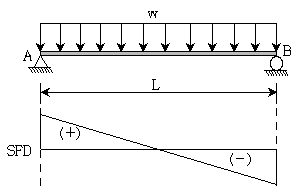
20. 다음 그림은 단순보에 수직 등분포하중이 일부 구간에 작용했을 때의 전단력도이다. 이 단순보에 작용하는 등분포하중의 크기[kN/m]는? (단, 보의 휨강성 EI는 일정하며, 자중은 무시한다)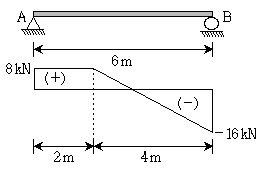
- 4
- 6
- 8
- 12
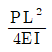
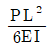
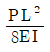
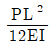
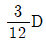
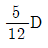
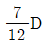
Pcr = (nπ/L)2 EI
여기서 n은 좌굴모드, L은 장주 길이, EI는 휨강성이다.
따라서, 각각의 장주에 대한 Pcr을 구해보면 다음과 같다.
(a) 단순 연속보 - Pcr = (1π/2m)2 × 4000kNㆍm2 = 7853.98kN
(b) 고정단 - Pcr = (1π/2m)2 × 4000kNㆍm2 = 7853.98kN
(c) 자유단 - Pcr = (2π/2m)2 × 4000kNㆍm2 = 31415.93kN
(d) 연속보와 고정단의 결합 - Pcr = (1.5π/2m)2 × 4000kNㆍm2 = 17657.95kN
따라서, 자유단에 대한 Pcr이 가장 크므로 정답은 (c)이다.