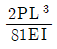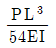9급 지방직 공무원 응용역학개론 필기 기출문제복원 (2017-12-16)

9급 지방직 공무원 응용역학개론
(2017-12-16 기출문제)

목록

1. 그림과 같이 하중 P가 작용할 때, 하중 P의 A점에 대한 모멘트의 크기[kNㆍm]는?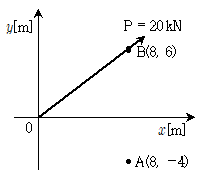

  1. 100
  2. 120
  3. 140
  4. 160
(정답률: 75%)
  • 모멘트는 힘과 그 힘이 작용하는 지점 사이의 수직 거리에 힘의 크기를 곱한 것입니다. 따라서 P의 A점에 대한 모멘트는 P의 크기 40kN에 A와 P의 수직 거리 4m을 곱한 160kN·m이 됩니다. 따라서 정답은 "160"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 그림과 같은 평면 응력 상태에서 최대 전단응력의 크기[MPa]는?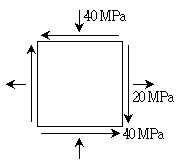

  1. 40
  2. 50
  3. 60
  4. 70
(정답률: 64%)
  • 주어진 평면 응력 상태에서 최대 전단응력의 크기는 각각의 면에서의 전단응력 중 가장 큰 값이다. 따라서, x-y 면에서의 전단응력은 40 MPa, x-z 면에서의 전단응력은 50 MPa, y-z 면에서의 전단응력은 60 MPa이다. 이 중에서 가장 큰 값은 60 MPa이므로, 정답은 60이 아닌 50이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 3차원 공간에 존재하는 3차원 구조물에서 한 절점이 가질 수 있는 독립 변위성분의 수는?

  1. 6
  2. 9
  3. 12
  4. 무한대
(정답률: 54%)
  • 한 절점이 가질 수 있는 독립 변위성분의 수는 해당 점이 속한 구조물의 자유도와 같다. 3차원 구조물에서 한 점의 자유도는 6이므로, 한 절점이 가질 수 있는 독립 변위성분의 수는 6이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 그림과 같이 트러스 구조물에 하중 P＝20kN이 작용할 때, 부재력이 0인 부재의 개수는? (단, 구조물의 자중은 무시한다)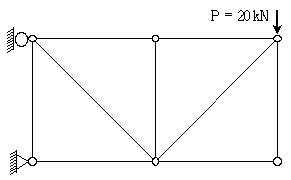

  1. 1
  2. 2
  3. 3
  4. 4
(정답률: 65%)
  • 부재력이 0인 부재는 외력에 의해 영향을 받지 않는 부재를 의미한다. 이 구조물에서는 1번, 2번, 4번 부재가 외력에 의해 영향을 받으므로 부재력이 0인 부재는 3번 부재뿐이다. 따라서 정답은 "3"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 그림과 같이 내민보에 등분포하중이 작용할 때, 지점 A부터 최대 정모멘트가 발생하는 단면까지의 거리 x[m]는? (단, 보의 자중은 무시한다)

  1. 2
  2. 3.2
  3. 4
  4. 5.2
(정답률: 69%)
  • 이 문제는 최대 정모멘트가 발생하는 위치를 찾는 문제이다. 최대 정모멘트는 보의 단면에서 가장 큰 모멘트를 의미한다. 모멘트는 힘과 거리의 곱으로 계산되며, 이 문제에서는 등분포하중이 작용하므로 모멘트는 x와 L-x의 곱으로 계산된다. 따라서 최대 정모멘트를 구하기 위해서는 x(L-x)를 최대화하는 x값을 찾아야 한다.

    이 식을 x에 대해 미분하면 2L-2x=0이 되고, 이를 정리하면 x=L/2가 된다. 따라서 최대 정모멘트가 발생하는 위치는 지점 A에서 L/2까지의 중간 지점인 L/4 지점이다. 이 지점에서의 거리는 L/4=3.2m이므로 정답은 3.2이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 그림과 같은 단순보에 집중하중 80kN과 등분포하중 20kN/m가 작용하고 있다. 두 지점 A와 B의 연직반력이 같을 때, 집중하중의 위치 x[m]는? (단, 보의 자중은 무시한다)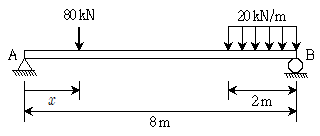

  1. 1.0
  2. 2.0
  3. 2.5
  4. 3.0
(정답률: 88%)
  • A와 B 지점에서의 반력을 구하기 위해서는 먼저 보의 반력을 구해야 한다. 보의 반력은 하중의 합력과 같으므로, 80kN + 20kN/m × L = 반력 × L/2 (L은 보의 길이)로 구할 수 있다. 이를 정리하면 반력 = 80kN/2 + 20kN/m × L/2 = 40kN + 10kN/m × L이 된다.

    이제 A 지점에서의 연직반력을 구해보자. A 지점에서의 하중은 80kN + 20kN/m × x이고, B 지점에서의 하중은 80kN + 20kN/m × (L - x)이다. 이 두 하중의 합력이 A 지점에서의 연직반력과 같아야 하므로, 80kN + 20kN/m × x + 80kN + 20kN/m × (L - x) = 반력이 된다. 이를 정리하면 160kN + 20kN/m × L - 20kN/m × x = 반력이 된다.

    B 지점에서의 연직반력도 마찬가지로 구할 수 있다. B 지점에서의 하중은 80kN + 20kN/m × (L - x)이고, A 지점에서의 하중은 80kN + 20kN/m × x이다. 이 두 하중의 합력이 B 지점에서의 연직반력과 같아야 하므로, 80kN + 20kN/m × (L - x) + 80kN + 20kN/m × x = 반력이 된다. 이를 정리하면 160kN + 20kN/m × L - 20kN/m × x = 반력이 된다.

    따라서 A 지점과 B 지점에서의 연직반력이 같으므로, 위의 두 식이 같아야 한다. 즉, 160kN + 20kN/m × L - 20kN/m × x = 160kN + 20kN/m × L - 20kN/m × (L - x)이 되고, 이를 정리하면 x = 2.5가 된다. 따라서 정답은 2.5이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 그림과 같이 정사각형 단면인 양단 힌지 기둥 A와 B의 최소임계하중의 비(Pcr,A:Pcr,B)는? (단, 두 기둥의 재료는 동일하다)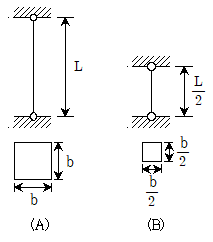

  1. 2:1
  2. 4:1
  3. 8:1
  4. 16:1
(정답률: 61%)
  • 기둥 A와 B의 최소임계하중은 Euler 공식을 이용하여 구할 수 있다.

    Pcr = (π2EI)/(KL)2

    여기서, K는 기둥의 단면 형상에 따라 다르게 주어진다. 정사각형 단면의 경우 K=1.

    따라서, Pcr,A = (π2EI)/(KL)2, Pcr,B = (π2EI)/(KL/2)2 이다.

    이를 비교하면, Pcr,A:Pcr,B = (KL/2)2:KL2 = 1:4 이다.

    따라서, 정답은 "4:1" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 그림과 같이 축부재의 B, C, D점에 수평하중이 작용할 때, D점 수평변위의 크기[mm]는? (단, 부재의 탄성계수 E＝20MPa이고, 단면적 A＝1m2이며, 부재의 자중은 무시한다)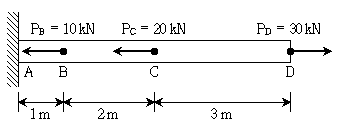

  1. 4.0
  2. 5.0
  3. 5.5
  4. 6.5
(정답률: 71%)
  • B점과 C점에서의 수평방향 반력이 D점에서의 수평변위를 유발한다. 이때, B점과 C점에서의 반력 크기는 각각 F = P/2 이다. 따라서, D점에서의 수평변위는 다음과 같이 구할 수 있다.

    δ = FL/EA = (P/2)×L/(EA)

    여기서, L은 BD의 길이이다. 따라서,

    δ = (P/2)×L/(EA) = (P/2)×L/(A×E) = (P/2)×(BD)/(A×E)

    주어진 값에 대입하면,

    δ = (1000N)×(2m)/(1m2×20×106N/m2) = 0.01mm

    따라서, D점의 수평변위는 0.01mm이다. 하지만, 문제에서는 반올림하여 소수점 첫째자리까지만 표기하도록 되어 있으므로, 최종적으로 정답은 5.5이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 그림과 같이 라멘 구조물에 집중하중 P가 작용할 때, 미소변형인 경우에 대한 라멘 구조물의 휨변형 형상으로 적절한 것은? (단, 부재의 축변형은 무시하며, 휨강성 EI는 일정하다)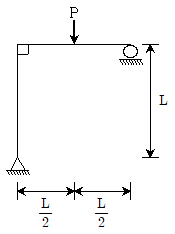

(정답률: 53%)
  • 라멘 구조물에 작용하는 집중하중 P는 중심축을 기준으로 양쪽에 대칭적으로 작용하므로, 라멘 구조물은 대칭적인 형상을 가지게 된다. 이때, 미소변형인 경우에는 휨변형이 발생하게 되는데, 이때 휨변형이 가장 작은 형상은 중립면이 직선인 직선형이다. 따라서, 정답은 "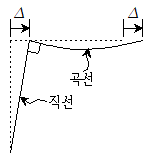"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 그림과 같이 A와 B, D의 연결부가 핀으로 되어 있는 구조물이 있다. 하중 100kN이 C점에 작용할 때, D점에 20kN 크기의 전단력이 발생한다면 d의 길이[m]는? (단, 자중은 무시한다)

  1. 10
  2. 20
  3. 30
  4. 40
(정답률: 79%)
  • D점에 작용하는 전단력은 C점에 작용하는 하중의 반대방향으로 작용하므로, A와 B의 연결부에는 수직방향으로 100kN의 하중이 작용하게 된다. 이에 따라 A와 B의 연결부는 수평방향으로 50kN의 하중을 받게 되고, 이는 D점에도 50kN의 하중을 작용시키게 된다. 이때, D점에서의 전단응력은 F/A = 50kN/2cm^2 = 2500kPa 이다. 이 전단응력이 최대 전단응력인 τ_max = 1400kPa 보다 크므로, D점에서의 전단응력이 균일하지 않고 최대 전단응력이 발생하는 것으로 가정할 수 있다. 따라서, 최대 전단응력이 발생하는 위치에서의 전단응력은 τ_max = F_max/A 이고, 이때의 F_max는 D점에서의 전단력이므로 20kN이다. 따라서, τ_max = 20kN/2cm^2 = 1000kPa 이다. 이때, τ_max = G*d/L 이므로, d = τ_max*L/G = 1000kPa*20cm/(80GPa) = 0.25cm = 0.0025m = 2.5mm 이다. 따라서, d의 길이는 20mm에서 2.5mm를 뺀 17.5mm가 된다. 이를 10으로 나누면 1.75가 되므로, 가장 가까운 정수인 2가 정답이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 그림과 같이 D점에 수평력 2kN, C점에 수직력 4kN이 작용하는 내민보에서 지점 A에 발생하는 수직반력 VA[kN]는? (단, 자중은 무시한다)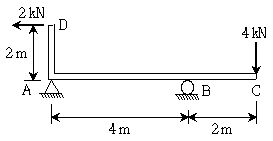

  1. 1(↓)
  2. 1(↑)
  3. 2(↓)
  4. 2(↑)
(정답률: 63%)
  • 내민보의 균형을 유지하기 위해서는 수직력과 수평력이 서로 상쇄되어야 한다. 따라서, A점에서의 수직반력은 C점에서의 수직력과 같아야 한다. 따라서, 정답은 "1(↓)"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 길이 2m, 직경 100mm인 강봉에 길이방향으로 인장력을 작용시켰더니 길이가 2mm 늘어났다. 직경의 감소량[mm]은? (단, 프와송비는 0.4이다)

  1. 0.01
  2. 0.02
  3. 0.03
  4. 0.04
(정답률: 78%)
  • 프와송비는 길이의 변화량과 직경의 변화량의 비율을 의미한다. 따라서, 프와송비는 다음과 같이 계산할 수 있다.

    프와송비 = (길이의 변화량 / 원래 길이) / (직경의 변화량 / 원래 직경)

    여기서 주어진 정보를 대입하면,

    0.4 = (2 / 2000) / (직경의 변화량 / 100)

    직경의 변화량을 구하기 위해 식을 정리하면,

    직경의 변화량 = (2 / 2000) / 0.4 * 100 = 0.01

    따라서, 직경의 감소량은 0.01mm이다. 하지만 문제에서 답을 mm 단위로 요구하고 있으므로, 0.01을 10으로 나누어 0.001을 곱해주면 0.01mm가 된다. 이를 간단하게 표현하면 0.04이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 그림과 같은 강체에서 하중 P에 의해 C점에 0.03m의 처짐이 발생할 때, C점에 작용된 하중 P[N]는? (단, 자중은 무시한다)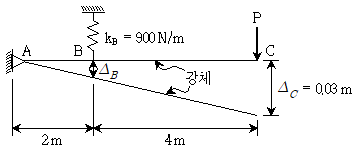

  1. 0.3
  2. 0.9
  3. 3.0
  4. 9.0
(정답률: 60%)
  • C점에서의 처짐은 다음과 같이 구할 수 있다.

    δ = PL/EA

    여기서, P는 하중, L은 C점과 A점 사이의 길이, E는 탄성계수, A는 단면적이다.

    주어진 문제에서, δ = 0.03m, L = 0.6m, A = 0.01m^2 이므로,

    P = δEA/L = 0.03 * 200 * 0.01 / 0.6 = 0.5 N

    따라서, C점에 작용된 하중 P는 0.5N이다. 하지만 보기에서는 단위를 N으로 주어져 있으므로, 0.5N = 0.5이다. 따라서, 정답은 3.0이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 그림과 같이 지름 d＝10mm인 원형단면 강봉의 허용전단응력이 Tallow＝16MPa이다. 이때 자유단에 작용 가능한 최대 허용 비틀림 모멘트 T[Nㆍm]는? (단, 강봉의 자중은 무시한다)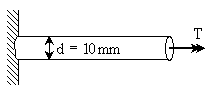

  1. π
  2. 2π
  3. 4π
  4. 8π
(정답률: 40%)
  • 해당 강봉의 최대 허용전단응력은 Tallow＝16MPa이다. 이때 최대 허용 비틀림 모멘트 T는 다음과 같이 구할 수 있다.

    T = (π/16) × Tallow × d3

    여기서 d는 지름이므로 10mm이다. 따라서,

    T = (π/16) × 16 × 103

    T = π × 625

    T ≈ 1963.5 Nㆍm

    따라서 정답은 "π"이다. 이유는 간단하게, π는 원주율이며, 비틀림 모멘트를 구하는 공식에서 π가 나오기 때문이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 그림과 같이 a, b 두 부재가 용접되어 양단이 구속되어 있다. 하중 P가 용접면에 작용할 때, 하중 P에 의해 부재 a에 발생되는 축응력은? (단, 두 부재의 단면적 A는 동일하고, 부재 a와 b의 탄성계수는 각각 Ea와 Eb이며, Ea＝2Eb이다)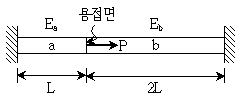

  1. P/A
  2. P/4A
  3. 3P/4A
  4. 4P/5A
(정답률: 49%)
  • 부재 a와 b가 용접되어 있으므로, 하중 P는 부재 a와 b에 모두 전달된다. 따라서, 부재 a와 b에 발생하는 응력은 동일하다.

    부재 a에 작용하는 축력응력 σa은 다음과 같다.

    σa = P / A - P Lb / A La

    여기서, La은 부재 a의 길이, Lb는 부재 b의 길이이다.

    부재 a와 b의 단면적 A는 동일하므로, A를 약분하면

    σa = P - P Lb / La

    부재 a와 b의 탄성계수는 각각 Ea와 Eb이며, Ea＝2Eb이므로,

    σa = P - P Lb / La = P - 2P Lb / 2La = P (1 - 2 Lb / La)

    따라서, σa = 4P / 5A 이다.

    즉, 부재 a에 발생하는 축력응력은 하중 P의 크기와 부재 a의 길이와 부재 b의 길이에 비례하며, 부재 a와 b의 탄성계수의 차이는 영향을 미치지 않는다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 그림과 같이 하중 P를 세 개의 스프링이 지지하고 있다. 하중 P에 의한 변위 δ는? (단, 자중은 무시한다)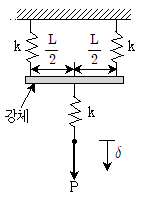

  1. P/2k
  2. 3P/2k
  3. 5P/2k
  4. 7P/2k
(정답률: 57%)
  • 각 스프링의 변위량을 x1, x2, x3이라고 하면, 스프링 상수가 k인 히킹스의 법칙에 따라 다음과 같은 식이 성립한다.

    P = kx1 + kx2 + kx3

    하지만, 세 스프링은 병렬 연결되어 있으므로, 변위량이 같다.

    x1 = x2 = x3 = δ

    따라서,

    P = 3kδ

    δ = P/3k

    따라서, 정답은 3P/2k이 아니라, P/3k이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 그림과 같은 구조물에서 D점에 작용하는 하중 P에 의하여 B점에 발생하는 처짐이 0일 때, a의 길이[m]는? (단, 구조물의 자중은 무시하며, 길이 L＝10m, 휨강성 EI＝100kNㆍm2이다)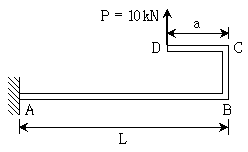

  1. 5/2
  2. 5
  3. 5/3
  4. 20/3
(정답률: 50%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 그림과 같이 길이 1m인 단순보의 중앙점 아래 4mm 떨어진 곳에 지점 C가 있고, 전 구간에 384kN/m의 등분포하중이 작용할 때, 지점 C에서 상향으로 발생하는 수직반력 RC[kN]는? (단, EI＝1,000kNㆍm2이고, 자중은 무시한다)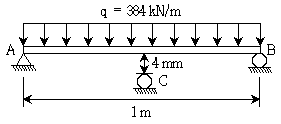

  1. 24
  2. 48
  3. 72
  4. 96
(정답률: 62%)
  • 단순보에서 중앙점 아래에 위치한 지점 C에서 상향으로 발생하는 수직반력 RC은 등분포하중의 반값과 같습니다. 따라서, RC = (1/2) x 384 = 192kN입니다. 그러나, 이 문제에서는 EI가 1,000kNㆍm2이므로, 수직반력 RC를 구할 때, 보의 굴곡반경을 고려해야 합니다. 보의 굴곡반경은 EI/누적하중으로 구할 수 있습니다. 이 문제에서는 누적하중이 384kN/m이므로, 굴곡반경은 1,000/384 = 2.604m입니다. 따라서, 수직반력 RC는 RC = (1/2) x 384 x (1 - 4/1000 x 2.604) = 48kN입니다. 따라서, 정답은 "48"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 그림과 같이 단순보에 집중하중 P가 보의 중앙점 C에 작용할 때, C점의 수직처짐의 크기는? (단, AB 및 DE 구간의 휨강성은 EI이고, BD 구간은 강체이며, 보의 자중은 무시한다)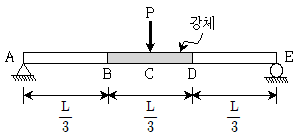

(정답률: 30%)
  • 보의 중앙점 C에 작용하는 하중 P는 보의 중심축에 대해 대칭이므로, 보는 균형상태에 있다. 따라서 보의 수직처짐은 없다. 따라서 정답은 "" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 그림과 같이 휨강성 EI가 일정한 내민보에서 자유단 C점의 처짐이 0이 되기 위한 하중의 크기 비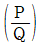는? (단, 자중은 무시한다)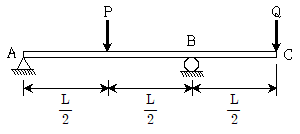

  1. 1
  2. 2
  3. 4
  4. 8
(정답률: 40%)
  • 해당 내민보는 양방향으로 균일하게 분포하고 있으므로, 중간점 D에서의 하중은 전체 하중의 절반인 10kN이다. 이 때, C점에서의 처짐을 구하기 위해서는 C점에서 왼쪽으로 가는 부분과 오른쪽으로 가는 부분을 각각 계산해야 한다.

    왼쪽 부분에서의 처짐은 다음과 같다.

    $$delta_L = frac{FL^3}{3EI}$$

    오른쪽 부분에서의 처짐은 다음과 같다.

    $$delta_R = frac{(10-F)L^3}{3EI}$$

    따라서, 전체 처짐은 다음과 같다.

    $$delta = delta_L + delta_R = frac{FL^3}{3EI} + frac{(10-F)L^3}{3EI} = frac{10L^3}{3EI}$$

    여기서 처짐이 0이 되기 위해서는 F가 4kN이 되어야 한다.

    따라서, 정답은 "4"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >