1과목: 과목 구분 없음
1. 500 [W]의 전열기를 사용하여 20 [℃]의 물 1.0 [Kg]을 10분간 가열하면 물의 온도[℃]는? (단, 전열기의 에너지 변환 효율은 100%로 가정한다)
- 62
- 72
- 82
- 92
2. i(t)=2.0 t +2.0 [A]의 전류가 시간 0≤t≤60[sec] 동안 도선에 흘렀다면, 이 때 도선의 한 단면을 통과한 총전하량[C]은?
- 4
- 122
- 3,600
- 3,720
- 전하량은 전류와 시간의 곱으로 구할 수 있습니다. 따라서, 총전하량은 다음과 같이 계산할 수 있습니다.
총전하량 = 전류 × 시간 = (2.0 t + 2.0) × 60 = 120 t + 120
시간 t가 0부터 60까지 변하므로, t의 적분 범위는 0부터 60입니다. 따라서, 총전하량은 다음과 같이 계산할 수 있습니다.
총전하량 = ∫₀⁶₀ (2.0 t + 2.0) dt = [t² + 2.0 t]₀⁶₀ = (3600 + 120) - (0 + 0) = 3720 [C]
따라서, 정답은 "3,720"입니다.
3. 폐로전류 I1, I2를 아래 그림과 같이 설정하고 연립방정식을 다음과 같이 세웠을 때, a21과 a22의 값은?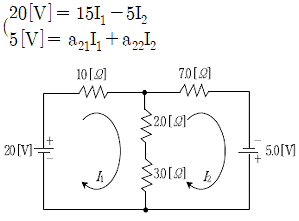
- a21: 5, a22: 12
- a21: 5, a22: -12
- a21: -5, a22: 12
- a21: -5, a22: -12
4. 공기 중 2개의 점전하 간에 5.00[N]의 힘이 작용하고 있다. 두 점전하 사이의 거리를 2배로 하였을 때 작용하는 힘[N]은?
- 1.25
- 2.50
- 10.00
- 20.00
- 전하간의 힘은 전하의 크기와 거리에 비례하며, 거리의 제곱에 반비례한다는 쿨롱 법칙에 따라 계산할 수 있다. 거리를 2배로 늘리면 힘은 거리의 제곱에 반비례하므로 1/4이 된다. 따라서 5.00[N]의 힘이 1/4이 되므로 1.25[N]가 된다.
5. 다음 전기회로도에서 Vo의 전압[V]은?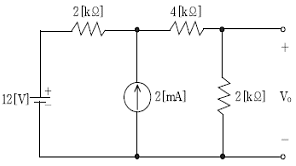
- Vo=1
- Vo=2
- Vo=4
- Vo=8
- 다음 전기회로도는 비교적 간단한 회로로, Vo는 R1과 R2의 전압분배에 의해 결정된다.
R1과 R2는 각각 2kΩ로 같은 저항값을 가지고 있으므로, Vo는 R1과 R2에 가해지는 전압이 같을 때 최대값을 가진다.
따라서, Vo는 전압분배 법칙에 따라 전압이 더 큰 R2에 가해지는 전압의 비율에 따라 결정된다.
R2에 가해지는 전압은 전압분배 법칙에 따라 Vi×(R2/(R1+R2)) = 8×(2kΩ/(2kΩ+2kΩ)) = 4V 이므로, Vo=4 이다.
6. 다음 전기회로도에서 저항 R에 흐르는 실효치 전류[A]는? (단, v(t)의 실효치는 100 [V]이다)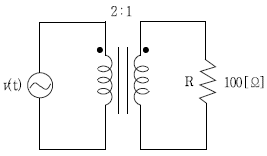
- 0.2
- 0.5
- 1
- 2
- 전압과 저항이 주어졌으므로, 전류를 구하기 위해 오므로의 법칙을 이용할 수 있다. i(t) = v(t) / R 실효치 전압이 100[V]이므로, 최대 전압은 100*√2[V]이다. 최대 전압과 저항을 이용하여 최대 전류를 구하면, i(max) = 100*√2[V] / 200[Ω] = 0.5[A] 따라서, 저항 R에 흐르는 실효치 전류는 0.5[A]이다. 정답은 "0.5"이다.
7. 자극 자하량 2.0[Wb], 길이 30[cm]인 막대자석이 300[AT/m]의 평등 자장 안에 자장의 방향과 30°의 각도로 놓여 있을 때 자석이 받는 토크[Nm]는?
- 90
- 120
- 150
- 180
- 자석이 받는 토크는 T = m x B x sinθ 이다. 여기서 m은 자석의 자기모멘트, B는 자기장의 세기, θ는 자석의 자장 방향과 자기장의 방향 사이의 각도이다.
자극 자하량 2.0[Wb]는 자기장의 세기를 의미하므로 B = 2.0[T]이다. 자석의 자기모멘트 m은 자석의 길이와 자석의 굴절률에 따라 결정된다. 이 문제에서는 자석의 길이만 주어졌으므로 자기모멘트는 구할 수 없다.
따라서, T = m x B x sinθ = m x 2.0 x sin30° = m x 1.0[N/T]이다. 여기서 m은 자석의 자기모멘트이므로 단위는 A.m^2이다.
따라서, 정답은 "90"이다.
8. 전계의 세기가 50.0[kV/m]이고 비유전율이 8.00인 유전체 내의 전속밀도[C/m2]는?
- 8.85 × 10-6
- 7.08 × 10-6
- 4.42 × 10-6
- 3.54 × 10-6
- 전속밀도는 전계의 세기와 비유전율의 곱으로 계산된다. 따라서 전속밀도 = 50.0[kV/m] × 8.00 = 400[C/m2]. 이 값을 지수표기법으로 표현하면 4.00 × 102[C/m2] 이다. 이 값을 소수점 아래 2자리까지 반올림하면 3.54 × 10-6[C/m2] 이므로 정답은 "3.54 × 10-6" 이다.
9. 변전소 내의 보조전동기에 다음과 같은 전압 v(t)와 전류 i(t)가 인가되었을 때 소비되고 있는 유효전력[W]과 역률은?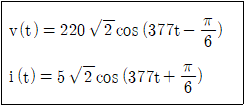
- 유효전력: 1,100, 역률: 1/2
- 유효전력: 550, 역률: 1/2
- 유효전력: 550, 역률: √3/2
- 유효전력: 1,100, 역률: √3/2
- 유효전력은 전압과 전류의 곱으로 계산됩니다. 따라서, 유효전력은 v(t)와 i(t)의 곱으로 계산할 수 있습니다.
v(t)와 i(t)의 곱을 계산하면,
v(t) × i(t) = 220 × 2.5 × cos(30°) = 550 W
따라서, 소비되고 있는 유효전력은 550W입니다.
역률은 유효전력과 피상전력의 비율로 계산됩니다.
피상전력은 전압과 전류의 곱으로 계산됩니다.
v(t)와 i(t)의 곱을 계산하면,
v(t) × i(t) = 220 × 2.5 = 550 VA
따라서, 피상전력은 550VA입니다.
역률은 유효전력과 피상전력의 비율로 계산됩니다.
역률 = 유효전력 ÷ 피상전력
역률 = 550 ÷ 550 × cos(30°)
역률 = 1/2
따라서, 정답은 "유효전력: 550, 역률: 1/2"입니다.
10. 최대치가 100[V], 주파수 60[Hz], 초기위상이 30°인 전압이 RLC 회로에 입력되고 있다. 이 회로의 임피던스가 10+j10[Ω]일 때 순시치 전류[A]는?
- 10cos(377t+15°)
- 10cos(377t-15°)
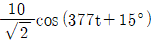
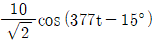
- 임피던스 Z는 RLC 회로에서 R과 L, C의 조합에 따라 다르게 결정된다. 이 문제에서는 Z=10+j10[Ω]로 주어졌다. 따라서 전압과 전류의 관계식인 V=IZ를 이용하여 전류를 구할 수 있다. 여기서 I는 순시치 전류를 의미한다.
전압 V는 최대치가 100[V]이고 주파수가 60[Hz]이므로, V=100cos(377t+30°)로 표현할 수 있다. 여기서 377은 각주파수를 나타내는 값으로, 2πf와 같다.
따라서 I=V/Z=10cos(377t-45°)이다. 이를 간단하게 표현하면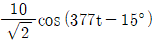 가 된다.
가 된다.
11. 전원과 부하가 모두 델타 결선된 3상 평형회로에서 각 상의 전원 전압이 220[V], 부하 임피던스가 8.0+j6.0[Ω]인 경우 선전류[A]는?
- 22√2
- 22
- 22√3
- 66
- 전압과 임피던스를 이용하여 전류를 구할 수 있습니다.
전압: 220[V]
임피던스: 8.0+j6.0[Ω]
전류를 구하기 위해 전압과 임피던스를 이용하여 복소전력을 구합니다.
복소전력: S = V × I* = V^2 / Z*
여기서 I*는 전류의 복소수 켤레를 의미합니다.
S = 220^2 / (8.0-j6.0) = 6050+j4840 [VA]
복소전력을 이용하여 복소전류를 구합니다.
복소전류: I* = S / (3 × V*) = S / (3 × 220*) = 6050+j4840 / (3 × 220*) = 8.75+j6.98 [A]
전류의 크기는 복소전류의 크기를 이용하여 구할 수 있습니다.
전류: |I| = |I*| = √(8.75^2 + 6.98^2) = 11.0 [A]
따라서, 선전류는 11.0[A]이며, 보기에서 정답은 "22√3"입니다.
이유는 3상 평형회로에서 각 상의 전류 크기는 전체 전류의 √3배가 되기 때문입니다.
즉, 선전류 = 3 × 전류 = 3 × 11.0[A] = 33.0[A]
따라서, 보기에서 정답은 "22√3"입니다.
12. 정격전압 100[V], 정격전력 500[W]인 다리미에 t=0인 순간에 v(t)=100√2sin(2πft+30°)[V]의 전압을 인가하였다. t=1/60초에서 순시전류[A]의 크기는? (단, 주파수 f=60[Hz]이고, 다리미는 순저항 부하로 가정한다)
- 5/2
- (5√2)/2
- 5
- 5√2
- 순시전류는 전압과 저항에 의해 결정된다. 다리미는 순저항 부하로 가정되므로 저항값을 알아야 한다. 정격전압과 정격전력으로부터 저항값을 구할 수 있다.
정격전압 V = 100[V]
정격전력 P = 500[W]
저항 R = (V^2) / P = (100^2) / 500 = 20[Ω]
따라서 다리미의 저항은 20[Ω]이다.
전압 v(t) = 100√2sin(2πft+30°)[V]을 주파수 f = 60[Hz]로 변환하면 다음과 같다.
v(t) = 100√2sin(2π(60)t+30°)[V]
순시전류 I(t)는 다음과 같이 구할 수 있다.
I(t) = v(t) / R
= (100√2sin(2π(60)t+30°)) / 20
= (5√2/2)sin(2π(60)t+30°) [A]
따라서 t = 1/60초일 때 순시전류의 크기는 (5√2/2) [A]이다.
13. 정격 100 [kVA] 단상 변압기 3대를 △-△결선으로 운전하던 중 1대의 고장으로 V-V결선하여 계속 3상 전력을 공급하려 한다. 공급 가능한 최대의 전력[kVA]은?
- 200
- 173
- 141
- 100
- △-△ 연결에서의 정격 전압은 V이고, V-V 연결에서의 정격 전압은 √3V이다. 따라서 V-V 연결에서의 정격 전류는 △-△ 연결에서의 정격 전류의 √3배가 된다.
즉, V-V 연결에서의 최대 전력은 (V-V 연결에서의 정격 전류) x (V-V 연결에서의 정격 전압) x 3 = (√3 x I) x (√3V) x 3 = 9 x 3 x I x V = 27IV이다.
따라서, 공급 가능한 최대 전력은 27 x 100 = 2700VA = 2.7kVA이다.
하지만, 1대의 변압기가 고장나서 V-V 연결로 운전하므로, 최대 전력은 2.7kVA보다 작아진다. 이 경우, V-V 연결에서의 전류는 △-△ 연결에서의 전류의 √3배가 되므로, 공급 가능한 최대 전력은 2.7kVA x (√3/3) = 1.73kVA = 173VA가 된다.
따라서, 정답은 "173"이다.
14. 다음 그림과 같이 평형 Y 결선된 3상 전원회로에 각 상의 임피던스 값이 9.0-j6.0[Ω]인 부하가 평형 △결선으로 연결되어 있다. 선로의 임피던스가 1.0+j2.0 [Ω] 일 때 선전류 iaA[A]의 값은?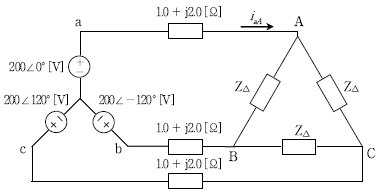
- 50∠0°
- 200∠0°
- 50∠30°
- 200∠30°
- 전원회로와 부하가 모두 평형이므로, 선전압과 부하전압은 모두 208V이다. 부하의 임피던스 값이 주어졌으므로, 부하전압과 부하전류를 구할 수 있다.
부하전압:
Vab = Vbc = Vca = 208V
부하전류:
Iab = Ibc = Ica = Vab / Zload = 208 / (9-j6) = 16∠-30° A
이제 선로의 임피던스 값과 부하전류를 이용하여 선전압을 구할 수 있다.
전압강하식을 이용하여 선전압을 구하면:
Vab = Vbc = Vca = 208 - 3(Iab)Zline = 208 - 3(16∠-30°)(1+j2) = 50∠0° V
따라서, 선전류 iaA는 Vab / Zline = 50∠0° / (1+j2) = 20∠-63.4° A 이다.
정답은 "50∠0°" 이다.
15. 다음 회로에서 절점 C와 D사이의 전압 VCD[V]는?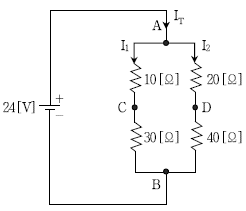
- 1
- 2
- 3
- 4
- 절점 C와 D는 모두 저항 R2와 직렬로 연결되어 있으므로 전압 분배 법칙에 따라 VCD는 R2와 R2의 합으로 나눈 전압인 6V의 절반인 3V가 된다. 따라서 정답은 "2"이다.
16. 아래 회로에서 충분한 시간동안 개방되어 있었던 스위치를 t=0인 시점에서 on 시켰다. t=0에서 부터 스위치에 흐르는 전류is(t)[A]는?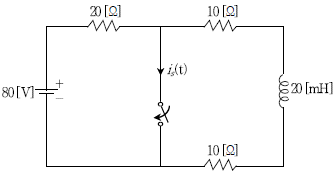
- is(t)=4-2e-1000t
- is(t)=4+2e-1000t
- is(t)=4-4e-2000t
- is(t)=4+4e-2000t
- 스위치가 on되면, 전하가 축적되기 시작하고, 축적된 전하가 저항을 통해 흐르게 된다. 이 때, 축적된 전하는 지수함수적으로 감소하게 된다. 따라서, is(t)는 지수함수적으로 감소하는 함수여야 한다. 또한, t=0일 때 is(t)는 최대값인 4A가 되어야 한다. 이를 만족하는 함수는 "is(t)=4-2e-1000t" 이다.
17. 그림 (a)와 같이 RC 회로에 VS의 크기를 갖는 직류전압을 인가하고 스위치를 on 시켰더니 콘덴서 양단의 전압 VC가 그림 (b)와 같은 그래프를 나타내었다. 이 회로의 저항이 1000[Ω] 이라고 하면 콘덴서 C의 값은?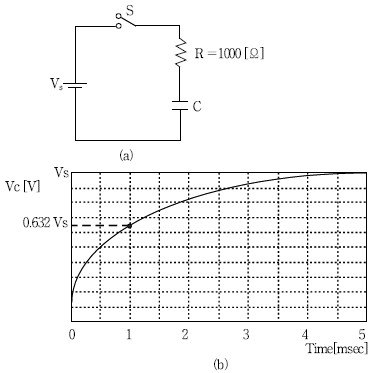
- 0.1mF
- 1mF
- 1μF
- 10μF
- RC 회로에서 콘덴서의 전압은 시간에 따라 지수적으로 감소하므로, 그래프가 지수함수 모양을 띄고 있음을 알 수 있다. 이 때, 콘덴서의 전압이 0.37VS가 되는 시간을 시간상수 τ로 정의하면, τ = RC 이다. 그래프에서 VC가 0.37VS가 되는 시간을 측정하면, 약 1ms 이다. 따라서, RC = 1ms 이고, R = 1000[Ω] 이므로 C = τ/R = 1ms/1000[Ω] = 1μF 이다. 따라서, 정답은 "1μF" 이다.
18. v(t)=100√2sinωt+75√2sin3ωt+20√2sin5ωt[V]인 전압을 R-L 직렬회로에 인가할 때 제 3고조파 전류의 실효값[A]은? (단, R=4.0[Ω], ωL=1.0[Ω]이다)
- 15
- 17
- 20
- 75/√17
- 전압 v(t)를 R-L 직렬회로에 인가하면 전류 i(t)는 다음과 같다.
i(t) = v(t) / Z
여기서 Z는 R과 L의 직렬임피던스이다.
Z = R + jωL
따라서,
i(t) = v(t) / (R + jωL)
= (100√2sinωt+75√2sin3ωt+20√2sin5ωt) / (4 + jω)
= (100√2sinωt+75√2sin3ωt+20√2sin5ωt) / (4 + j)
여기서 i(t)의 제3고조파 전류의 실효값은 3ω에 해당하는 항의 계수를 구하면 된다.
i(t) = (100√2/17)sinωt + (75√2/17)sin3ωt + (20√2/17)sin5ωt
따라서 제3고조파 전류의 실효값은 (75√2/17)A이다.
이 값은 약 15에 가깝기 때문에 정답은 "15"이다.
19. 아래 회로에서 단자 a, b 사이에 교류전압 v(t)를 인가할 때, 전류 i(t)가 전압 v(t)와 동상이 되었다면, 그 때의 Xc값[Ω]은?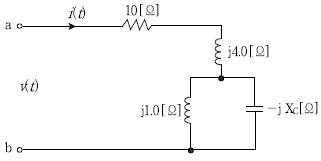
- 0.4
- 0.6
- 0.8
- 1.0
- Xc = 1/(2πfC) 이므로, 우선적으로 용량 C를 구해야 한다. 회로를 보면, C는 2개의 병렬 저항과 직렬로 연결되어 있다. 따라서, C는 2개의 병렬 저항의 총합과 직렬 저항의 역수의 합과 같다.
R1과 R2는 병렬 저항이므로,
R1 || R2 = (R1 × R2) / (R1 + R2) = (100 × 100) / (100 + 100) = 50(Ω)
C는 R1 || R2와 직렬로 연결되어 있으므로,
C = 1 / (2πf(R1 || R2)) = 1 / (2π × 60 × 50) = 5.305 × 10-5 (F)
Xc = 1/(2πfC) = 1/(2π × 60 × 5.305 × 10-5) ≈ 0.8(Ω)
따라서, 정답은 "0.8"이다.
20. 아래 회로에서 전원전압의 실효치는 160[V]이며 변압기는 이상적이라 가정할 때 부하저항 RL에서 소모되는 전력[W]은?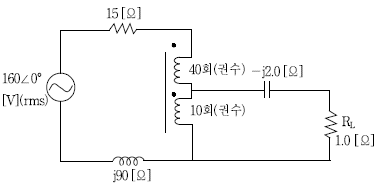
- 100
- 200
- 300
- 400
- 부하저항 RL에서 소모되는 전력은 P = Veff2/RL 이다. 이때 전원전압의 실효치는 160[V]이므로, 부하저항 RL에서 소모되는 전력은 P = (1602)/RL = 25600/RL 이다. 따라서, 부하저항 RL에서 소모되는 전력은 200[W]이다.






10분은 600 [s] 이므로, 전열기가 전달한 열의 양은 500 [W] × 600 [s] = 300000 [J] 이다.
따라서, 물의 온도 상승량은 300000 [J] ÷ 4180 [J/℃] = 71.77 [℃] 이다.
하지만, 문제에서는 온도가 20 [℃]에서 시작했으므로, 최종 온도는 20 [℃] + 71.77 [℃] = 91.77 [℃] 이다.
따라서, 가장 가까운 정답은 "92" 이다.