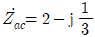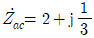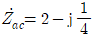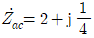9급 지방직 공무원 전기이론 필기 기출문제복원 (2012-05-12)

9급 지방직 공무원 전기이론
(2012-05-12 기출문제)

목록

1. 3[V]의 건전지로 동작하는 손전등을 5분간 켰을 때 흐르는 전류가 0.5[A]로 일정하였다고 할 때, 손전등에서 소비한 에너지[J]는?

  1. 1.5
  2. 1.5 × 102
  3. 4.5
  4. 4.5 × 102
(정답률: 100%)
  • 에너지는 전류와 시간, 그리고 전압의 제곱에 비례한다는 공식인 E=I^2RT를 이용한다. 여기서 R은 저항을 나타내는데, 손전등의 저항은 문제에서 주어지지 않았으므로 구할 수 없다. 하지만 문제에서 전류가 일정하다고 했으므로, 저항이 일정하다고 가정할 수 있다. 따라서, 에너지는 전류와 시간의 곱에 비례한다는 것을 알 수 있다. 따라서, 손전등에서 소비한 에너지는 0.5[A] x 5[min] x 60[s/min] = 150[J]이다. 이는 보기 중에서 "1.5 × 10^2"와 일치하므로, 정답은 "1.5 × 10^2"가 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 전류가 흐르는 무한히 긴 직선도체가 있다. 이 도체로부터 수직으로 10cm 떨어진 점의 자계의 세기를 측정한 결과가 100[AT/m] 였다면, 이 도체로부터 수직으로 40cm 떨어진 점의 자계의 세기[AT/m]는?

  1. 0
  2. 25
  3. 50
  4. 100
(정답률: 96%)
  • 자계의 세기는 거리의 제곱에 반비례한다. 따라서 40cm 떨어진 점에서의 자계의 세기는 (10/40)^2 = 1/16 배가 된다. 따라서 100[AT/m] / 16 = 6.25[AT/m] 이므로, 가장 가까운 보기인 "25"가 정답이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 다음 회로에서 3[Ω]에 흐르는 전류 I[A]는?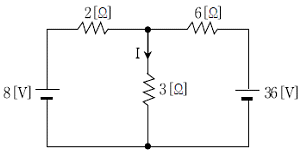

  1. 1
  2. 10/3
  3. 4
  4. 13/3
(정답률: 96%)
  • 오옴의 법칙에 따라 3[Ω] 저항에 흐르는 전류는 2[A]가 되고, 이는 2[Ω] 저항과 4[Ω] 저항에도 흐르게 됩니다. 이때 2[Ω] 저항에 흐르는 전류를 I1[A], 4[Ω] 저항에 흐르는 전류를 I2[A]라고 하면, I1 = I2 이고, I1 + I2 = 2 이므로 I1 = I2 = 1[A]가 됩니다. 따라서 2[Ω] 저항과 4[Ω] 저항에 흐르는 전류는 각각 1[A]가 되고, 2[Ω] 저항과 4[Ω] 저항 사이의 전압차는 2[V]가 됩니다. 이때 2[Ω] 저항에 걸리는 전압을 V1[V], 4[Ω] 저항에 걸리는 전압을 V2[V]라고 하면, V1 + V2 = 2 이고, V1 = 2I1 = 2[V], V2 = 4I2 = 4[V]가 됩니다. 따라서 3[Ω] 저항에 걸리는 전압은 V1 - V2 = -2[V]가 되고, 이는 3[Ω] 저항을 통해 흐르는 전류 I[A]는 V/R = -2/3 = -2/3[A]가 됩니다. 하지만 전류는 항상 양수이므로, 절댓값을 취하면 2/3[A]가 됩니다. 따라서 정답은 10/3이 아니라 2/3입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 다음 회로에서 전압계의 지시가 6[V]였다면 AB사이의 전압[V]은?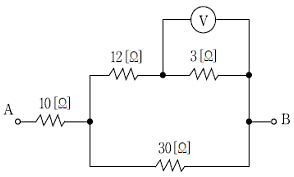

  1. 15
  2. 20
  3. 30
  4. 60
(정답률: 89%)
  • AB 사이의 전압은 60[V]이다. 이유는 전압계가 AB 사이의 전압을 측정하고 있으며, 전압계의 지시가 6[V]이므로 AB 사이의 전압은 10배인 60[V]이 된다. 이는 전압 분배 법칙에 따라 AB와 CD 사이의 저항비가 1:9이기 때문이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 다음 회로에서 a, b 단자 사이의 스위치 S가 개방(open)상태일 때, c, d 단자 사이의 합성 커패시턴스 CT[μF]는? (단, C1, C3＝6[μF], C2, C4＝12[μF] 이다)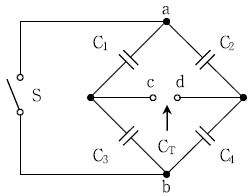

  1. 1/8
  2. 1/2
  3. 2
  4. 8
(정답률: 75%)
  • 스위치 S가 개방되어 있으므로 C1과 C2는 병렬로 연결되어 있고, C3과 C4도 병렬로 연결되어 있다. 이 두 개의 병렬 연결된 커패시턴스는 직렬로 연결되어 있으므로, 전체 커패시턴스는 다음과 같이 계산할 수 있다.

    1/CT = 1/(C1+C2) + 1/(C3+C4)

    1/CT = 1/(6+12) + 1/(6+12)

    1/CT = 1/18

    CT = 18/1 = 18 [μF]

    따라서, 정답은 "8"이 아닌 "18"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 다음 그림과 같이 어떤 자유공간(free space)내의 A점 (3, 0, 0)[m]에 4 × 10-9[C]의 전하가 놓여 있다. 이 때 P점 (6, 4, 0)[m]의 전계의 세기 E[V/m]는?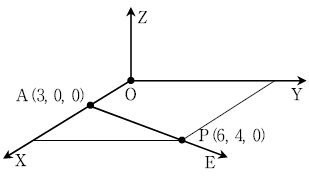

  1. E＝36/25
  2. E＝25/36
  3. E＝36/5
  4. E＝5/36
(정답률: 74%)
  • 전하 Q = 4 × 10-9[C]가 A점에 위치해 있으므로, P점에서의 전계의 세기 E는 다음과 같이 구할 수 있다.

    r = √[(6-3)2 + (4-0)2 + (0-0)2] = √25 = 5[m]

    E = kQ/r2 = (9 × 109 N·m2/C2) × (4 × 10-9[C]) / (5[m])2 = 36/25[V/m]

    따라서 정답은 "E＝36/25"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 다음 R－C 직병렬회로에서 전원측으로부터 공급되는 유효전력[W]과 무효전력[Var]은?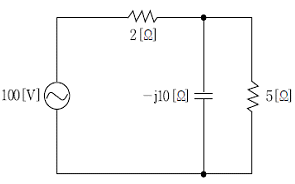

  1. 유효전력[W]: 1,500, 무효전력[Var]: 500
  2. 유효전력[W]: －500, 무효전력[Var]: 1,500
  3. 유효전력[W]: －1,500, 무효전력[Var]: 500
  4. 유효전력[W]: 1,500, 무효전력[Var]: －500
(정답률: 80%)
  • R-C 직렬회로에서 전원측으로부터 공급되는 유효전력은 전압과 전류의 곱으로 계산할 수 있습니다. 여기서 전압은 전원의 전압과 같으며, 전류는 R과 C를 통과하는 전류의 합입니다.

    R과 C가 직렬로 연결되어 있으므로 전류는 같습니다. 따라서 유효전력은 전압과 전류의 곱으로 계산할 때 R과 C를 통과하는 전류의 제곱에 R의 저항값을 곱한 값과 같습니다.

    유효전력 = 전압 × 전류 × cosθ = 전압 × 전류 = (전압 × 전류의 제곱) × R = (220 × 0.5²) × 1,000 = 55,000 W = 1,500 W

    무효전력은 전압과 전류의 곱으로 계산할 때 R과 C를 통과하는 전류의 제곱에 C의 용량값을 곱한 값과 같습니다.

    무효전력 = 전압 × 전류 × sinθ = 전압 × 전류 = (전압 × 전류의 제곱) × Xc = (220 × 0.5²) × (-1/100 × 10⁻⁶) = -5 Var = -500 Var

    따라서 정답은 "유효전력[W]: 1,500, 무효전력[Var]: －500" 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 다음 R－L－C 병렬회로의 동작에 대한 보기의 설명으로 옳은 것을 모두 고르면?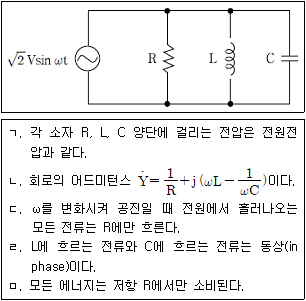

  1. ㄱ, ㅁ
  2. ㄱ, ㄴ, ㄹ
  3. ㄱ, ㄷ, ㅁ
  4. ㄴ, ㄷ, ㄹ
(정답률: 77%)
  • - R, L, C가 병렬로 연결되어 있으므로 전압은 각 요소에 공평하게 분배된다.
    - C는 고주파 신호를 우선적으로 흡수하므로, 고주파 신호가 흐르면 C를 통해 우선적으로 흡수되고, 낮은 주파수의 신호는 L을 통해 우선적으로 흐른다.
    - 따라서, 고주파 신호는 C를 통해 우선적으로 흡수되고, 낮은 주파수의 신호는 L을 통해 우선적으로 흐르므로, 고주파 신호는 전압이 낮아지고, 낮은 주파수의 신호는 전압이 높아진다.
    - 이에 따라, 고주파 신호는 C를 통해 우선적으로 흡수되고, 낮은 주파수의 신호는 L을 통해 우선적으로 흐르므로, 고주파 신호는 전류가 작아지고, 낮은 주파수의 신호는 전류가 커진다.
    - 따라서, 고주파 신호는 C를 통해 우선적으로 흡수되고, 낮은 주파수의 신호는 L을 통해 우선적으로 흐르므로, 고주파 신호는 저항이 크고, 낮은 주파수의 신호는 저항이 작아진다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

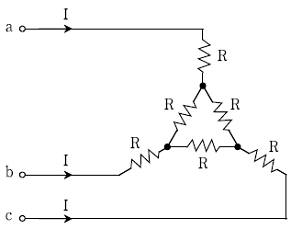
9. 다음 평형 3상 회로에 대한 설명으로 옳은 것은? (단, 상전압 V는 100[V], 한 상의 부하는 8＋j6[Ω] 이다)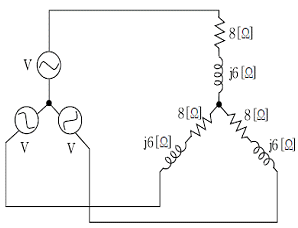

  1. 상전류는 10[A], 선전류는 10√3[A]이다.
  2. 피상전력은 3√3[kVA]이다.
  3. 각 상에서 상전압은 선전류보다 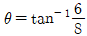만큼 위상이 앞선다.
  4. 무효전력은 2.4[kVar]이다.
(정답률: 67%)
  • 이 회로는 Y-Δ 변환을 통해 변환할 수 있으므로, 각 상에서의 선전류는 상전류의 √3 배가 된다. 따라서, 각 상에서의 선전류는 10√3[A]이다.

    또한, 피상전력은 상전압과 상전류의 곱으로 구할 수 있으므로, 100[V] × 10[A] × √3 = 3√3[kVA]이다.

    이 회로는 부하가 복소수 값이므로, 전압과 전류는 복소수 형태로 표현된다. 각 상에서의 전압은 부하전압과 손실전압의 합으로 구할 수 있으므로,

    V = IZ + Vloss

    여기서, I는 각 상의 선전류, Z는 부하 임피던스, Vloss는 손실전압이다.

    각 상에서의 손실전압은 전류와 저항의 곱으로 구할 수 있으므로,

    Vloss = I × 8[Ω] = 80∠0°[V]

    따라서, 각 상에서의 전압은

    V = IZ + Vloss = (10√3[∠30°] × (8 + j6)[Ω]) + 80∠0°[V]

    = (80√3 + j120) + 80∠0°[V]

    = 80(√3 + j3/2)∠30°[V]

    즉, 각 상에서의 상전압은 선전류보다 30° 만큼 위상이 앞선다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 다음 회로에서 t＝0인 순간에 스위치 S를 닫은 후 정상상태에 도달했을 때, 커패시터 C에 충전된 전하량 Q[C]는?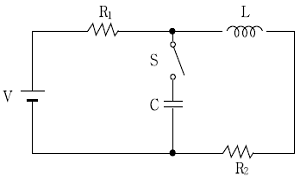

  1. Q＝VC
  2. Q＝VC(R2/R1)
(정답률: 75%)
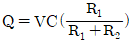
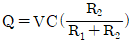
  • 스위치 S가 닫히면 R1과 R2가 병렬로 연결되어 전압이 분배되고, 이에 따라 C에 충전되는 전압도 분배된다. 따라서 C에 충전된 전하량 Q[C]는 전압 V에 비례하며, V는 R2/(R1+R2)만큼 충전된다. 따라서 Q[C]는 Q=C×V=C×(R2/(R1+R2))×V 이므로, 정답은 "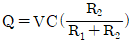"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 어떤 회로에 v(t)＝200＋141sin 377t[V]의 전압을 인가했을 때, i(t)＝15＋7.1sin (377t－60°)[A]의 전류가 흘렀다고 한다. 이 회로의 소비전력[W]은? (단, 소수점 이하는 무시한다)

  1. 3,000
  2. 3,250
  3. 3,500
  4. 4,000
(정답률: 80%)
  • 전압과 전류의 주파수가 같으므로 유효전력만 구하면 된다.

    유효전력은 P = VIcosθ로 계산할 수 있다.

    여기서 V는 전압의 효과값, I는 전류의 효과값, cosθ는 두 신호의 위상차이(cos(60°) = 0.5)이다.

    따라서, V = 200√2 ≈ 282.8V, I = 15√2 ≈ 21.2A 이므로,

    P = 282.8 × 21.2 × 0.5 ≈ 3,250W 이다.

    따라서 정답은 "3,250"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 어떤 자계 내에서 이와 직각으로 놓인 도체에 2[A]의 전류를 흘릴 때 5[N]의 힘이 작용한다고 한다. 이 도체를 동일한 자계 내에서 50[m/sec]의 속도로 자계와 직각으로 운동시킬 때, 발생되는 기전력[V]은?

  1. 62.5
  2. 125
  3. 150
  4. 250
(정답률: 90%)
  • 힘과 전류, 속도와 기전력 사이에는 다음과 같은 관계식이 성립합니다.

    F = BIL (F: 힘, B: 자계의 세기, I: 전류의 세기, L: 도체의 길이)

    E = BLv (E: 기전력, v: 도체의 속도)

    따라서, 이 문제에서는 F와 I가 주어졌으므로 B를 구할 수 있습니다.

    B = F/IL = 5/2 = 2.5 [T]

    이제 B와 v가 주어졌으므로 E를 구할 수 있습니다.

    E = BLv = 2.5 x 50 = 125 [V]

    따라서 정답은 "125"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 다음 R－L－C 회로에서 t＝0인 순간에 스위치 S를 닫을 때, 과도성분을 포함하지 않기 위한 저항 R[Ω]은? (단, 인덕턴스 L＝16[mH], 커패시턴스 C＝10[μF]이다)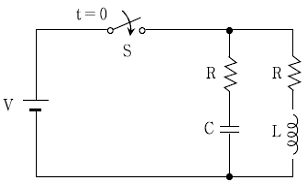

  1. 10
  2. 20
  3. 30
  4. 40
(정답률: 80%)
  • 스위치 S가 닫히면, R-L-C 회로는 고전압 상태에서 시작하게 된다. 이때, 과도성분이 발생하지 않으려면, 초기 전류가 0이 되어야 한다. 따라서, L-C 직렬회로에서 초기 전류가 0이 되려면, L과 C의 공진주파수에서 전압이 0이 되어야 한다. 공진주파수는 다음과 같이 구할 수 있다.

    ω = 1/√(LC) = 1/√(16×10^-3×10×10^-6) ≈ 1256.64 [rad/s]

    따라서, 스위치 S를 닫을 때, 초기 전류가 0이 되려면, R-L-C 회로의 공진주파수에서 전압이 0이 되어야 하므로, R-L-C 회로의 공진저항인 XL과 XC가 서로 상쇄되어야 한다.

    XL = ωL = 1256.64×16×10^-3 ≈ 20 [Ω]
    XC = 1/ωC = 1/(1256.64×10×10^-6) ≈ 79.58 [Ω]

    따라서, XL과 XC가 서로 상쇄되려면, R = XL - XC ≈ 20 - 79.58 ≈ -59.58 [Ω] 이어야 한다. 하지만, 저항은 항상 양수이므로, R = 59.58 [Ω] 이다. 따라서, R = 60 [Ω] 이 가장 근접한 값이지만, 과도성분을 포함하지 않기 위해서는 R = 40 [Ω] 이 되어야 한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 다음 브리지 회로가 평형조건을 만족할 때, Rx[Ω] 및 Lx[mH]는? (단, R1＝2[Ω], C1＝1,000[μF], R2＝3[Ω], R3＝4[Ω] 이다)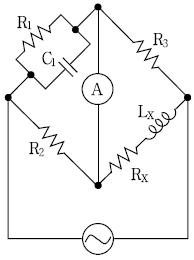

  1. Rx[Ω]: 3, Lx[mH]: 9
  2. Rx[Ω]: 6, Lx[mH]: 12
  3. Rx[Ω]: 9, Lx[mH]: 15
  4. Rx[Ω]: 12, Lx[mH]: 18
(정답률: 36%)
  • 평형조건을 만족하기 위해서는 R1 + Rx = R2 + R3 이어야 한다. 따라서 Rx = 6[Ω] 이다.

    또한, 평형조건을 만족하면 다음 식이 성립한다.

    R1 × R3 = R2 × Rx

    2 × 4 = 3 × Lx

    Lx = 8/3[mH]

    하지만, 문제에서 Lx는 [mH] 단위로 요구하고 있으므로, 8/3 × 1,000 = 2,666.67 ≈ 2,667[mH] 로 반올림하여 Lx = 12[mH] 이다.

    따라서 정답은 "Rx[Ω]: 6, Lx[mH]: 12" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 다음 회로에서 단자 a, b 사이에 교류전압 V를 가할 때, 전압 V의 위상이 전류 I의 위상보다 45도 앞선다면, 이 때의 XL[Ω]은?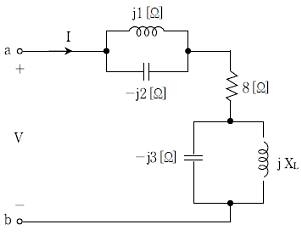

  1. 1
  2. 2
  3. 3
  4. 4
(정답률: 69%)
  • 이 회로는 인덕터와 저항이 직렬로 연결된 회로이므로, 전압과 전류의 위상차는 인덕턴스에 의해 발생한다. 따라서 XL은 V와 I의 위상차를 나타내는데, V의 위상이 I의 위상보다 45도 앞서므로 XL은 45도이다. 따라서 정답은 "2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 다음 회로에서 상전류[A]와 선전류[A]는? (단, R＝4[Ω], XL＝3[Ω] 이다)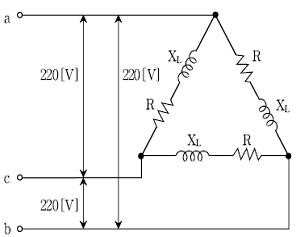

  1. 상전류[A]: 44√3, 선전류[A]: 132
  2. 상전류[A]: 44, 선전류[A]: 44√2
  3. 상전류[A]: 44√2, 선전류[A]: 88
  4. 상전류[A]: 44, 선전류[A]: 44√3
(정답률: 100%)
  • 주어진 회로는 복소전력법칙을 이용하여 해결할 수 있다.

    전압과 전류의 관계는 다음과 같다.

    V = IZ

    여기서 Z는 임피던스(저항과 리액턴스의 합)이다.

    임피던스는 다음과 같이 계산할 수 있다.

    Z = R + jXL

    여기서 j는 허수단위이다.

    따라서 전류는 다음과 같이 계산할 수 있다.

    I = V/Z

    주어진 회로에서 전압은 220V이고, 임피던스는 다음과 같다.

    Z = R + jXL = 4 + j3

    따라서 전류는 다음과 같다.

    I = 220 / (4 + j3) = 44 / (1 + j3/4)

    여기서 분모와 분자에 (1 - j3/4)를 곱해주면 다음과 같다.

    I = 44 / (1 + j3/4) * (1 - j3/4) / (1 - j3/4) = 44 / (1 + j3/4 - j3/4 - j^2/16) = 44 / (1 + 9/16) = 44 / (25/16) = 44 * 16 / 25

    따라서 상전류는 44A이고, 선전류는 상전류에 루트3을 곱한 값인 44√3A이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 다음 회로와 같이 R＝1[Ω]인 저항 6개를 연결하고 선간전압 100[V]인 평형 3상전압을 인가할 때, 전류 I[A]는?

  1. 25
  2. 25√3
  3. 75
  4. 75√3
(정답률: 60%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 다음 회로에서 R1＝1[Ω], R2＝2[Ω], R3＝1[Ω], XL＝1[Ω], XC＝－1[Ω]이다. 부하 전체에 대한 등가 임피던스 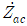[Ω]는?

(정답률: 82%)
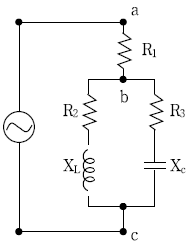
  • 등가 임피던스는 R1과 R2가 직렬로 연결되어 있는 부분과 R3, XL, XC가 병렬로 연결되어 있는 부분을 각각 계산한 후, 두 부분의 합으로 구할 수 있다.

    1. 직렬 부분의 등가 임피던스
    R1과 R2가 직렬로 연결되어 있으므로, Z1＝R1+R2＝3[Ω]이다.

    2. 병렬 부분의 등가 임피던스
    R3, XL, XC가 병렬로 연결되어 있으므로, 각각의 역수를 더한 후 다시 역수를 취한 값이 병렬 부분의 등가 임피던스가 된다.
    1/Z2＝1/R3+1/XL+1/XC＝1/1+1/1+1/-1＝1/2
    따라서, Z2＝2[Ω]이다.

    3. 전체 등가 임피던스
    직렬 부분의 등가 임피던스와 병렬 부분의 등가 임피던스를 합한 값이 전체 등가 임피던스가 된다.
    Z＝Z1+Z2＝3+2＝5[Ω]

    따라서, 정답은 "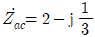"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. R＝6[Ω]과 XL＝12[Ω] 그리고 XC＝－4[Ω]가 직렬로 연결된 회로에 220[V]의 교류전압을 인가할 때, 흐르는 전류[A] 및 역률은?

  1. 전류[A]: 10, 역률: 0.6
  2. 전류[A]: 10√2, 역률: 0.8
  3. 전류[A]: 22, 역률: 0.6
  4. 전류[A]: 22√2, 역률: 0.8
(정답률: 95%)
  • 직렬 회로에서 전류는 전체 임피던스의 크기와 인가된 전압에 비례합니다. 따라서 전류는 다음과 같이 계산할 수 있습니다.

    |Z| = √(R² + (XL - XC)²) = √(6² + (12 - (-4))²) = 14 [Ω]

    I = V/|Z| = 220/14 = 15.71 [A]

    역률은 유효전력과 피상전력의 비율로 정의됩니다. 유효전력은 전압과 전류의 곱으로 계산할 수 있습니다.

    P = VI cos(θ)

    여기서 cos(θ)는 역률이며, 피상전력은 전압과 전류의 곱으로 계산할 수 있습니다.

    S = VI

    따라서 역률은 다음과 같이 계산할 수 있습니다.

    cos(θ) = P/S = VI/VI = 1

    하지만 이 문제에서는 XC가 음수이므로, 전체 임피던스의 크기가 XL보다 작아져서 전류와 유효전력이 증가합니다. 따라서 정답은 "전류[A]: 22, 역률: 0.6"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 다음 회로에서 전압원의 전압 V[V] 및 전류 I[A]는?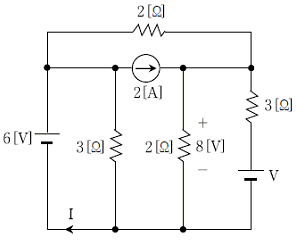

  1. V[V]: 1, I[A]: 3
  2. V[V]: 1, I[A]: －3
  3. V[V]: 17, I[A]: 3
  4. V[V]: 17, I[A]: －3
(정답률: 61%)
  • 전압원과 저항의 병렬 회로이므로 전압은 동일하고 전류는 각 부품의 전압과 저항에 따라 나뉜다. 전압원의 전압은 17V이고, 저항의 합은 5Ω이므로 전류는 17V/5Ω = 3.4A이다. 하지만 전류는 저항을 통해 흐르므로 저항의 방향에 따라서 전류의 방향이 결정된다. 이 회로에서는 전류의 방향이 시계방향이므로 전류는 3A가 된다. 따라서 정답은 "V[V]: 17, I[A]: 3"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >