1과목: 과목 구분 없음
1. 전압원의 기전력은 20[V]이고 내부저항은 2[Ω]이다. 이 전압원에 부하가 연결될 때 얻을 수 있는 최대 부하전력[W]은?
- 200
- 100
- 75
- 50
2. 다음 회로에서 조정된 가변저항값이 100[Ω]일 때 A와 B 사이의 저항 100[Ω] 양단 전압을 측정하니 0[V]일 경우, Rx[Ω]은?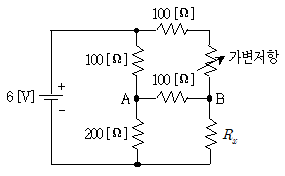
- 400
- 300
- 200
- 100
3. 다음 회로와 같이 직렬로 접속된 두 개의 코일이 있을 때, L1=20[mH], L2=80[mH], 결합계수 k=0.8이다. 이 때 상호 인덕턴스 M의 극성과 크기[mH]는? (순서대로 극성, 크기)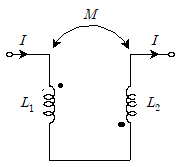
- 가극성, 32
- 가극성, 40
- 감극성, 32
- 감극성, 40
4. 단상 교류전압 v=300√2 cosωt[V]를 전파 정류하였을 때, 정류회로 출력 평균전압[V]은? (단, 이상적인 정류 소자를 사용하여 정류회로 내부의 전압강하는 없다)
- 150
- 300/2π
- 300/π
- (600√2)/π
5. 다음 회로에서 V=96[V], R=8[Ω], XL=6[Ω]일 때, 전체 전류 I[A]는?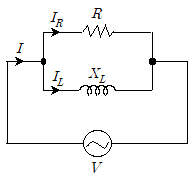
- 38
- 28
- 9.6
- 20
6. 다음 (a)는 반지름 2r을 갖는 두 원형 극판 사이에 한 가지 종류의 유전체가 채워져 있는 콘덴서이다. (b)는 (a)와 동일한 크기의 원형 극판 사이에 중심으로부터 반지름 r인 영역 부분을 (a)의 경우보다 유전율이 2배인 유전체로 채우고 나머지 부분에는 (a)와 동일한 유전체로 채워놓은 콘덴서이다. (b)의 정전용량은 (a)와 비교하여 어떠한가? (단, (a)와 (b)의 극판 간격 d는 동일하다)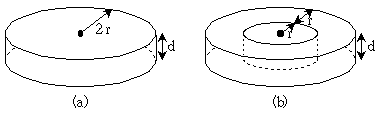
- 15.7% 증가한다.
- 25% 증가한다.
- 31.4% 증가한다.
- 50% 증가한다.
7. 부하임피던스 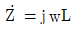 [Ω]에 전압 V[V]가 인가되고 전류 2I[A]가 흐를 때의 무효전력[Var]을 w, L, I로 표현한 것은?
[Ω]에 전압 V[V]가 인가되고 전류 2I[A]가 흐를 때의 무효전력[Var]을 w, L, I로 표현한 것은?
- 2wLI2
- 4wLI2
- 4wLI
- 2wLI
8. 다음 식으로 표현되는 비정현파 전압의 실효값[V]은?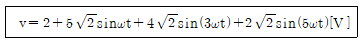
- 13√2
- 11
- 7
- 2
9. 다음 회로 (a), (b)에서 스위치 S1, S2를 동시에 닫았다. 이 후 50초 경과 시 (I1-I2)[A]로 가장 적절한 것은? (단, L과 C의 초기전류와 초기전압은 0이다)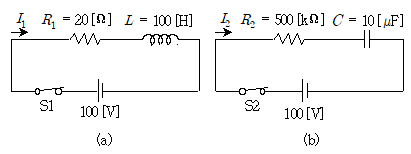
- 0.02
- 3
- 5
- 10
10. 다음 회로와 같이 평형 3상 전원을 평형 3상 Δ결선 부하에 접속하였을 때 Δ결선 부하 1상의 유효전력이 P[W]였다. 각 상의 임피던스 Z를 그대로 두고 Y결선으로 바꾸었을 때 Y결선 부하의 총전력[W]은?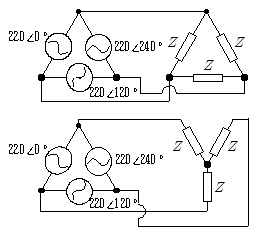
- P/3
- P
- √3 P
- 3P
11. 다음 회로에서 직류전압 Vs = 10[V]일 때, 정상상태에서의 전압 Vc[V]와 전류 IR[mA]은? (순서대로 Vc, IR)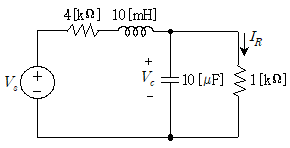
- 8, 20
- 2, 20
- 8, 2
- 2, 2
12. 진공 중의 한점에 음전하 5[nC]가 존재하고 있다. 이 점에서 5[m] 떨어진 곳의 전기장의 세기[V/m]는? (단, 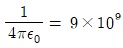 이고, ε0는 진공의 유전율이다)
이고, ε0는 진공의 유전율이다)
- 1.8
- -1.8
- 3.8
- -3.8
13. 철심 코어에 권선수 10인 코일이 있다. 이 코일에 전류 10[A]를 흘릴 때, 철심을 통과하는 자속이 0.001[Wb]이라면 이 코일의 인덕턴스[mH]는?
- 100
- 10
- 1
- 0.1
14. 다음 그림과 같이 자극(N, S) 사이에 있는 도체에 전류 I[A]가 흐를 때, 도체가 받는 힘은 어느 방향인가?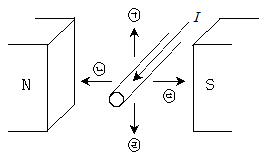
- ㉠
- ㉡
- ㉢
- ㉣
15. 이상적인 단상 변압기의 2차측에 부하를 연결하여 2.2[kW]를 공급할 때의 2차측 전압이 220[V], 1차측 전류가 50[A]라면 이 변압기의 권선비 N1:N2는? (단, N1은 1차측 권선수이고 N2는 2차측 권선수이다)
- 1:5
- 5:1
- 1:10
- 10:1
16. 교류회로의 전압 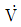 와 전류
와 전류 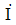 가 다음 벡터도와 같이 주어졌을 때, 임피던스
가 다음 벡터도와 같이 주어졌을 때, 임피던스 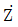 [Ω]는?
[Ω]는?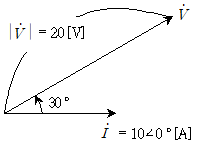
- √3-j
- √3+j
- 1+j√3
- 1-j√3
17. 다음과 같은 정현파 전압 v와 전류 i로 주어진 회로에 대한 설명으로 옳은 것은?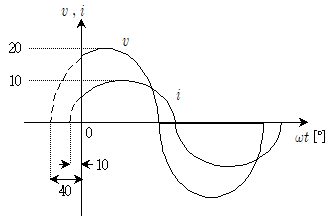
- 전압과 전류의 위상차는 40°이다.
- 교류전압 v=20sin (ωt-40°)이다.
- 교류전류 i=10√2 sin(ωt+10°)이다.
- 임피던스
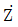 =2∠30°이다.
=2∠30°이다.
18. 다음 회로에서 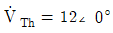 [V]이고
[V]이고 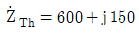 [Ω]일 때, 최대전력을 전달하기 위한 부하임피던스
[Ω]일 때, 최대전력을 전달하기 위한 부하임피던스 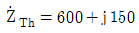 [Ω]과 부하임피던스에 소비되는 전력 PL[W]은? (순서대로
[Ω]과 부하임피던스에 소비되는 전력 PL[W]은? (순서대로 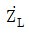 , PL)
, PL)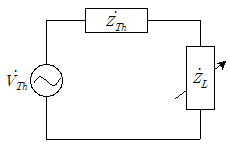
- 600-j150, 0.06
- 600+j150, 0.6
- 600-j150, 0.6
- 600+j150, 0.06
19. 다음 평형 3상 교류회로에서 선간전압의 크기 VL=300[V], 부하 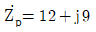 [Ω]일 때, 선전류의 크기 IL[A]는?
[Ω]일 때, 선전류의 크기 IL[A]는?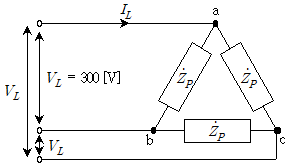
- 10
- 10√3
- 20
- 20√3
20. 다음 회로가 정상상태를 유지하는 중, t=0에서 스위치 S를 닫았다. 이 때 전류 i의 초기전류 i(0+)[mA]는?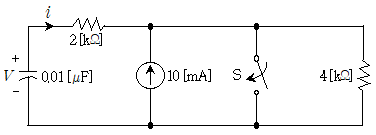
- 0
- 2
- 10
- 20






전류 = 20[V] / (2[Ω] + 부하의 저항)
최대 전력 = 전류^2 x 부하의 저항
부하의 저항이 클수록 최대 전력은 작아지므로, 부하의 저항이 무한대일 때 최대 전력을 구하면 된다.
전류 = 20[V] / (2[Ω] + ∞) = 0[A]
최대 전력 = 0^2 x ∞ = 0
따라서, 최대 부하전력은 0[W]이며, 보기에서 정답은 "50"이 아니다.