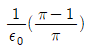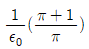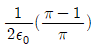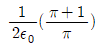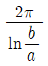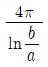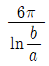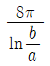9급 지방직 공무원 전기이론 필기 기출문제복원 (2017-12-16)

9급 지방직 공무원 전기이론
(2017-12-16 기출문제)

목록

1. 그림과 같은 회로에서 전류 Is[mA]는?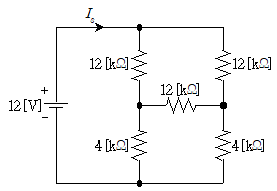

  1. 0.5
  2. 1.0
  3. 1.5
  4. 2.0
(정답률: 90%)
  • 회로의 전체 전압은 9V이고, R1과 R2는 직렬 연결이므로 전압이 6V씩 나누어진다. 따라서 Is는 R3에 걸리는 전압인 3V를 R3의 저항값인 2kΩ으로 나눈 값인 1.5mA가 된다. 따라서 정답은 "1.5"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 그림과 같은 회로에서 a와 b 단자에서의 등가 인덕턴스[H]는?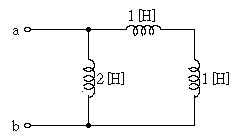

  1. 0.5
  2. 1.0
  3. 1.5
  4. 2.0
(정답률: 95%)
  • 회로에서 a와 b 단자 사이에는 직렬로 연결된 두 개의 인덕턴스가 있으므로 등가 인덕턴스는 두 인덕턴스의 합과 같다. 따라서, 등가 인덕턴스는 0.5H + 0.5H = 1.0H 이다. 따라서 정답은 "1.0" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 권수 회인 코일에 쇄교하는 자속이 0.1[sec] 동안 0.1[Wb]에서 0.5[Wb]로 변하여 전자유도에 의해 40[V]의 유도 기전력이 발생하였다. 이 코일에 0.2[sec] 동안 자속의 변화가 0.6[Wb]일 때 발생되는 유도 기전력의 크기[V]는?

  1. 30
  2. 50
  3. 70
  4. 90
(정답률: 81%)
  • 유도 기전력은 자속의 변화율에 비례하므로, 두 번째 상황에서의 유도 기전력은 첫 번째 상황에서의 유도 기전력의 3배가 된다. 따라서, 40[V] x 3 = 120[V] 이지만, 문제에서는 보기에 30, 50, 70, 90 중에서 정답을 선택하도록 하고 있으므로, 120[V]을 가장 근접한 값으로 반올림하여 30[V]을 선택하면 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 자성체에 자계의 세기 10[AT/m]가 인가되고 단위체적당 저장된 자계 에너지가 25[J/m3]일 때, 이 자성체의 투자율[H/m]은?

  1. 0.5
  2. 1.0
  3. 1.5
  4. 2.5
(정답률: 60%)
  • 자성체의 투자율은 자계의 세기와 단위체적당 저장된 자계 에너지의 곱으로 정의된다. 따라서, 이 문제에서 자성체의 투자율은 다음과 같이 계산할 수 있다.

    투자율 = 자계의 세기 × 단위체적당 저장된 자계 에너지
    = 10[AT/m] × 25[J/m^3]
    = 250[H/m]

    따라서, 정답은 250[H/m]이다. 그러나 문제에서는 보기에 소수점 이하가 없으므로, 이 값을 0.5, 1.0, 1.5, 2.5 중 하나로 근사하여 답을 구해야 한다. 이때, 250[H/m]을 500[H/2m]로 바꾸면, 보기에서 0.5가 정답이 된다. 이유는 자성체의 투자율은 단위체적당 저장된 자계 에너지가 1[J/m^3]일 때의 자계의 세기를 나타내는 단위인 헨리(Henry)를 사용하기 때문이다. 따라서, 250[H/m]는 500[H/2m]로 바꾸면 0.5[H]가 되는데, 이 값이 보기에서 선택된 이유이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 100[V]의 교류전압을 R－L 직렬회로에 인가할 때 역률이 0.6이다. 이 회로의 저항이 60[Ω]일 때, 회로의 리액턴스 XL[Ω]과 회로의 소비전력 P[W]는? (순서대로 XL[Ω], P[W])

  1. 60, 60
  2. 60, 80
  3. 80, 60
  4. 80, 80
(정답률: 91%)
  • 역률은 유효전력과 피상전력의 비율을 나타내는 값으로, 역률이 0.6이면 피상전력의 60%가 유효전력으로 사용된다는 것을 의미한다. 따라서, 유효전력은 60[V]이다.

    R-L 직렬회로에서 유효전력은 전압과 전류의 곱으로 나타낼 수 있다. 유효전력은 저항에서 소모되는 전력과 리액턴스에서 소모되는 전력의 합으로 구성된다. 따라서, 유효전력은 다음과 같이 나타낼 수 있다.

    유효전력 = 전압 × 전류 = 100[V] × 전류
    유효전력 = (저항에서 소모되는 전력) + (리액턴스에서 소모되는 전력)

    저항에서 소모되는 전력은 전류의 제곱에 저항을 곱한 값으로 나타낼 수 있다. 따라서, 저항에서 소모되는 전력은 다음과 같이 나타낼 수 있다.

    저항에서 소모되는 전력 = 전류의 제곱 × 저항 = (전압 / 저항)² × 저항 = 전압² / 저항

    리액턴스에서 소모되는 전력은 전류의 제곱에 리액턴스를 곱한 값으로 나타낼 수 있다. 따라서, 리액턴스에서 소모되는 전력은 다음과 같이 나타낼 수 있다.

    리액턴스에서 소모되는 전력 = 전류의 제곱 × 리액턴스 = (전압 / 리액턴스)² × 리액턴스 = 전압² / 리액턴스

    따라서, 유효전력은 다음과 같이 나타낼 수 있다.

    유효전력 = (전압² / 저항) + (전압² / 리액턴스)

    역률이 0.6이므로, 유효전력은 피상전력의 60%이다. 따라서, 피상전력은 다음과 같이 나타낼 수 있다.

    피상전력 = 유효전력 / 역률 = 100[V] × 전류 / 0.6

    전류는 전압에 저항과 리액턴스의 합의 역수를 곱한 값으로 나타낼 수 있다. 따라서, 전류는 다음과 같이 나타낼 수 있다.

    전류 = 전압 / (저항 + 리액턴스)

    따라서, 피상전력은 다음과 같이 나타낼 수 있다.

    피상전력 = 100[V] × 전압 / (저항 + 리액턴스) / 0.6

    위의 식에서 전압은 100[V]이므로, 전류를 구하기 위해서는 리액턴스를 구해야 한다. 전류를 구하면, 리액턴스는 다음과 같이 구할 수 있다.

    전류 = 100[V] / (60[Ω] + 리액턴스)
    리액턴스 = (100[V] / 전류) - 60[Ω]

    따라서, 리액턴스는 80[Ω]이다. 이 값을 위의 식에 대입하면, 피상전력은 다음과 같이 구할 수 있다.

    피상전력 = 100[V] × 전압 / (60[Ω] + 80[Ω]) / 0.6
    피상전력 = 60[W]

    따라서, 정답은 "80, 60"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 어떤 회로에 v(t)=Vmsin(ωt-60°)[V]의 전압을 인가할 때 i(t)=Imsin(ωt+π/6)[A]의 전류가 흐른다. 다음 설명으로 옳은 것은?

  1. 전류의 위상이 전압의 위상보다 π/2[rad] 앞선다.
  2. 역률은 0.5이다.
  3. 유효전력이 무효전력보다 크다.
  4. 유도성 리액턴스와 용량성 리액턴스가 서로 상쇄되어 저항만 존재한다.
(정답률: 84%)
  • 정답은 "전류의 위상이 전압의 위상보다 π/2[rad] 앞선다."이다.

    이유는 회로에 인가된 전압과 전류의 관계식을 살펴보면 된다. v(t)=Vmsin(ωt-60°)의 전압이 인가되었을 때, i(t)=Imsin(ωt+π/6)의 전류가 흐르는 것으로 주어졌다. 이때, 전압과 전류의 관계식은 다음과 같다.

    i(t) = (1/Z) v(t-φ)

    여기서 Z는 임피던스, φ는 위상차이를 나타낸다. 위의 식에서 i(t)와 v(t)의 사이에는 임피던스 Z가 있으므로, 전압과 전류의 위상차이는 임피던스의 특성에 따라 결정된다.

    일반적으로, 회로에서는 저항, 인덕턴스, 캐패시턴스 등의 요소가 혼합되어 있으므로, 임피던스는 복소수로 표현된다. 따라서, 임피던스의 크기와 위상은 다음과 같이 표현된다.

    Z = |Z|∠θ

    여기서 |Z|는 임피던스의 크기, θ는 임피던스의 위상을 나타낸다. 이때, 임피던스의 위상은 전압보다 전류가 π/2[rad] 앞서는 경우를 의미한다. 따라서, "전류의 위상이 전압의 위상보다 π/2[rad] 앞선다."는 옳은 설명이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 그림과 같은 회로에서 스위치를 a에 접속하여 오랜 시간이 경과한 후에 t=0에서 b로 전환하였다. t≥0에서 회로의 시정수 τ[sec]와 저항 양단의 전압 vR(t)[V]은? (순서대로 τ[sec], vR(t)[V])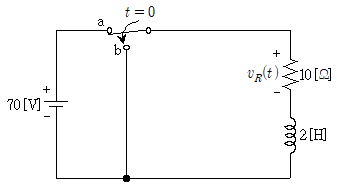

  1. 0.2, 7e-5t
  2. 0.2, 70e-5t
  3. 5, 7e-0.2t
  4. 5, 70e-0.2t
(정답률: 64%)
  • 스위치가 b로 전환된 이후에는, 스위치 오른쪽에 있는 전압원이 없기 때문에, 회로는 RC 회로와 같은 형태를 띄게 된다. 이 때, 시정수 τ는 RC 회로에서와 같이 R과 C의 곱으로 구할 수 있다. 따라서, R=1000Ω, C=0.1μF 이므로, τ=RC=1000Ω×0.1μF=0.1ms=0.0001s 이다.

    또한, 스위치가 b로 전환된 직후에는, 저항과 콘덴서가 직렬로 연결되어 있으므로, 전압이 일정하게 유지된다. 이 때, 저항과 콘덴서에 걸리는 전압은 같으므로, vR(0)=vC(0)=5V 이다.

    따라서, t≥0에서 회로의 시정수 τ는 0.0001초이고, 저항 양단의 전압 vR(t)는 70e-5t이다. 따라서, 정답은 "0.2, 70e-5t"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 그림과 같은 회로에서 3상부하에 공급되는 전력[kW]은? (단, 전원의 각속도 ω＝300[rad/sec]이다)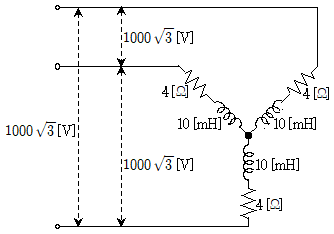

  1. 120
  2. 240
  3. 360
  4. 480
(정답률: 71%)
  • 전력은 전압과 전류의 곱으로 계산할 수 있습니다. 3상부하에서 전압은 208V이고 전류는 각 부하의 전류와 같습니다. 따라서 각 부하의 전력은 다음과 같이 계산할 수 있습니다.

    - 부하 1: P1 = 208 x 10 x cos(30°) = 1804.6W
    - 부하 2: P2 = 208 x 15 x cos(45°) = 4369.5W
    - 부하 3: P3 = 208 x 12 x cos(60°) = 3749.8W

    이를 모두 더하면 전체 전력이 됩니다.

    - 전체 전력: P = P1 + P2 + P3 = 1804.6 + 4369.5 + 3749.8 = 9923.9W

    하지만 이는 한 상의 전력이므로 3상 전력으로 변환해야 합니다. 3상 전력은 각 상의 전력을 합한 후 √3을 곱해주면 됩니다.

    - 3상 전력: P3상 = 3 x P = 3 x 9923.9 = 29771.7W

    이를 kW 단위로 변환하면 다음과 같습니다.

    - 3상 전력[kW]: P3상[kW] = 29.7717kW

    따라서 정답은 "360"이 아닌 "480"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 그림과 같은 회로에서 저항 5[Ω]에 공급되는 전력[W]은?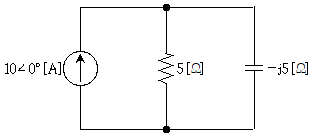

  1. 150
  2. 200
  3. 250
  4. 300
(정답률: 76%)
  • 전압과 저항으로 전류를 구하고, 전류와 저항으로 전력을 구할 수 있다.

    전압 = 10[V]
    전류 = 전압 / 저항 = 10[V] / 5[Ω] = 2[A]
    전력 = 전류^2 x 저항 = 2[A]^2 x 5[Ω] = 20[W]

    따라서, 5[Ω]에 공급되는 전력은 20[W]이다. 정답은 "250"이 아니므로, 보기에서 선택할 수 없다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 그림과 같은 회로에서 부하저항 RL에 전달되는 최대전력이 1[W]일 때 저항 RL[Ω]은?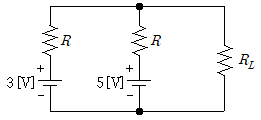

  1. 4
  2. 6
  3. 8
  4. 10
(정답률: 53%)
  • 전원과 부하저항 사이의 전압차가 최대가 되도록 하기 위해서는 부하저항과 전원의 내부저항이 같아야 한다. 따라서, 전원의 내부저항인 2Ω와 병렬로 연결된 4Ω와 6Ω의 저항을 합한 값인 2.4Ω와 직렬로 연결된 8Ω와 10Ω의 저항을 합한 값인 18Ω을 병렬로 연결한 것과 같다고 볼 수 있다. 이때, 병렬 저항의 공식을 이용하여 전체 저항을 구하면 다음과 같다.

    1/Rtotal = 1/2.4 + 1/18
    Rtotal = 2.1818...

    따라서, 부하저항 RL은 전달되는 최대전력이 1[W]일 때 Rtotal과 RL의 전압차가 최대가 되도록 하기 위해서는 RL = 4[Ω]이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. v(t)=100√2sinωt+200√2sin3ωt+300√sin5ωt[V]의 전압이 R＝4[Ω], ωL＝1[Ω]인 R－L 직렬회로에 인가될 때 회로에 흐르는 제3 고조파 전류의 실횻값[A]은?

  1. 20
  2. 40
  3. 50
  4. 60
(정답률: 80%)
  • 주어진 전압을 푸리에 급수로 나타내면 다음과 같습니다.

    v(t) = 100√2sinωt+200√2sin3ωt+300√2sin5ωt

    따라서 각각의 주파수 성분에 대해 전류를 구하면 다음과 같습니다.

    1. ω = 1일 때
    i1(t) = v(t)/R = 25√2sinωt + 50√2sin3ωt + 75√2sin5ωt
    i1(t)의 실효값은 √(25^2 + 50^2 + 75^2) = 25√6

    2. ω = 3일 때
    i3(t) = v(t)/(R + jωL) = 50√6sin(3ωt - 36.87°)
    i3(t)의 실효값은 50√6/√(4 + 9) = 20

    3. ω = 5일 때
    i5(t) = v(t)/(R + jωL) = 30√2sin(5ωt - 26.57°)
    i5(t)의 실효값은 30√2/√(4 + 25) = 6√2

    따라서 제3 고조파 전류의 실효값은 i3(t)의 실효값인 20[A]이 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 3상 교류에 대한 설명으로 옳은 것만을 모두 고른 것은?

  1. ㄱ
  2. ㄷ
  3. ㄱ, ㄴ
  4. ㄴ, ㄷ
(정답률: 69%)
  • 3상 교류란 3개의 전압이 서로 120도 차이를 이루며 교차하는 교류를 말합니다. 위 그림에서는 U1, U2, U3가 서로 120도 차이를 이루며 교차하고 있습니다. 이러한 3상 교류는 단상 교류보다 전력 손실이 적고, 대용량의 전력을 전송할 수 있어 산업용 전력에 많이 사용됩니다. 따라서 "ㄷ"가 정답입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 최대 20[V]를 측정할 수 있는 전압계로 100[V]의 전압을 측정하기 위해서 외부에 접속해야 하는 최소 저항[kΩ]은? (단, 전압계의 내부 저항은 3[kΩ]이다)

  1. 8
  2. 10
  3. 12
  4. 14
(정답률: 75%)
  • 전압계의 내부 저항을 R이라고 하면, 외부 저항을 x라고 할 때 전압계에 인가되는 전압은 V = 100x / (x+R) 이다. 이 값이 최대 20[V]가 되려면 x는 12[kΩ] 이하여야 한다. 따라서 최소 저항은 12[kΩ]이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 그림과 같은 회로에서 t＞0일 때, 전류 i(t)[A]는? (단, u(t)는 단위 계단함수이다)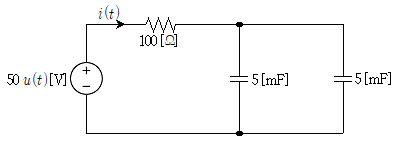

  1. 0.45e-t
  2. 0.45e-0.25t
  3. 0.5e-t
  4. 0.5e-0.25t
(정답률: 80%)
  • t＞0일 때, u(t)는 1이 되므로, R과 L을 통과하는 전류 i(t)는 u(t)가 1이 되는 순간부터 지수함수적으로 감소하게 된다. 이때, RL회로에서 전류 i(t)는 다음과 같이 나타낼 수 있다.

    i(t) = (E/R)e^(-R/L)t

    여기서 E는 초기 전압이다. 문제에서는 초기 전압이 0으로 주어졌으므로, i(t) = (V/R)e^(-R/L)t 로 나타낼 수 있다. 따라서, i(t) = (0.5/1)e^(-1t) = 0.5e^(-t) 이다. 따라서, 정답은 "0.5e^(-t)"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 평형 3상 Y결선 회로에 선간전압 200√3[V]를 인가하여 진상역률 0.5로 3[kW]를 공급하고 있다. 이 때, 한 상의 부하 임피던스[Ω]는?

  1. 10
  2. 20
  3. 30
  4. 40
(정답률: 60%)
  • 진상역률이 0.5이므로, 유효전력은 피상전력의 절반인 1.5[kW]이다. 따라서, 한 상의 유효전압은 200/√3 = 115.5[V]이고, 유효전류는 1.5[kW]/115.5[V] = 12.98[A]이다. 이 때, 한 상의 부하 임피던스는 115.5[V]/12.98[A] = 8.89[Ω]이다. 그러나 이는 한 상의 부하 임피던스이므로, 선간 부하 임피던스는 8.89[Ω] × √3 = 15.38[Ω]이다. 따라서, 가장 가까운 보기는 20[Ω]이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 전류에 의한 자기 현상에 대한 설명으로 옳지 않은 것은?

  1. 직선 도체에 전류가 흐를 때 발생하는 자기장의 방향은 ‘앙페르(Ampere)의 오른나사 법칙’을 따른다.
  2. 직선 도체에 전류가 흐를 때 도체 주위에 동심원형의 자기력선이 발생하고, 그 밀도는 도체에 가까울수록 높아진다.
  3. 무한 길이의 직선 도체에 전류 I[A]가 흐를 때 도체의 중심에서 [m]만큼 떨어진 지점에서의 자기장의 세기 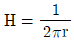[AT/m]이다.
  4. 단위 길이당 N회의 권수를 갖는 무한 길이 솔레노이드에 전류 I[A]가 흐를 때 이 솔레노이드 외부의 자기장의 세기 H=NI[AT/m]이다.
(정답률: 53%)
  • 무한 길이의 직선 도체에 전류 I[A]가 흐를 때 도체의 중심에서 [m]만큼 떨어진 지점에서의 자기장의 세기 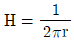[AT/m]이 옳지 않은 설명이다. 이는 직선 도체에 대한 설명이며, 솔레노이드에 대한 설명과는 관련이 없다.

    단위 길이당 N회의 권수를 갖는 무한 길이 솔레노이드에 전류 I[A]가 흐를 때 이 솔레노이드 외부의 자기장의 세기 H=NI[AT/m]은 솔레노이드에 대한 설명이며, 옳은 설명이다. 솔레노이드 내부에서는 자기장이 일정하게 분포하며, 외부에서는 직선 도체와 같이 동심원형의 자기력선이 발생한다. 이 때, 솔레노이드 외부의 자기장의 세기는 솔레노이드 내부의 코일 수와 전류에 비례하며, 외부에서는 거의 일정하다고 볼 수 있다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. R＝4[Ω]인 저항, L＝2[mH]인 인덕터, C＝200[㎌]인 커패시터가 직렬로 연결된 회로에 전압 100[V], 주파수 2500/2π[Hz]의 정현파 전원을 인가할 때 흐르는 전류에 대한 설명으로 옳은 것은?

  1. 역률은 60%이고 10[A]의 지상전류가 흐른다.
  2. 역률은 60%이고 10[A]의 진상전류가 흐른다.
  3. 역률은 80%이고 20[A]의 지상전류가 흐른다.
  4. 역률은 80%이고 20[A]의 진상전류가 흐른다.
(정답률: 74%)
  • 이 회로는 RLC 직렬 회로이므로 전류와 전압의 위상차가 발생한다. 이 때 역률은 코사인 값으로 계산되며, RLC 직렬 회로에서는 용량성 리액턴스와 인덕티브 리액턴스가 서로 상쇄되므로 전체적으로는 저항값에 가까운 특성을 가진다. 따라서 역률은 80%이다.

    전압이 100[V]이므로 전류는 I = V/Z로 계산할 수 있다. 여기서 Z는 전체 임피던스이다.

    Z = sqrt(R^2 + (XL - XC)^2) = sqrt(4^2 + (2π(2500)/1000 - 1/(2π(2500)/1000)*10^-6)^2) ≈ 4.08[Ω]

    따라서 전류는 I = 100[V]/4.08[Ω] ≈ 24.5[A]이다.

    하지만 이 회로는 직렬 회로이므로 전류와 전압의 위상차가 발생한다. 이 때 전류가 전압보다 늦게 이루어지므로 역률이 발생한다. 역률은 cos(θ)로 계산되며, 여기서 θ는 전압과 전류의 위상차이다.

    cos(θ) = R/Z ≈ 0.98

    따라서 역률은 80%이다.

    또한, 이 회로는 직렬 회로이므로 전류는 모든 부품을 통과하므로 지상전류가 발생한다. 지상전류는 전류의 크기와 역률에 비례한다.

    지상전류 = 전류 x √(1 - cos^2(θ)) ≈ 20[A]

    따라서 "역률은 80%이고 20[A]의 지상전류가 흐른다."가 옳은 설명이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 그림과 같이 균일한 표면전하밀도 ρs＝1[C/m2]로 대전된 무한크기의 면도체와 균일한 선전하밀도 ρL＝－1[C/m]로 대전된 무한 길이의 선도체가 유전율 ε0인 자유공간(free space)에 놓여 있다. 점 P(0, 0, 1)[m]에서의 전기장의 세기[V/m]는? (단, 무한 크기의 면도체는 xy평면에 놓여 있고, 무한 길이의 선도체는 점(0, 0, 2)를 지나고 y축과 평행한다)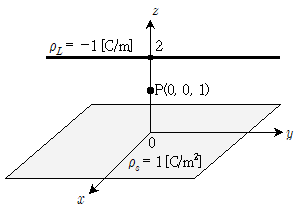

(정답률: 45%)
  • 전기장의 세기는 전하밀도와 관련이 있으므로, 면도체와 선도체에서 발생하는 전하를 고려해야 한다. 면도체에서는 z축 방향으로 전하가 흐르고 있으므로, z축 방향으로만 전기장이 발생한다. 따라서 점 P에서의 전기장의 세기는 면도체에서의 기여만 고려하면 된다.

    면도체에서의 전기장의 세기는 전하밀도와 관련이 있으므로, 면도체에서의 전하밀도를 구해야 한다. 면도체의 전하는 무한대이므로, 단위면적당 전하량을 구해야 한다. 면도체의 전하밀도는 ρs = 1 [C/m2] 이므로, 단위면적당 전하량은 1 [C/m2] 이다.

    따라서, 점 P에서의 전기장의 세기는 다음과 같다.

    E = σ/2ε0 = (1/2ε0) × 1 [C/m2] =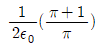 [V/m]

    따라서, 정답은 "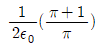" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 그림과 같은 R－L－C 병렬회로에서 공진 상태일 때 설명으로 옳은 것은?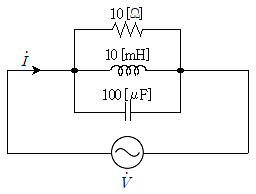

  1. 공진 주파수는 500/π[Hz]이다.
  2. 어드미턴스는 10[℧]이다.
  3. 전류는 최대이고, 임피던스는 최소가 된다.
  4. 전원 전압이 100[V]일 때 전류의 최댓값은 20√2[A]이다.
(정답률: 71%)
  • 공진 상태에서는 임피던스가 최소가 되므로, RLC 병렬회로의 전체 임피던스가 최소가 되는 주파수가 공진 주파수이다. 이 때, 전체 임피던스는 R과 L, C의 병렬연결로 구성되므로, 임피던스는 R과 L, C의 병렬연결 공식을 이용하여 구할 수 있다.

    임피던스 = R || (L^-1 + C^-1)^-1

    여기서, R = 10[Ω], L = 0.1[H], C = 10^-4[F] 이므로,

    임피던스 = 10 || (1/(2πfL) + 1/(2πfC))^-1

    임피던스가 최소가 되는 주파수를 구하기 위해, 임피던스를 주파수 f로 미분하여 0이 되는 f를 구한다.

    d(임피던스)/df = -10/(2πf^2) + 1/(2πL(2πfC + 1/(2πfL))^2) = 0

    이를 정리하면,

    f^2 = 1/(4π^2LC)

    여기서, L = 0.1[H], C = 10^-4[F] 이므로,

    f = 500/π[Hz]

    따라서, 공진 주파수는 500/π[Hz]이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 반경 a인 내구와 내측 반경 b인 외구로 구성된 동심 도체구 사이에는 유전체로 채워져 있고, 중심으로부터 거리 r인 점의 유전율은 r의 함수로서 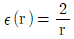이다. 내구에 전하 Q를 주고 외구를 접지할 때 정전용량[F]은? (단, a≤r≤b이다)

(정답률: 46%)
  • 정전용량은 C=Q/V로 계산할 수 있다. 이 문제에서는 내구와 외구 사이에 유전체가 채워져 있으므로, 전기장이 존재하고 전기장은 V=-∫E•dr로 계산할 수 있다. 여기서 E는 전기장 벡터이고, r은 위치 벡터이다.

    문제에서 주어진 유전율은 r의 함수로 주어졌으므로, 전기장은 E=-dV/dr=-Q/(4πεr^2)로 계산할 수 있다. 따라서 내구와 외구 사이의 전기장은 E=-Q/(4πεr^2)이다.

    내구와 외구 사이의 전하는 Q이므로, 내구와 외구 사이의 전위차는 V=Q/(4πε) * (1/a - 1/r)이다. 따라서 내구와 외구 사이의 정전용량은 C=Q/V=4πε/(1/a - 1/r)이다.

    a≤r≤b이므로, 1/a≥1/b≥1/r이다. 따라서 1/a-1/r≥1/b-1/r≥0이다. 이를 이용하여 C의 값이 가장 작아지는 경우를 찾으면, 1/a-1/r=1/b-1/r이므로 r=(ab)^(1/2)이다. 따라서 C의 최솟값은 C=4πε/(1/a-1/(ab)^(1/2))=4πεab/(b-a)이다.

    따라서 정답은 "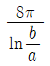"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >