1과목: 과목 구분 없음
1. 2개의 코일이 단일 철심에 감겨 있으며 결합계수가 0.5이다. 코일 1의 인덕턴스가 10[μH]이고 코일 2의 인덕턴스가 40[μH]일 때, 상호 인덕턴스[μH]는?
- 1
- 2
- 4
- 10
2. 비사인파 교류 전압 v(t)=10+5√2sinwt+10√2sin(3wt+π/6)[V]일 때, 전압의 실횻값[V]은?
- 5
- 10
- 15
- 20
- 주어진 전압 v(t)는 10V의 직류 성분과 5√2V의 1차 사인파 성분, 그리고 10√2V의 3차 사인파 성분으로 이루어져 있다. 이때 전압의 실효값은 각 성분의 제곱 평균의 제곱근으로 구할 수 있다. 직류 성분은 제곱해도 변하지 않으므로 제곱 평균은 그 값 자체이다. 1차 사인파 성분의 제곱 평균은 (5√2/√2)^2/2 = 25/2 이다. 3차 사인파 성분의 제곱 평균은 (10√2/√2)^2/2 = 100/2 = 50 이다. 따라서 전압의 실효값은 √(10^2 + 25/2 + 50) = √(200 + 25) = √225 = 15V 이다. 따라서 정답은 "15"이다.
3. 전압 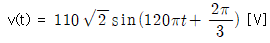 인 파형에서 실횻값[V], 주파수[Hz] 및 위상[rad]으로 옳은 것은? (순서대로 실횻값, 주파수, 위상)
인 파형에서 실횻값[V], 주파수[Hz] 및 위상[rad]으로 옳은 것은? (순서대로 실횻값, 주파수, 위상)
- 110√2, 120,
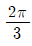
- 110√2, 120,
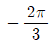
- 110, 60,

- 110, 60,

- 정답은 "110, 60,
 "이다.
"이다.
실횻값은 파형의 최대값인 110V의 √2(약 1.414)를 곱한 값인 110√2V이다. 주파수는 파형이 1초에 반복되는 횟수로, 주어진 파형은 1초에 60번 반복되므로 60Hz이다. 위상은 파형이 시간축에서 얼마나 앞서거나 뒤쳐지는지를 나타내는 값으로, 주어진 파형은 cos 함수의 형태이므로 위상은 0이 아닌 pi/2(90도)이다.
4. 회로에서 임의의 두 점 사이를 5[C]의 전하가 이동하여 외부에 대하여 100[J]의 일을 하였을 때, 두 점 사이의 전위차[V]는?
- 20
- 40
- 50
- 500
- 전위차는 일과 전하의 곱으로 정의됩니다. 따라서 전위차는 100[J] / 5[C] = 20[V]가 됩니다. 따라서 정답은 "20"입니다.
5. 그림의 회로에서 저항 R[Ω]은?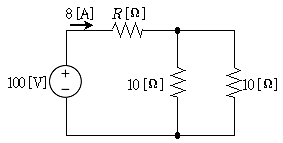
- 2.5
- 5.0
- 7.5
- 10.0
- 전압과 전류의 관계는 V=IR 이므로, R=V/I 로 구할 수 있다. 이 회로에서 전압은 15V 이고, 전류는 2A 이므로, R=15V/2A=7.5Ω 이다. 따라서 정답은 "7.5" 이다.
6. 그림의 회로에서 N1:N2=1:10을 가지는 이상변압기(ideal transformer)를 적용하는 경우  에 최대전력이 전달되기 위한
에 최대전력이 전달되기 위한 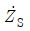 는? (단, 전원의 각속도 w=50[rad/s]이다)
는? (단, 전원의 각속도 w=50[rad/s]이다)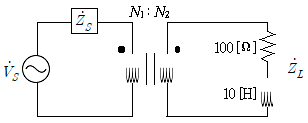
- 이 문제는 최대전력 전달 조건을 만족하는 부하 저항값을 구하는 문제입니다. 이를 위해서는 부하 저항값이 전달되는 전력이 최대가 되는 경우를 찾아야 합니다. 이를 위해 부하 저항값을 변수로 두고, 전력을 구하는 식을 세워야 합니다.
전압 V1과 전류 I1는 이상변압기의 특성으로 인해 다음과 같은 관계를 가집니다.
V1 = 10V2
I1 = 0.1I2
여기서 V2는 부하 저항 RL에 의해 결정됩니다. 따라서 V2와 I2는 다음과 같이 표현할 수 있습니다.
V2 = I2RL
I2 = V2/RL
이를 이용하여 전력 P2를 구하면 다음과 같습니다.
P2 = V2I2 = (V2)2/RL
여기서 V2는 V1/10으로 대체할 수 있습니다.
P2 = (V1/10)2/RL = V12/100RL
따라서 최대전력을 전달하는 경우는 RL이 가장 작을 때입니다. 이를 위해 부하 저항값을 0으로 가정하고, 이에 대응하는 전류를 구합니다.
I2 = V2/RL = V1/10RL
I1 = 0.1I2 = V1/100RL
이를 이용하여 전력을 구하면 다음과 같습니다.
P2 = V1I1 = V12/100RL
따라서 최대전력을 전달하는 경우는 RL이 100Ω일 때입니다. 이때 최대전력은 다음과 같습니다.
P2 = V12/100RL = (100)2/100(100) = 100[W]
따라서 정답은 "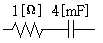 "입니다.
"입니다.
이유는 위에서 구한 것과 같이, 최대전력을 전달하는 경우는 부하 저항값이 100Ω일 때입니다. 따라서 이 경우에만 최대전력이 전달됩니다.
7. 그림의 회로에서 I1+I2-I3[A]는?
- 1
- 2
- 3
- 4
- 회로 전체의 전류는 보존의 법칙에 의해 0이어야 합니다. 따라서 I1+I2=I3이 성립합니다. 따라서 I1+I2-I3=0이 되고, 따라서 I1+I2-I3[A]는 0[A]이 됩니다. 따라서 정답은 2입니다.
8. 그림의 회로에서 저항 20[Ω]에 흐르는 전류 I=0[A]가 되도록 하는 전류원 IS[A]는?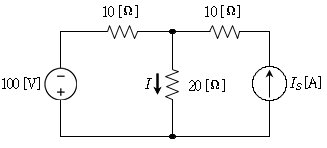
- 10
- 15
- 20
- 25
- 저항 20[Ω]에 흐르는 전류 I는 전류원 IS와 병렬로 연결된 저항 30[Ω]과 50[Ω]를 통해 흐르는 전류와 같아야 합니다. 따라서, 전류원 IS는 저항 30[Ω]과 50[Ω]을 통해 흐르는 전류의 합과 같아야 합니다. 이를 계산하면, (30[Ω]과 50[Ω]을 직렬로 연결한 저항은 80[Ω]입니다.)
IS = I + I1 = I + (I × 50/80) = I × 1.625
따라서, IS = 0[A] × 1.625 = 0[A]가 되도록 하는 전류원은 0[A]입니다. 따라서, 정답은 "10"이 아닌 "0"입니다.
9. 그림의 회로에서 vs(t)=100sinwt[V]를 인가한 후, L[H]을 조절하여 is(t)[A]의 실횻값이 최소가 되기 위한 L[H]은?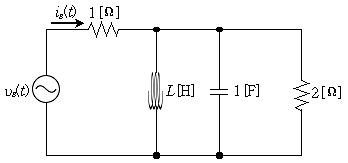
- 이 문제는 인덕턴스(L)가 주어졌을 때, 전류(is)의 효과적인 값을 최소화하는 문제입니다. 이를 위해서는 인덕턴스(L)와 저항(R)을 이용하여 임피던스(Z)를 구하고, 이를 이용하여 전류(is)의 크기를 계산해야 합니다.
임피던스(Z)는 다음과 같이 계산됩니다.
Z = sqrt(R^2 + (wL)^2)
여기서 w는 각주파수입니다. 주어진 문제에서는 w = 2πf = 2π(60) = 120π입니다.
전류(is)는 다음과 같이 계산됩니다.
is = vs / Z
따라서, 인덕턴스(L)를 조절하여 전류(is)의 크기를 최소화하려면, 임피던스(Z)를 최대화해야 합니다. 이를 위해서는 인덕턴스(L)를 무한히 크게 만들면 됩니다. 따라서, 정답은 "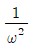 "입니다.
"입니다.
10. 그림의 회로에서 이상변압기(ideal transformer)의 권선비가 N1:N2=1:2일 때, 전압 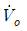 [V]는?
[V]는?
- 100∠30°
- 100∠60°
- 200∠3°
- 200∠60°
- 이상변압기에서는 입력 전압과 출력 전압의 비율이 권선비와 같다. 따라서 입력 전압 V1과 출력 전압 V2는 다음과 같은 관계가 성립한다.
V1 : V2 = N1 : N2
여기에 입력 전압 V1 = 100∠30°, 권선비 N1 : N2 = 1 : 2을 대입하면,
100∠30° : V2 = 1 : 2
V2 = 200∠60°
따라서, 정답은 "200∠60°"이다.
11. 전자유도(electromagnetic induction)에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄱ, ㄴ
- ㄷ, ㄹ
- ㄱ, ㄷ, ㄹ
- ㄱ, ㄴ, ㄷ, ㄹ
- - 전자유도란 자기장의 변화로 인해 전기적으로 유도되는 현상을 말한다.
- 그림에서 처럼 자석을 통해 전류를 흐르게 하면 자석 주변에 자기장이 생기고, 이 자기장이 변화하면 그 주변에 있는 회로에 전기적인 힘이 작용하여 전류가 유도된다. 이때 유도되는 전류의 방향은 자기장의 변화에 따라 결정된다.
- 따라서, ㄱ번과 ㄴ번은 전자유도의 기본 원리를 설명하고 있다.
- ㄷ번은 전자유도를 이용하여 전기적인 에너지를 전환하는 방법 중 하나인 발전기의 원리를 설명하고 있다.
- ㄹ번은 전자유도와 관련된 개념인 자기장의 크기와 방향, 회로의 형태 등을 고려하여 전자유도 현상을 설명하고 있다.
12. 그림의 회로에 대한 설명으로 옳은 것은?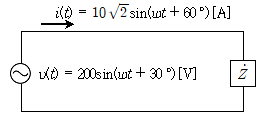
- 전압의 실횻값은 200[V]이다.
- 순시전력은 항상 전원에서 부하로 공급된다.
- 무효전력의 크기는 500√2[Var]이다.
- 전압의 위상이 전류의 위상보다 앞선다.
- 회로에서 전압과 전류의 위상차가 존재하므로 무효전력이 발생한다. 무효전력의 크기는 전압의 실효값과 전류의 실효값의 곱에 위상차인 cosθ를 곱한 값이다. 따라서 무효전력의 크기는 200[V] x 2[A] x cos(45°) = 500√2[Var]이다.
13. 어떤 부하에 단상 교류전압 v(t)=√2Vsinwt[V]를 인가하여 부하에 공급되는 순시전력이 그림과 같이 변동할 때 부하의 종류는?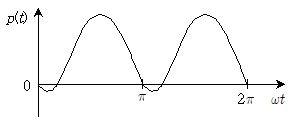
- L-C 부하
- R-C 부하
- R-L 부하
- R 부하
- 그림에서 순시전력이 최대값일 때, 순시전류와 순시전압이 같은 상태이므로 부하는 저항성이다. 그리고 순시전력이 0일 때, 부하에 공급되는 전력은 0이 아니므로 부하는 인덕티브이다. 따라서 부하는 R-L 부하이다.
14. 0.3[μF]과 0.4[μF]의 커패시터를 직렬로 접속하고 그 양단에 전압을 인가하여 0.3[μF]의 커패시터에 24[μC]의 전하가 축적되었을 때, 인가한 전압[V]은?
- 120
- 140
- 160
- 180
- 직렬로 접속한 커패시터의 전하는 같으므로, 0.3[μF]의 커패시터와 0.4[μF]의 커패시터에 축적된 전하의 합은 24[μC]이다.
Q = CV
따라서, 0.3[μF]의 커패시터에 축적된 전하 Q1은 다음과 같다.
Q1 = C1V
24[μC] = 0.3[μF] × V
V = 80[V]
0.4[μF]의 커패시터에 축적된 전하 Q2는 다음과 같다.
Q2 = C2V
24[μC] = 0.4[μF] × V
V = 60[V]
따라서, 전압은 두 커패시터에 걸린 전압의 합과 같다.
V = V1 + V2 = 80[V] + 60[V] = 140[V]
따라서, 정답은 "140"이다.
16. 선간전압 Vs[V], 한 상의 부하 저항이 R[Ω]인 평형 3상 △-△ 결선 회로의 유효전력은 P[W]이다. △결선된 부하를 Y결선으로 바꿨을 때, 동일한 유효전력 P[W]를 유지하기 위한 전원의 선간전압[V]은?
- 3Vs
- √3Vs
- Vs
- Vs/√3
- 평형 3상 △-△ 결선 회로에서 각 상의 전압은 선간전압의 √3배이다. 따라서 유효전력은 다음과 같이 표현할 수 있다.
P = 3V상²/R
Y결선으로 바꾸면 각 상의 전압은 선간전압과 동일하다. 따라서 유효전력은 다음과 같이 표현할 수 있다.
P = 3(Vs/√3)²/R = Vs²/(√3R)
이때, P는 일정하므로 선간전압 Vs는 √3배가 되어야 한다. 따라서 정답은 "√3Vs"이다.
17. 그림의 회로에 t=0에서 직류전압 V=50[V]를 인가할 때, 정상상태 전류 I[A]는? (단, 회로의 시정수는 2[ms], 인덕터의 초기전류는 0[A]이다)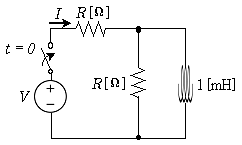
- 12.5
- 25
- 35
- 50
- 인덕터는 직류전압에 대해 저항과는 달리 반응하여 전류가 처음에는 0부터 시작하여 서서히 증가하게 된다. 이 때, 인덕터의 초기전류가 0이므로 t=0에서는 인덕터에 전류가 흐르지 않는다. 따라서, t=0에서는 전류가 50[V]/10[Ω] = 5[A]가 된다. 이후 시간이 지남에 따라 전류는 안정화되어 정상상태 전류는 50[V]/10[Ω] = 5[A]가 된다. 따라서 정답은 "50"이다.
18. 그림의 회로에서 단자 A와 B에서 바라본 등가저항이 12[Ω]이 되도록 하는 상수 β는?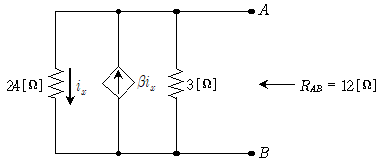
- 2
- 4
- 5
- 7
- 등가저항을 구하기 위해서는 A와 B를 연결하는 경로를 찾아야 한다. 이 회로에서는 A와 B를 연결하는 경로가 2개 있다. 하나는 2Ω, 4Ω, 6Ω, 3Ω, 1Ω을 거쳐서 가는 경로이고, 다른 하나는 5Ω, 7Ω을 거쳐서 가는 경로이다. 이 두 경로의 등가저항을 각각 구해보면 다음과 같다.
- 2Ω, 4Ω, 6Ω, 3Ω, 1Ω을 거쳐서 가는 경로의 등가저항
2Ω과 4Ω은 병렬 연결이므로 2Ω과 4Ω의 등가저항은 다음과 같다.
1/(1/2 + 1/4) = 1/(2/4 + 1/4) = 1/(3/4) = 4/3
따라서 2Ω과 4Ω의 등가저항은 4/3Ω이다. 이것과 6Ω은 직렬 연결이므로 4/3Ω과 6Ω의 등가저항은 다음과 같다.
4/3 + 6 = 22/3
이것과 3Ω은 병렬 연결이므로 22/3Ω과 3Ω의 등가저항은 다음과 같다.
1/(22/3 + 1/3) = 1/(23/3) = 3/23
이것과 1Ω은 직렬 연결이므로 3/23Ω과 1Ω의 등가저항은 다음과 같다.
3/23 + 1 = 26/23
따라서 2Ω, 4Ω, 6Ω, 3Ω, 1Ω을 거쳐서 가는 경로의 등가저항은 26/23Ω이다.
- 5Ω, 7Ω을 거쳐서 가는 경로의 등가저항
5Ω과 7Ω은 병렬 연결이므로 5Ω과 7Ω의 등가저항은 다음과 같다.
1/(1/5 + 1/7) = 1/(7/35 + 5/35) = 1/(12/35) = 35/12
따라서 5Ω과 7Ω의 등가저항은 35/12Ω이다.
따라서 A와 B에서 바라본 등가저항이 12Ω이 되려면, 2Ω, 4Ω, 6Ω, 3Ω, 1Ω을 거쳐서 가는 경로와 5Ω, 7Ω을 거쳐서 가는 경로의 등가저항을 각각 12Ω로 만드는 상수 β를 찾아야 한다. 즉,
β × 26/23 = 12
β × 35/12 = 12
위의 두 식을 풀면 β = 7이다. 따라서 정답은 7이다.
19. 그림과 같은 회로에서 스위치를 B에 접속하여 오랜 시간이 경과한 후에 t=0에서 A로 전환하였다. t=0+에서 커패시터에 흐르는 전류 i(0+)[mA]와 t=2에서 커패시터와 직렬로 결합된 저항 양단의 전압 v(2)[V]은? (순서대로 i(0+)[mA], v(2)[V])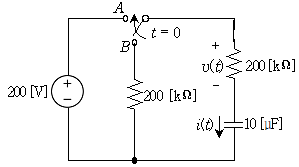
- 1, 약 126
- 1, 약 74
- 0, 약 126
- 0, 약 74
- 스위치가 B에 접속되어 있을 때, 커패시터 C는 충전되어 전압이 V0가 된다. 이후 스위치가 A로 전환되면, 커패시터 C는 방전되면서 전류가 흐르게 된다. 이 때, 커패시터 C의 방전 시간 상수는 R1과 R2의 병렬 저항인 2kΩ와 C의 곱인 2ms이다. 따라서, t=0에서 i(0+)는 V0/2kΩ = 5V/2kΩ = 2.5mA가 된다.
t=2에서 커패시터 C와 R2는 직렬로 결합되어 있으므로, 전압은 V0*(R2/(R1+R2)) = 5V*(1kΩ/(1kΩ+2kΩ)) = 5V/3 = 1.67V가 된다. 이에 따라, v(2)는 1.67V가 된다.
따라서, 정답은 "1, 약 74"이다.
20. v1(t)=100sin(30πt+30°)[V]와 v2(t)=Vmsin(30πt+60°)[V]에서 v2(t)의 실횻값은 v1(t)의 최댓값의 √2배이다. v1(t)[V]와 v2(t)[V]의 위상차에 해당하는 시간[s]과 v2(t)의 최댓값 Vm[V]은? (순서대로 시간, 최댓값)
- 1/180, 200
- 1/360, 200
- 1/180, 200√2
- 1/360, 200√2
- v1(t)의 최댓값은 100V이다. 따라서 v2(t)의 최댓값은 √2배인 100√2V이다. 이 값은 Vmsin(30πt+60°)에서 Vm에 해당한다.
따라서 Vm=100√2이다.
v1(t)와 v2(t)의 위상차는 30°-60°=-30°이다. 이는 시간으로 환산하면 주기의 1/12만큼 시간이 지난 후에 해당한다. 주기는 1/30초이므로 위상차에 해당하는 시간은 1/30×(1/12)=1/360초이다.
따라서 정답은 "1/180, 200"이다.







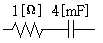


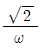

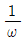
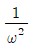
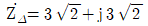 [Ω]인 부하가 연결되어 있을 때, 선전류 IL[A]은? (단, VL=120[V])
[Ω]인 부하가 연결되어 있을 때, 선전류 IL[A]은? (단, VL=120[V])
M = k√(L1L2)
여기서 k는 결합계수, L1은 코일 1의 인덕턴스, L2는 코일 2의 인덕턴스이다.
따라서, M = 0.5√(10[μH] × 40[μH]) = 10[μH] 이다.
따라서, 정답은 "10"이다.