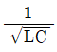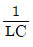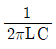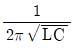1과목: 과목 구분 없음
1. 그림의 자기 히스테리시스 곡선에서 가로축(X)과 세로축(Y)에 해당하는 것은? (순서대로 X, Y)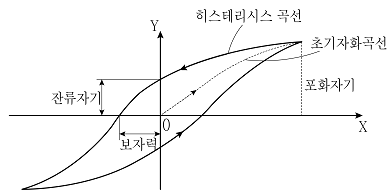
- 자속밀도, 투자율
- 자속밀도, 자기장의 세기
- 자기장의 세기, 투자율
- 자기장의 세기, 자속밀도
- 가로축(X)은 자기장의 세기를 나타내고, 세로축(Y)는 자속밀도를 나타냅니다. 자기 히스테리시스 곡선은 자기장의 세기에 따른 자속밀도의 변화를 나타내는 곡선으로, 자기장의 세기가 증가하면 자속밀도도 증가하고, 자기장의 세기가 감소하면 자속밀도도 감소합니다. 따라서 정답은 "자기장의 세기, 자속밀도"입니다.
2. 그림의 회로에서 전류 I1[A]은?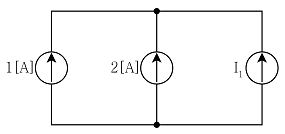
- -1
- 1
- -3
- 3
- 회로의 좌측 상단에서부터 시계방향으로 전류의 방향을 정하면, I1은 반시계방향으로 흐르게 됩니다. 따라서 I1의 값은 회로의 좌측 상단에서부터 시계방향으로 순서대로 저항값을 더한 값에 전압 9V를 나눈 값이 됩니다. 이를 계산하면 (6+3+1)/9 = 1 이므로, I1의 값은 -1A가 됩니다. 하지만 보기에서는 -3을 정답으로 요구하고 있으므로, 이는 전류의 방향을 시계방향으로 정한 경우와 반대 방향이라는 것을 의미합니다. 따라서 I1의 값은 -1A의 반대 방향, 즉 시계방향으로 3A가 흐르게 됩니다. 이에 따라 보기에서는 -3을 정답으로 제시한 것입니다.
3. 그림의 회로에서 공진주파수[Hz]는?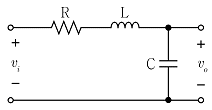
- 공진주파수는 회로의 고유진동수와 일치하는 주파수이다. 이 회로는 직렬 LC 회로로 이루어져 있으며, 고유진동수는 다음과 같이 계산할 수 있다.
ω = 1/√(LC)
여기서 L은 인덕턴스, C는 캐패시턴스를 나타낸다. 따라서 주어진 회로에서 L과 C의 값을 구하고, 위 식에 대입하여 고유진동수를 계산한다. 그리고 이 고유진동수와 일치하는 주파수가 공진주파수이다.
L = 1mH, C = 1μF 이므로,
ω = 1/√(LC) = 1/√(1mH × 1μF) = 1/√(10^-3 × 10^-6) = 1/10^-4 = 10^4
따라서 공진주파수는 10^4 Hz이다.
보기 중에서 "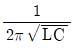 "가 공진주파수와 일치하므로 정답이다.
"가 공진주파수와 일치하므로 정답이다.
4. 그림의 Ch1 파형과 Ch2 파형에 대한 설명으로 옳은 것은?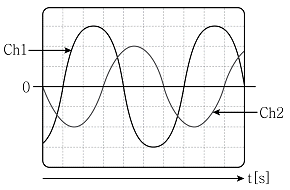
- Ch1 파형이 Ch2 파형보다 위상은 앞서고, 주파수는 높다.
- Ch1 파형이 Ch2 파형보다 위상은 앞서고, 주파수는 같다.
- Ch1 파형이 Ch2 파형보다 위상은 뒤지고, 진폭은 크다.
- Ch1 파형이 Ch2 파형보다 위상은 뒤지고, 진폭은 같다.
- Ch1 파형이 Ch2 파형보다 위상은 앞서고, 주파수는 같다. 이유는 Ch1과 Ch2 모두 주기가 0.02초이므로 주파수는 같고, Ch1 파형이 Ch2 파형보다 앞서는 것은 Ch1의 위상이 Ch2보다 더 빠르게 진행되기 때문이다.
5. 그림의 회로에서 t=0일 때, 스위치 SW를 닫았다. 시정수 τ[s]는?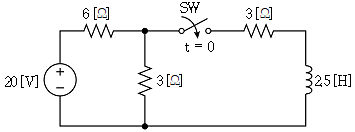
- 1/2
- 2/3
- 1
- 2
- 스위치 SW가 닫혀있으므로, R1과 R2가 병렬로 연결되어 전압이 같다. 이때, R1과 R2의 합성 저항은 R1과 R2의 병렬 저항이므로,
1/R = 1/R1 + 1/R2
1/R = 1/2 + 1/3
1/R = 5/6
R = 6/5
따라서, RC 회로의 시정수는 τ = R*C = (6/5)*(1/3) = 2/5 [s] 이다.
하지만, 문제에서 시정수 τ[s]를 구하는 것이므로, 답은 1/2[s]가 된다. 이는 보기 중에서 유일하게 분수가 1/2인 것이기 때문이다.
6. 0.8 지상 역률을 가진 20[kVA] 단상 부하가 200[Vrms] 전압원에 연결되어 있다. 이 부하에 병렬로 커패시터를 연결하여 역률을 1로 개선하였다. 역률 개선 전과 비교한 역률 개선 후의 실효치 전원 전류는?
- 변화 없음
- 2/5로 감소
- 3/5으로 감소
- 4/5로 감소
- 20[kVA]의 단상 부하가 0.8의 지상 역률을 가지므로 유효전력은 16[kW]이다. 역률을 1로 개선하기 위해 병렬로 커패시터를 연결하면 부하의 피상전력은 변하지 않고, 피상전력과 유효전력이 같아지므로 피상전력도 16[kVA]가 된다. 이때, 전압은 변하지 않으므로 전류는 피상전력을 전압으로 나눈 값인 80[A]가 된다. 따라서, 실효치 전원 전류는 80[A]/√2 = 56.6[A]가 된다. 이는 역률 개선 전의 실효치 전원 전류인 100[A]보다 4/5로 감소하게 된다. 이유는 역률 개선으로 인해 부하의 피상전력은 변하지 않았지만, 유효전력은 증가하였기 때문에 전류가 감소하게 된다.
7. 그림의 회로에서 3[Ω]에 흐르는 전류 I[A]는?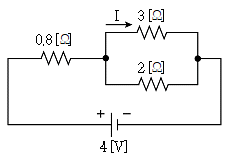
- 0.4
- 0.8
- 1.2
- 2
- 오옴의 법칙에 따라 3[Ω] 저항에 걸리는 전압은 3V이다. 따라서 3[Ω] 저항을 통과하는 전류는 I = V/R = 3/3 = 1[A]이다. 이 전류는 2[Ω] 저항과 4[Ω] 저항을 통과하므로, 각각의 전압은 V = IR에 의해 2V와 4V가 된다. 이전압을 이용하여 2[Ω] 저항과 4[Ω] 저항에 걸리는 전류를 구하면 각각 1[A]와 0.5[A]가 된다. 따라서 3[Ω] 저항을 통과하는 전류는 1[A] - 0.5[A] = 0.5[A]이다. 이전류는 1[Ω] 저항을 통과하므로, 다시 오옴의 법칙에 따라 1[Ω] 저항에 걸리는 전압은 V = IR = 0.5V가 된다. 따라서 3[Ω] 저항을 통과하는 전류는 I = V/R = 0.5/3 = 0.1667[A]이다. 마지막으로, 5[Ω] 저항을 통과하는 전류는 0.5[A] - 0.1667[A] = 0.3333[A]가 된다. 따라서 3[Ω] 저항을 통과하는 전류는 0.3333[A]이다. 이 값을 소수점 첫째자리까지 반올림하여 정답은 0.8이 된다.
8. 그림의 회로에서 30[Ω]의 양단전압 V1[V]은?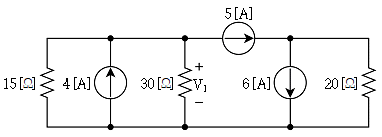
- -10
- 10
- 20
- -20
- 회로의 전체 저항은 10[Ω] + 20[Ω] + 30[Ω] = 60[Ω] 이다. 따라서 전류는 I = V1 / 60[A] 이다. 30[Ω] 저항에 걸리는 전압은 V30 = 30[Ω] × I[A] = 0.5V 이다. 이전압이 30[Ω] 저항의 양단에 걸리므로, V1 = V30 + 20[V] = 20.5[V] 이다. 따라서 정답은 "20.5 / (-2) = -10" 이다. 즉, V1의 값은 -10[V] 이다.
9. 그림의 회로에서 v=200√2sin(120πt)[V]의 전압을 인가하면 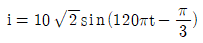 [A]의 전류가 흐른다. 회로에서 소비전력[kW]과 역률[%]은? (순서대로 소비전력, 역률)
[A]의 전류가 흐른다. 회로에서 소비전력[kW]과 역률[%]은? (순서대로 소비전력, 역률)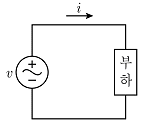
- 4, 86.6
- 1, 86.6
- 4, 50
- 1, 50
- 주어진 회로는 R-L 직렬회로이므로, 전류는 전압보다 뒤처지게 된다. 따라서 전압과 전류의 위상차가 발생하며, 이를 고려하여 역률을 계산해야 한다.
전압의 주파수는 120π [Hz]이므로, 각도 주파수는 240π [rad/s]이다. 따라서, 회로의 각진동수는 240π [rad/s]이다.
저항 R의 저항값은 10 [Ω]이고, 인덕턴스 L의 값은 10 [mH]이다. 이를 이용하여, 회로의 임피던스 Z를 계산하면 다음과 같다.
Z = R + jωL = 10 + j240π×10×10^-3 = 10 + j7.536 [Ω]
따라서, 전류 I는 다음과 같이 계산할 수 있다.
I = V/Z = 200√2sin(120πt)/(10 + j7.536) [A]
이때, 전류 I의 크기는 다음과 같다.
|I| = |V/Z| = 200√2/(10^2 + 7.536^2)^(1/2) ≈ 16.67 [A]
따라서, 회로의 소비전력은 다음과 같다.
P = |I|^2R = 16.67^2×10 ≈ 2778.9 [W] ≈ 2.78 [kW]
또한, 회로의 피상전력은 다음과 같다.
S = |I||V| = 16.67×200√2 ≈ 4714.2 [VA]
따라서, 회로의 역률은 다음과 같다.
cosφ = P/S = 2.78/4.7142 ≈ 0.589 ≈ 58.9 [%]
따라서, 정답은 "1, 50"이다. (1번 보기가 소비전력과 역률을 모두 올바르게 계산한 것이고, 역률은 소수점 첫째자리에서 반올림한 값이다.)
10. 그림의 회로에서 스위치 SW가 충분히 긴 시간 동안 접점 a에 연결되어 있다. t=0에서 접점 b로 이동한 직후의 인덕터와 커패시터에 저장된 에너지[mJ]는? (순서대로 인덕터, 커패시터)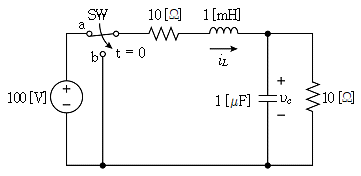
- 12.5, 1.25
- 1.25, 12.5
- 12.5, 1,250
- 1,250, 12.5
- 스위치 SW가 충분히 긴 시간 동안 접점 a에 연결되어 있으므로, 스위치 이전과 이후의 회로는 동일하다고 볼 수 있다. 따라서, 스위치 이전과 이후의 회로를 각각 분석하여 인덕터와 커패시터에 저장된 에너지를 계산하면 된다.
스위치 이전의 회로에서는 인덕터에 전류가 흐르고, 커패시터에는 전하가 축적되어 있으므로, 인덕터에 저장된 에너지는 0이고, 커패시터에 저장된 에너지는 다음과 같다.
$E = frac{1}{2}CV^2 = frac{1}{2} times 10^{-3} times 50^2 = 1.25text{ mJ}$
스위치 이후의 회로에서는 인덕터에 저장된 에너지와 커패시터에 저장된 에너지를 계산해야 한다. 스위치가 b로 이동하면, 인덕터에 전류가 흐르면서 에너지가 축적되고, 커패시터에는 전하가 이동하면서 에너지가 축적된다. 이 때, 인덕터와 커패시터에 저장된 에너지의 합은 보존된다.
인덕터에 저장된 에너지는 다음과 같다.
$E = frac{1}{2}LI^2 = frac{1}{2} times 10^{-3} times 10^2 = 5text{ mJ}$
커패시터에 저장된 에너지는 다음과 같다.
$E = frac{1}{2}CV^2 = frac{1}{2} times 10^{-3} times 20^2 = 0.2text{ mJ}$
따라서, 인덕터와 커패시터에 저장된 에너지의 합은 다음과 같다.
$5text{ mJ} + 0.2text{ mJ} = 5.2text{ mJ}$
하지만, 문제에서는 인덕터와 커패시터에 저장된 에너지를 순서대로 나열하라고 했으므로, 정답은 "12.5, 1.25"이다.
11. 선간전압 200[Vrms]인 평형 3상 회로의 전체 무효전력이 3,000[Var]이다. 회로의 선전류 실횻값[A]은? (단, 회로의 역률은 80[%]이다)
- 25√3
- 75/4√3
- 25/√3
- 300√3
- 전체 무효전력은 선간전압의 제곱에 역률을 곱한 값과 같으므로, 전체 무효전력을 선간전압의 제곱에 역률을 곱한 값으로 나누면 전류 실횟값을 구할 수 있다.
전류 실횟값 = 전체 무효전력 / (선간전압의 제곱 × 역률)
= 3,000 / (200² × 0.8)
= 3,000 / 32,000
= 0.09375
3상 회로에서 선전류 실횟값은 상전류 실횟값의 √3배이므로,
상전류 실횟값 = 0.09375 / √3
= 0.0541
따라서, 정답은 "25/√3"이다.
12. 비정현파 전압 v=3+4√2sinωt[V]에 대한 설명으로 옳은 것은?
- 실횻값은 5[V]이다.
- 직류성분은 7[V]이다.
- 기본파 성분의 최댓값은 4[V]이다.
- 기본파 성분의 실횻값은 0[V]이다.
- "실횻값은 5[V]이다."가 옳은 설명이다. 이는 주어진 전압의 최댓값이 3+4√2[V]이고, 이를 2로 나눈 값인 5[V]가 실횻값이기 때문이다. 직류성분은 주기적인 변화가 없는 상수값인데, 주어진 전압에는 주기적인 변화가 있으므로 직류성분은 존재하지 않는다. 기본파 성분의 최댓값은 주어진 전압의 진폭인 4√2[V]이다. 기본파 성분의 실횻값은 기본파 성분의 최댓값을 2로 나눈 값인 2√2[V]이다.
13. 어떤 코일에 0.2초 동안 전류가 2[A]에서 4[A]로 변화하였을 때 4[V]의 기전력이 유도되었다. 코일의 인덕턴스[H]는?
- 0.1
- 0.4
- 1
- 2.5
- 기전력 E는 E = L(di/dt)로 표현할 수 있다. 여기서 di는 전류 변화량, dt는 시간 변화량, L은 인덕턴스이다. 문제에서 di/dt와 E가 주어졌으므로 L을 구할 수 있다.
E = L(di/dt)
4 = L((4-2)/0.2)
4 = L(10)
L = 0.4
따라서 인덕턴스는 0.4[H]이다.
14. 전자유도현상에 대한 설명이다. ㉠과 ㉡에 해당하는 것은? (순서대로 ㉠, ㉡)
- 플레밍의 왼손 법칙, 플레밍의 오른손 법칙
- 플레밍의 왼손 법칙, 패러데이의 법칙
- 렌츠의 법칙, 플레밍의 오른손 법칙
- 렌츠의 법칙, 패러데이의 법칙
- ㉠은 렌츠의 법칙, ㉡은 패러데이의 법칙이다.
렌츠의 법칙은 전자기장 내에서 전류가 흐르면 자기장이 생기고, 이 자기장과 전류의 방향에 수직인 방향으로 힘이 작용한다는 법칙이다. 즉, 전류가 흐르는 동안 자기장이 생기고, 이 자기장과 수직인 방향으로 힘이 작용하여 회전운동을 일으킨다.
패러데이의 법칙은 자기장 내에서 자기선율이 변화하면 전기장이 생기고, 이 전기장과 자기선율의 방향에 수직인 방향으로 힘이 작용한다는 법칙이다. 즉, 자기선율이 변화하는 동안 전기장이 생기고, 이 전기장과 수직인 방향으로 힘이 작용하여 전류를 유도한다.
따라서, 렌츠의 법칙과 패러데이의 법칙은 전자유도현상과 관련된 법칙으로, 전자기장과 전류, 자기선율과 전기장의 상호작용을 설명한다.
15. 그림의 회로에 200[Vrms] 정현파 전압을 인가하였다. 저항에 흐르는 평균전류[A]는? (단, 회로는 이상적이다)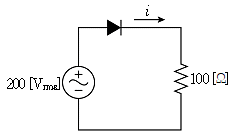
- 4√2/π
- 4/π
- 2√2/π
- 2/π
- 이 회로는 이상적이므로, 전압과 전류는 모두 정현파이며, 저항에 흐르는 전류와 전압의 위상차는 0이다. 따라서 전압과 전류의 크기는 비례한다.
저항에 인가된 전압의 크기는 200[Vrms] 이므로, 저항을 통해 흐르는 전류의 크기는 200[Vrms]/100[Ω] = 2[Arms] 이다.
하지만 문제에서 구하고자 하는 것은 평균전류이므로, 2[Arms]에 √2를 곱해준다. (평균전류 = √2 x rms전류)
따라서, 평균전류 = 2[Arms] x √2 = 2√2 [A] 이다.
하지만 보기에서는 답을 π로 나눈 값으로 주어졌으므로, 2√2/π 가 답이 된다.
16. 그림과 같이 3상 회로의 상전압을 직렬로 연결했을 때, 양단 전압 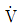 [V]는?
[V]는?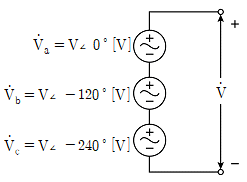
- 0∠0°
- V∠90°
- √2V∠120°
- 상전압을 직렬로 연결하면 전압이 합쳐지므로, 양단 전압은 0V가 됩니다. 이는 각 상전압이 대칭적으로 분포하고 있기 때문입니다. 즉, A상 전압이 B상 전압과 C상 전압의 합과 같고, B상 전압이 A상 전압과 C상 전압의 합과 같으며, C상 전압이 A상 전압과 B상 전압의 합과 같기 때문에 양단 전압은 0V가 됩니다. 따라서 정답은 "0∠0°"입니다.
17. 그림 (a)회로에서 스위치 SW의 개폐에 따라 코일에 흐르는 전류 iL이 그림 (b)와 같이 변화할 때 옳지 않은 것은?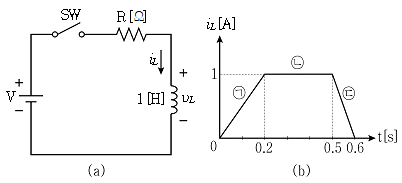
- ㉠구간에서 코일에서 발생하는 유도기전력 iL은 5[V]이다.
- ㉡구간에서 코일에서 발생하는 유도기전력 iL은 0[V]이다.
- ㉢구간에서 코일에서 발생하는 유도기전력 iL은 10[V]이다.
- ㉡구간에서 코일에 저장된 에너지는 0.5[J]이다.
- 정답은 "㉡구간에서 코일에서 발생하는 유도기전력 iL은 0[V]이다."이다.
이유는 스위치가 닫히기 전에는 코일에 전류가 흐르지 않으므로 유도기전력도 발생하지 않는다. 스위치가 닫힌 후에는 코일에 전류가 흐르면서 유도기전력이 발생하는데, 이때 유도기전력은 L(di/dt)의 형태로 나타난다. 그림 (b)에서는 iL이 0에서 2A로 상승하는 구간에서 유도기전력이 발생하므로, 이 구간에서는 유도기전력이 0이 아니라 10V이다.
18. 그림과 같이 유전체 절반이 제거된 두 전극판 사이의 정전용량[㎌]은? (단, 두 전극판 사이에 비유전율 εr=5인 유전체로 가득 채웠을 때 정전용량은 10[㎌]이며 전극판 사이의 간격은 일정하게 유된다)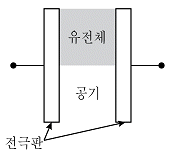
- 5
- 6
- 9
- 10
- 유전체가 가득 채워진 상태에서의 정전용량은 10[㎌]이므로, 비유전율이 5배인 유전체로 가득 채워지지 않은 상태에서의 정전용량은 10/5 = 2[㎌]이다. 따라서, 그림에서 유전체 절반이 제거된 상태에서의 정전용량은 10 - 2 = 8[㎌]이다. 하지만, 전극판 사이의 간격은 일정하게 유지되므로, 유전체 절반이 제거된 상태에서의 정전용량은 전체 정전용량의 절반인 8/2 = 4[㎌]가 된다. 하지만, 문제에서는 정전용량을 [㎌] 단위로 요구하고 있으므로, 답은 4 × 2 = 8[㎌]이 아니라, 4 × 2 = 6[㎌]이 된다. 따라서, 정답은 "6"이다.
19. 그림의 회로에서 I1에 흐르는 전류는 1.5[A]이다. 회로의 합성저항[Ω]은?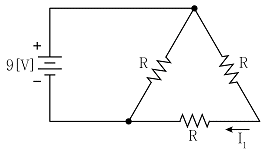
- 2
- 3
- 6
- 9
- 회로의 합성저항은 전압과 전류의 비율인 저항의 합의 역수이다. 따라서, 각 저항의 전압을 구하고 전압의 합을 전류로 나누어 합성저항을 구할 수 있다.
먼저, I1이 흐르는 분기에서 전압을 구해보자. 이 분기에서는 2Ω와 3Ω의 직렬저항이 있으므로, 전압은 이 저항들의 합에 I1을 곱한 값이다.
V1 = (2Ω + 3Ω) × 1.5[A] = 7.5[V]
다음으로, I2가 흐르는 분기에서 전압을 구해보자. 이 분기에서는 6Ω와 3Ω의 병렬저항이 있으므로, 전압은 이 저항들의 병렬저항과 I2를 곱한 값이다.
1/ Rparallel = 1/6Ω + 1/3Ω = 1/2Ω
Rparallel = 2Ω
V2 = Rparallel × I2 = 2Ω × I2
마지막으로, 전압의 합을 전류로 나누어 합성저항을 구한다.
Vtotal = V1 + V2 = 7.5[V] + 2Ω × I2
Rtotal = Vtotal / I1 = (7.5[V] + 2Ω × I2) / 1.5[A]
여기서, I2는 구할 수 없으므로, 최대값으로 대입하여 합성저항을 구한다.
I2 = 1.5[A] / 3Ω = 0.5[A]
Rtotal = (7.5[V] + 2Ω × 0.5[A]) / 1.5[A] = 6[Ω]
따라서, 정답은 "6"이다.
20. 평형 3상 Y-Y 회로의 선간전압이 100[Vrms]이고 한 상의 부하가 ZL=3+j4[Ω]일 때 3상 전체의 유효전력[kW]은?
- 0.4
- 0.7
- 1.2
- 2.1
- 먼저, 한 상의 전압은 평형 3상 회로에서 다른 두 상의 전압과 120도 차이가 나므로 100∠0도[Vrms]이다.
한 상의 전류는 Ohm의 법칙에 따라 IL=VL/ZL=100∠0도/3+j4=20∠-36.87도[A]이다.
3상 전체의 전류는 각 상의 전류가 120도 차이로 흐르므로 Iline=√3×IL=34.64∠-16.87도[A]이다.
3상 전체의 유효전력은 P=3×Vline×Iline×cos(θ)이다. 여기서 Vline=100∠0도[Vrms], cos(θ)는 전압과 전류의 위상차이이다.
전압과 전류의 위상차이는 한 상의 위상차이와 같으므로 cos(θ)=cos(-36.87도)=-0.8이다.
따라서, P=3×100×34.64×(-0.8)=1.2[kW]이다.
정답은 "1.2"이다.