1과목: 과목 구분 없음
1. KDS(2016) 설계기준에서 제시된 교량설계 원칙 중 한계상태에 대한 설명으로 옳은 것은?
- 사용한계상태는 극단적인 사용조건하에서 응력, 변형 및 균열폭을 제한하는 것으로 규정한다.
- 피로한계상태는 기대응력범위의 반복 횟수에서 발생하는 단일 피로설계트럭에 의한 응력범위를 제한하는 것으로 규정한다.
- 극한한계상태는 지진 또는 홍수 발생 시, 또는 세굴된 상황에서 선박, 차량 또는 유빙에 의한 충돌 시 등의 상황에서 교량의 붕괴를 방지하는 것으로 규정한다.
- 극단상황한계상태는 교량의 설계수명 이내에 발생할 것으로 기대되는, 통계적으로 중요하다고 규정한 하중조합에 대하여 국부적/전체적 강도와 안정성을 확보하는 것으로 규정한다.
2. 균열폭에 대한 설명으로 옳지 않은 것은?
- 균열폭을 작게 하기 위해서는 지름이 작은 철근을 많이 사용하는 것이 지름이 큰 철근을 적게 사용하는 것보다 유리하다.
- 하중에 의한 균열을 제어하기 위해 요구되는 철근 이외에도 필요에 따라 온도변화, 건조수축 등에 의한 균열을 제어하기 위해 추가적인 보강철근을 배근할 수 있다.
- 균열폭은 철근의 인장응력에 선형 또는 비선형적으로 비례한다.
- 일반적으로 피복두께가 클수록 균열폭은 작아진다.
3. KDS(2016) 설계기준에서는 휨부재의 최소 철근량으로 다음 두 가지 식으로 계산한 값 중에서 큰 값 이상을 사용한다. 이 두 가지 식을 함께 사용하는 이유는? (단, fck는 콘크리트의 설계기준 압축강도이며, fy는 철근의 설계기준 항복강도, bw는 단면의 폭, d는 단면의 유효높이이다)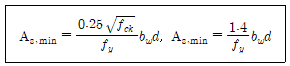
- 인장철근량을 가능한 한 줄여 휨부재의 연성파괴를 유도하기 위함이다.
- 사용 콘크리트의 압축강도가 커짐에 따라 취성이 증가하므로 이를 합리적으로 반영하기 위함이다.
- 철근의 강도가 커지면 인장철근량을 줄여 연성파괴를 유도하기 위함이다.
- 콘크리트 강도와 철근의 강도를 조절하여 가능한 한 균형단면에 가깝게 하기 위함이다.
4. 단철근 직사각형 콘크리트 보의 설계휨모멘트를 증가시키는 방법 중에서 가장 효과가 적은 것은?
- 인장철근량의 증가
- 인장철근 설계기준 항복강도의 상향
- 단면 유효깊이의 증가
- 콘크리트 설계기준 압축강도의 상향
5. 압축철근비ρ'=0.02인 복철근 직사각형 콘크리트 보에 고정하중이 작용하여 15mm의 순간처짐이 발생하였다. 1년 후 크리프와 건조수축에 의하여 보에 발생하는 추가 장기처짐[mm]은? (단, 활하중은 없으며, KDS(2016) 설계기준을 적용한다)
- 8.8
- 10.5
- 15.4
- 25.5
6. 다발철근을 사용하여 수중에서 콘크리트를 치는 경우 최소 피복두께[mm]는? (단, KDS(2016) 설계기준을 적용한다)
- 120
- 100
- 80
- 60
7. 철근의 순간격이 80mm이고 피복두께가 40mm인 보통중량콘크리트를 사용한 부재에서 D32 인장철근의 A급 겹침이음길이[mm]는? (단, 콘크리트의 설계기준 압축강도 fck=36MPa, 철근의 설계기준 항복강도 fy=400MPa, 철근은 도막되지 않은 하부에 배치되는 이형철근으로 공칭지름은 32mm이고, KDS(2016) 설계기준을 적용한다)
- 1,280
- 1,664
- 1,920
- 2,130
8. 그림과 같은 띠철근 기둥의 순수 축하중강도 P0[kN]는? (단, 기둥은 단주로서 콘크리트 설계기준 압축강도 fck=30MPa, 철근의 설계기준 항복강도 fy=400MPa, 종방향 철근 총단면적 Ast=3,000mm2이며, KDS(2016) 설계기준을 적용한다)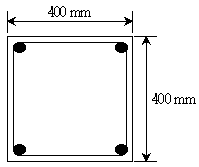
- 3,499.8
- 4,522.4
- 5,203.5
- 6,177.8
9. 그림과 같은 단면의 캔틸레버 보에 자중을 포함한 등분포 계수하중 wu=25kN/m가 작용하고 있을 때, 전단위험단면에서 전단철근이 부담해야 할 공칭전단력 Vs[kN]는? (단, 보의 지간은 3.3m, 콘크리트의 쪼갬인장강도 fsp=1.4MPa, 콘크리트의 설계기준 압축강도 fck=25MPa, 인장철근의 설계기준 항복강도 fy=350MPa이며, KDS(2016) 설계기준을 적용한다)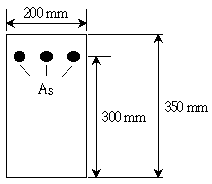
- 100
- 75
- 50
- 25
10. KDS(2016) 설계기준에서 제시된 근사해법을 적용하여 1방향 슬래브를 설계할 때 그 순서를 바르게 나열한 것은?
- ㄱ (→) ㄹ (→) ㅁ (→) ㄴ (→) ㄷ
- ㄱ (→) ㄹ (→) ㄴ (→) ㄷ (→) ㅁ
- ㄹ (→) ㅁ (→) ㄷ (→) ㄴ (→) ㄱ
- ㄹ (→) ㄱ (→) ㄴ (→) ㄷ (→) ㅁ
11. KS F 2423(콘크리트의 쪼갬인장 시험 방법)에 준하여 ø100mm×200mm 원주형 표준공시체에 대한 쪼갬인장강도 시험을 실시한 결과, 파괴 시 하중이 75kN으로 측정된 경우 쪼갬인장강도[MPa]는? (단, π=3으로 계산하며, KDS(2016) 설계기준을 적용한다)
- 1.5
- 2.0
- 2.5
- 5.0
12. 그림과 같이 연직하중 P와 휨모멘트 M이 바닥판과 기둥의 중심에 작용하는 철근콘크리트 확대기초의 최대 지반응력[kN/m2]은? (단, 기초의 자중은 무시한다)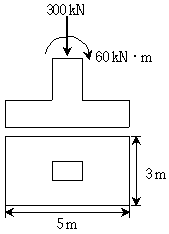
- 24.8
- 29.2
- 34.4
- 39.2
13. 12mm 두께의 강판과 10mm 두께의 강판을 필릿용접할 때 요구되는 최소 용접치수[mm]는? (단, KDS(2016) 설계기준을 적용한다)
- 12
- 10
- 6
- 4
14. 그림과 같은 중력식 옹벽의 전도에 대한 안전율은? (단, 콘크리트의 단위중량 γc=25kN/m3, 흙의 내부마찰각 ø=30°, 점착력 c=0, 흙의 단위중량 γs=20kN/m3, 옹벽 전면에 작용하는 수동토압은 무시하며, KDS(2016) 설계기준을 적용한다)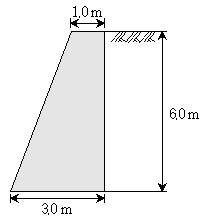
- 1.52
- 2.08
- 2.40
- 3.50
15. 그림과 같이 자중을 포함한 등분포하중 w=20kN/m가 재하된 프리스트레스트콘크리트 단순보에 긴장력 P=2,000kN이 작용할 때 보에 작용하는 순하향 하중[kN/m]은? (단, 프리스트레스의 손실은 무시한다)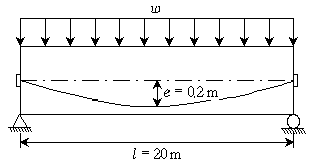
- 4
- 8
- 12
- 16
16. 길이 10m의 포스트텐셔닝 콘크리트 보의 긴장재에 1,500MPa의 프리스트레스를 도입하여 일단 정착하였더니 정착부 활동이 6mm 발생하였다. 이때 프리스트레스의 손실률[%]은? (단, 긴장재는 직선으로 배치되어 긴장재와 쉬스의 마찰은 없으며, 탄성계수 Ep=200GPa이다)
- 14
- 12
- 10
- 8
17. 그림과 같은 단철근 직사각형 콘크리트 보에 사용 가능한 최대 인장철근비 는? (단, 콘크리트의 설계기준 압축강도 fck=35MPa, 인장철근의 설계기준 항복강도 fy=255MPa, β1=0.8로 하며, KDS(2016) 설계기준을 적용한다)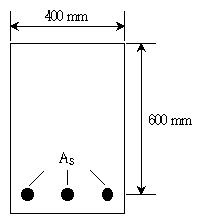
- 0.01
- 0.02
- 0.03
- 0.04
18. 500mm×500mm 정사각형 단면을 가진 비횡구속 띠철근 기둥의 장주효과를 무시할 수 있는 최대 비지지길이[m]는? (단, 기둥의 양단은 힌지로 지지되어 있으며, KDS(2016) 설계기준을 적용한다)
- 3.3
- 4.3
- 6.8
- 7.9
19. T형 프리스트레스트콘크리트 단순보에 설계하중이 작용할 때 보의 처짐은 0이었으며, 프리스트레스 도입단계부터 보의 상연에 부착된 변형률 게이지로 측정된 콘크리트 탄성변형률 εc=4.0×10-4이었다. 이 경우 초기긴장력 Pi[kN]는? (단, 콘크리트의 탄성계수 Ec=25GPa, T형보의 총단면적 Ag=170,000mm2, 프리스트레스의 유효율 R=0.85이다)
- 2,000
- 1,800
- 1,600
- 1,400
20. KDS(2016) 설계기준에서 제시된 교량 내진설계에 관한 내용 중에서 옳지 않은 것은?
- 위험도계수 I는 평균재현주기가 1,000년인 지진의 유효수평지반가속도 S를 기준으로 평균재현주기가 다른 지진의 유효수평지반가속도의 상대적 비율을 의미한다.
- 교량의 지진하중을 결정하는데 사용되는 지반계수는 지반상태가 탄성지진응답계수에 미치는 영향을 반영하기 위한 보정계수이다.
- 교량의 내진등급은 중요도에 따라 내진특등급, 내진I등급, 내진II등급으로 분류하며 지방도의 교량은 내진I등급이다.
- 교량이 위치할 부지에 대한 지진지반운동의 유효수평지반가속도 S는 지진구역계수 Z에 각 평균재현주기의 위험도계수 I를 곱하여 결정한다.





