1과목: 과목 구분 없음
1. 그림과 같이 높이(h)가 800mm이고, 길이(L)가 20m인 PSC 단순보에서, 긴장력(P) 8,000kN을 작용시켰을 때, 긴장력에 의한 등가등분포 상향력 U[kN/m]는? (단, 중앙부 편심(e) 300mm, 양 단부 편심(e) 0mm로 2차 포물선으로 긴장재가 배치되어 있으며, 자중 및 긴장력 손실은 무시한다)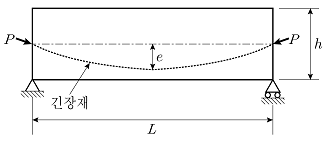
- 48
- 34
- 20
- 16
2. 그림과 같이 기둥의 단부 조건이 양단 힌지이며, 비지지길이가 ℓu인 기둥의 좌굴하중은? (단, E는 탄성계수, I는 단면2차모멘트이며, 탄성 좌굴로 거동한다.)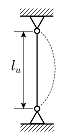
3. 그림과 같은 복철근 직사각형보의 공칭휨강도 Mn및 등가직사각형 응력블록의 깊이 a를 구하는 식은? (단, 인장철근 및 압축철근은 항복하였고, 콘크리트 설계기준압축강도는 fck, 철근의 설계기준항복강도는 fy이며, 콘크리트구조 휨 및 압축 설계기준(KDS 14 20 20: 2016)을 따른다) (순서대로 Mn, a)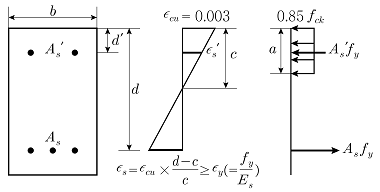
4. 포스트텐션에 의한 프리스트레스를 도입할 때 발생 가능한 즉시 손실의 원인만을 모두 고르면?
- ㄱ, ㄴ, ㅁ
- ㄱ, ㄷ, ㅂ
- ㄴ, ㄷ, ㄹ
- ㄴ, ㄷ, ㅂ
5. 편심이 없는 중심 축하중만을 받는 I형 단면을 가진 강재 기둥 설계에 대한 설명으로 옳지 않은 것은? (단, 자중 및 국부좌굴은 고려하지 않는다)
- 하중이 임계좌굴하중에 도달하면 기둥은 세장비가 가장 작은 주축에 대해 좌굴이 발생한다.
- 지점조건, 비지지길이, 단면적이 모두 일정할 때 단면의 회전반경이 증가하면 좌굴하중은 증가한다.
- 탄성좌굴을 유발하는 평균압축응력은 세장비의 제곱에 반비례한다.
- 좌굴응력이 비례한계보다 작은 경우, 탄성상태에서 좌굴이 발생한다.
6. 그림과 같이 슬래브와 보를 일체로 타설한 경간이 20m인 단순지지된 철근콘크리트 보가 있다. 빗금친 T형 단면에 대한 내용으로 옳은 것은? (단, 콘크리트구조 해석과 설계 원칙(KDS 14 20 10: 2016)을 따른다)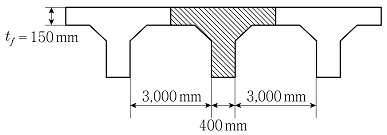
- tf를 180mm로 증가시키면 빗금친 T형 단면의 유효폭(b)은 증가한다.
- 경간 중앙의 T형 단면에서 종방향 휨모멘트에 의해 슬래브 콘크리트 전체 단면이 종방향 인장응력을 받는다.
- 등가직사각형 응력블록 깊이(a)가 tf보다 크면 직사각형 단면으로 간주하여 해석한다.
- 빗금친 T형 단면의 유효폭(b)은 3,000mm이다.
7. 단면이 두꺼운 매스콘크리트 교량 확대기초 시공 시 온도균열의 방지나 제어를 위해 고려하는 방안으로 적절하지 않은 것은?
- 프리쿨링 또는 파이프쿨링을 적절히 적용한다.
- 1종 시멘트를 조강 시멘트로 대체하여 사용한다.
- 1회당 콘크리트 타설 높이를 적절하게 나누어 시공한다.
- 1종 시멘트 대신 중용열 시멘트 또는 저발열 시멘트를 사용한다.
8. 암거와 라멘 구조물의 설계에 대한 설명으로 옳은 것은?
- 토압이 작용하는 경우 측벽에 작용하는 토압은 깊이에 따라 일정한 직사각형 분포로 고려한다.
- 상자암거 설계에서 활하중을 고려하지 않는다.
- 매설된 경우에 매설깊이는 고려할 필요가 없다.
- 라멘 구조물의 경우 일반적으로 수평부재와 연직부재가 만나는 절점부에서 모멘트에 대한 수평부재의 위험단면은 연직부재의 전면으로 볼 수 있다.
9. 휨모멘트와 축력을 받는 철근콘크리트 부재의 설계를 위한 일반 가정으로 옳지 않은 것은? (단, 콘크리트구조 휨 및 압축 설계기준(KDS 14 20 20: 2016)을 따른다)
- 인장철근이 설계기준항복강도 fy에 대응하는 변형률에 도달하고 동시에 압축연단 콘크리트가 가정된 극한변형률인 0.003에 도달할 때, 그 단면이 균형변형률 상태에 있다고 본다.
- 압축연단 콘크리트가 가정된 극한변형률인 0.003에 도달할 때 최외단 인장철근의 순인장변형률 εt가 압축지배변형률 한계 이하인 단면을 압축지배단면이라고 한다.
- 휨부재의 강도를 증가시키기 위하여 추가 인장철근과 이에 대응하는 압축철근을 사용할 수 있다.
- 압축연단 콘크리트가 가정된 극한변형률인 0.003에 도달할 때 최외단 인장철근의 순인장변형률 εt가 0.003인 단면은 인장지배단면으로 분류된다.
10. 그림과 같은 단면을 가진 T형보에 정모멘트가 작용할 때 극한상태에서의 등가직사각형 응력블록의 깊이 a가 200mm라면 콘크리트에 작용하는 압축력의 크기[kN]는? (단, fck=24MPa, fy=400MPa이며, 콘크리트구조 휨 및 압축 설계기준(KDS 14 20 20: 2016)을 따른다)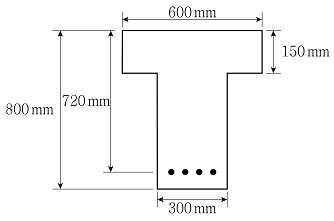
- 2,142
- 2,448
- 2,520
- 2,880
11. 전단철근이 부담해야 할 전단력 Vs=500kN일 때, 전단철근(수직스터럽)의 간격 s를 240mm로 하면 직사각형 단면에서 필요한 최소 유효깊이 d[mm]는? (단, 보통중량콘크리트이며 fck=36MPa, fy=400MPa, b=400mm, 전단철근의 면적 Av=500mm2이고, 콘크리트구조 전단 및 비틀림 설계기준(KDS 14 20 22: 2016)을 따른다. 또한, 전단철근 최대간격 기준을 만족한다.)
- 550
- 600
- 650
- 700
12. 그림과 같이 기초에 편심하중이 작용할 때 기초 저면에 생기는 응력 분포 형상은? (단, 단위폭으로 고려하고, e=100mm, 지반 조건은 균일하며, 자중은 무시한다)
13. 그림과 같이 중립축으로부터 편심거리 e만큼 떨어진 지점에 긴장력 P를 작용시킨 프리스트레스트 콘크리트(PSC) 보의 중앙 단면에서의 응력 분포로 적절한 것은? (단, PSC 보의 프리스트레스만을 고려하고 자중은 무시하며, (+)는 압축응력, (-)는 인장응력으로 정의한다. 단면은 직사각형이며, 이외 다른 조건은 고려하지 않는다)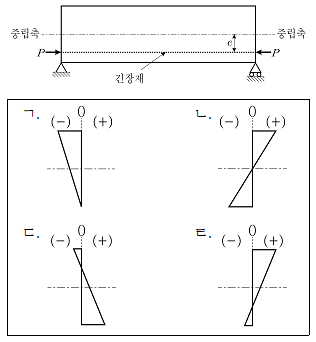
- ㄱ
- ㄴ
- ㄷ
- ㄹ
14. 그림과 같이 1방향 슬래브 단면에 주철근으로 D13 철근을 200mm 간격으로 보강하여 휨설계를 하고자 할 때, 등가직사각형 응력블록의 깊이 a[mm]는? (단, D13 철근 하나의 공칭단면적은 126mm2로 하고, 유효깊이 d=170mm, fck=21MPa, fy=340MPa이며, 콘크리트구조 휨 및 압축 설계기준(KDS 14 20 20: 2016)을 따른다)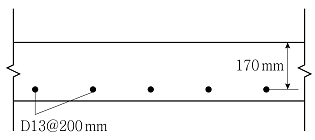
- 9.0
- 10.5
- 12.0
- 12.6
15. 철근콘크리트 구조물에서 부착 철근의 중심 간격이 5(cc+db/2)이하인 경우, 설계 균열폭을 감소시킬 수 있는 방법으로 옳지 않은 것은? (단, cc는 최외단 인장철근의 최소피복두께, db는 철근 공칭지름을 의미하며, 콘크리트구조 사용성 설계기준(KDS 14 20 30: 2016)을 따른다)
- 원형철근 대신 이형철근을 사용한다.
- 철근의 순피복 두께를 크게 한다.
- 동일한 철근비에 대해 지름이 작은 철근을 사용한다.
- 동일한 철근 지름에 대해 철근비를 크게 한다.
16. 휨부재에서 fck=25MPa, fy=500MPa일 때 인장 이형철근(D25)의 겹침이음 길이[mm]는? (단, 콘크리트구조 정착 및 이음 설계기준(KDS 14 20 52: 2016)을 따르며, λ=1.0, db=25mm, 배근 철근량/소요 철근량=1.5로 한다)
- 1,500
- 1,650
- 1,800
- 1,950
17. 폭이 400mm, 높이가 400mm인 철근콘크리트 보에 대해 비틀림의 영향을 무시할 수 없는 계수 비틀림모멘트의 최솟값[kNㆍm]은? (단, fck=36MPa인 보통중량콘크리트 보이며, 콘크리트구조 전단 및 비틀림 설계기준(KDS 14 20 22: 2016)을 따르고, 비틀림모멘트만을 고려한다)
- 4
- 6
- 8
- 10
18. 그림은 철근콘크리트 단순보에서 철근 배근을 표현한 것이다. 자중의 영향만을 고려할 때 전단철근과 지간 중앙에서의 압축철근을 바르게 연결한 것은? (단, 왼쪽 하단에 지점으로 지지되어 있다) (순서대로 전단철근, 압축철근)
- ㉠:㉡, ㉢
- ㉠:㉡, ㉣
- ㉡:㉣, ㉠
- ㉡:㉣, ㉢
19. 그림과 같은 동일 재질의 강재로 만들㎣어진 직사각형 단면에 대해 x-x축에 대한 소성단면계수[×106]는? (단, 좌굴은 고려하지 않는다)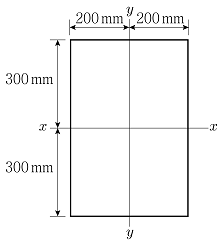
- 6
- 12
- 24
- 36
20. 토목 철근콘크리트 구조물의 설계 방법에 대한 설명으로 옳지 않은 것은?
- 허용응력설계법은 구조물을 안전하게 설계하기 위해 하중에 의해 부재에 유발된 응력이 허용응력을 초과하였는지를 검증한다.
- 한계상태설계법은 하중과 재료에 대하여 각각 하중계수와 재료계수를 사용하여 이들의 특성을 설계에 합리적으로 반영한다.
- 설계법은 이론, 재료, 설계 및 시공 기술 등의 발전과 더불어 강도설계법→허용응력설계법→한계상태설계법 순서로 발전되었다.
- 강도설계법은 기본적으로 부재의 파괴상태 또는 파괴에 가까운 상태에 기초를 둔 설계법이다.






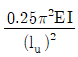
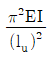
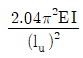
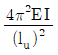
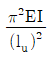 " 이다.
" 이다.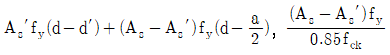
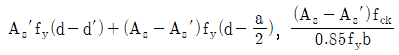

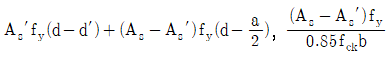
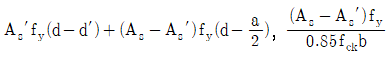 "이다. 이유는 등가직사각형 응력블록의 깊이 a는 인장존의 균일한 응력을 가지는 최대 깊이인 xu에 의존하며, xu는 fck/fy의 값이 커질수록 작아지기 때문이다. 따라서, fck/fy의 값이 커질수록 등가직사각형 응력블록의 깊이 a는 작아지게 된다.
"이다. 이유는 등가직사각형 응력블록의 깊이 a는 인장존의 균일한 응력을 가지는 최대 깊이인 xu에 의존하며, xu는 fck/fy의 값이 커질수록 작아지기 때문이다. 따라서, fck/fy의 값이 커질수록 등가직사각형 응력블록의 깊이 a는 작아지게 된다.



 "이다. 이유는 편심하중이 작용하는 위치가 중심에서 멀어질수록 응력이 증가하는 것을 고려할 때, 기초 저면의 왼쪽 부분에서는 응력이 증가하다가 오른쪽 부분에서는 감소하기 때문이다. 따라서, 기초 저면의 중심에서 멀어질수록 응력이 증가하다가 다시 감소하는 형상을 가지는 "
"이다. 이유는 편심하중이 작용하는 위치가 중심에서 멀어질수록 응력이 증가하는 것을 고려할 때, 기초 저면의 왼쪽 부분에서는 응력이 증가하다가 오른쪽 부분에서는 감소하기 때문이다. 따라서, 기초 저면의 중심에서 멀어질수록 응력이 증가하다가 다시 감소하는 형상을 가지는 "
U = P/(2L) * (h^2/4 - e^2)
여기서 P는 주어진 긴장력 8,000kN, L은 20m, h는 800mm(0.8m), e는 중앙부 편심 300mm(0.3m)이므로,
U = 8,000/(2*20) * (0.8^2/4 - 0.3^2) = 48 (kN/m)
따라서 정답은 "48"이다.