1과목: 과목구분없음
1. 그림과 같이 건물 옥상에서 물체를 가만히 놓았더니 연직 아래로 떨어졌다. 그래프는 이 물체의 속도를 시간에 따라 나타낸 것이다. 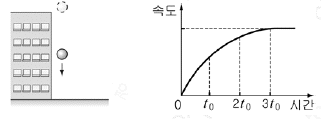
이 물체의 운동에 대한 옳은 설명을 <보기>에서 모두 고른 것은?
- ㄱ
- ㄷ
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
2. 그림과 같이 자동차가 A지점에서 출발하여 B지점까지 등가속도 직선 운동을 하였고, B지점에서부터는 일정한 속력으로 원운동하였다. A에서 B까지의 거리 100m를 이동하는 데 걸린 시간은 10초이다. 
이 자동차의 운동에 대한 옳은 설명을 <보기>에서 모두 고른 것은? (단, 자동차의 크기는 무시한다.)
- ㄱ
- ㄴ
- ㄷ
- ㄱ, ㄴ
- ㄴ, ㄷ
3. 다음은 시간기록계를 이용하여 중력가속도를 측정하는 실험 과정이다. 
이에 대해 옳게 말한 사람을 <보기>에서 모두 고른 것은?
- 철수
- 영희
- 철수, 민수
- 영희, 민수
- 철수, 영희, 민수
4. 그래프는 수평면으로부터 높이 h인 지점에서 질량이 0.2kg인 물체를 가만히 놓았을 때 운동하는 물체의 속도를 시간에 따라 나타낸 것이다. 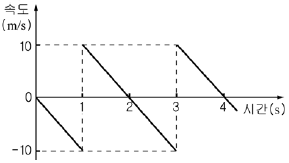
이에 대한 옳은 설명을 <보기>에서 모두 고른 것은? (단, 공기 저항과 물체의 크기는 무시한다.) [3점]
- ㄴ
- ㄷ
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄱ, ㄴ, ㄷ
5. 그림과 같이 15m 떨어진 곳에서 질량이 같은 물체 A, B를 동시에 수평방향으로 각각 20m/s, 10m/s의 속력으로 던졌더니, 두 물체가 충돌하여 한 덩어리가 되었다. 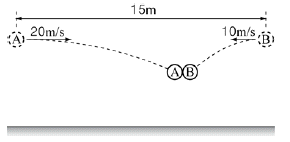
충돌 직후 한 덩어리가 된 물체의 속력은? (단, 중력가속도는 10 m/s2 고, 공기 저항과 물체의 크기는 무시한다.) [3점]
- 5m/s
- 5√2m/s
- 10m/s
- 10√2m/s
- 20m/s
6. 그림과 같이 수평면으로부터 높이 H인 경사면 위에 물체 A를 가만히 놓았더니, 수평면에 정지해 있던 물체 B와 정면충돌하였다. 충돌 후 A는 정지하였고, B는 수평면을 따라 운동하다 경사면을 올라갔다. A, B의 질량은 각각 m, 2m이다. 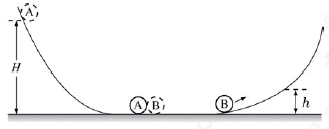
충돌 후 수평면으로부터 B가 올라간 최고 높이 h는? (단, 공기 저항, 모든 마찰과 물체의 크기는 무시한다.) [3점]
- 1/5 H
- 1/4 H
- 1/3 H
- 1/2 H
- 2/3 H
7. 그림과 같이 천장에 연결된 실에 매달려 있는 물체를 점 P에 가만히 놓았더니 물체가 최저점 Q와 점 R를 차례대로 지나 운동 하였다. 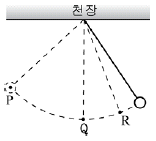
이 물체의 운동과 힘에 대한 옳은 설명을 <보기>에서 모두 고른 것은? (단, 공기 저항과 물체의 크기는 무시한다.)
- ㄴ
- ㄷ
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄱ, ㄴ, ㄷ
8. 그림은 마찰이 없는 수평면에서 질량이 같은 물체 A, B, C가 일직선 상에서 오른쪽으로 운동하는 것을 나타낸 것이고, A의 속도는 v로 일정하다. 그래프는 A에 대한 B(실선), A에 대한 C(점선)의 속도를 시간에 따라 나타낸 것이다. B와 C는 t초일 때 정면충돌한다. 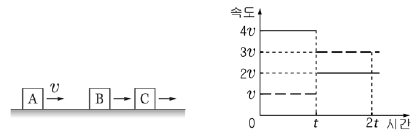
B와 C 사이의 반발계수는? (단, 공기 저항과 물체의 크기는 무시한다.)
- 1/5
- 1/3
- 1/2
- 3/4
- 4/5
9. 그림은 xy 수평면에서 물체 A가 -y방향으로 등속 직선 운동하고 물체 B는 +x방향으로 등가속도 직선 운동하는 것을, 그래프는 A, B의 속력을 시간에 따라 나타낸 것이다. 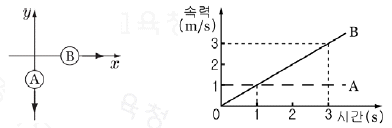
A, B의 운동에 대한 옳은 설명을 <보기>에서 모두 고른 것은? [3점]
- ㄱ
- ㄴ
- ㄷ
- ㄱ, ㄴ
- ㄴ, ㄷ
10. 그림과 같이 지면으로부터 높이 H 인 지점에서 수평하게 던져진 물체 A가 점 p를 지나는 순간 점 q에서 물체 B를 가만히 놓았더니, A와 B가 동시에 지면에 도달하였다. 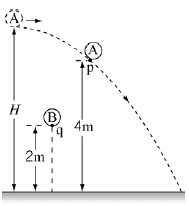
H는? (단, 공기 저항과 물체의 크기는 무시한다.) [3점]
- 4.5m
- 4.7m
- 5.0m
- 5.2m
- 5.5m
11. 수평면이 물체를 떠받치는 힘의 크기는?(11번 공통지문 문제)
12. 그림 (가), (나)는 정지위성 A, B가 지구 주위를 등속 원운동하는 모습을 나타낸 것이다. 정지위성의 공전 주기는 지구의 자전 주기와 같다. 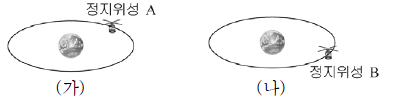
A의 질량이 B의 질량의 2배일 때, 두 정지위성의 운동에 대한 옳은 설명을 <보기>에서 모두 고른 것은? [3점]
- ㄱ
- ㄴ
- ㄷ
- ㄱ, ㄷ
- ㄴ, ㄷ
13. 그림은 질량이 같은 물체 A, B가 행성을 중심으로 등속 원운동하고 있는 것을 나타낸 것이다. A, B의 궤도 반지름은 각각 r0, 2r0이다. 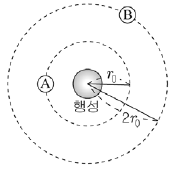
A, B의 속력을 각각 vA, vB라 할 때, vA : vB는? (단, 물체에는 행성에 의한 만유인력만 작용한다.)
- 1 : 1
- 1 : √2
- 1 : 4
- √2 : 1
- 2 : 1
14. 그림과 같이 영희가 속력 v0으로 물체 A를 연직 위 방향으로 던진 순간부터 T초 후 다시 같은 속력 v0으로 물체 B를 던졌더니, B를 던진 순간부터 t초 후 A와 B가 만났다. A와 B가 영희의 손을 떠난 높이는 같다. 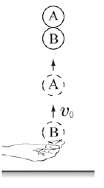
t는? (단, 중력가속도는 g이고, 공기 저항과 물체의 크기는 무시한다.) [3점]
15. 그림 (가), (나)와 같이 용수철상수가 같은 용수철에 연결된 물체를 각각 L, 2L만큼 당겼다가 놓았더니 단진동하였다. 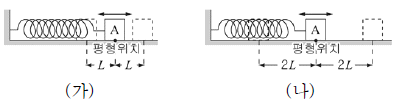
A의 운동과 에너지에 대한 옳은 설명을 <보기>에서 모두 고른 것은?
- ㄱ
- ㄴ
- ㄷ
- ㄱ, ㄴ
- ㄴ, ㄷ
16. 그림과 같이 마찰이 없는 xy 수평면에서 물체 A는 x축과 30°를 이루는 방향으로 일정한 속력 v0으로 운동하고, 물체 B는 -y 방향으로 일정한 속력v0으로 운동한다. A, B는 O점에서 충돌한 후 한 덩어리가 되어 +x 방향으로 운동한다. A, B의 질량은 각각 2m, m이다. 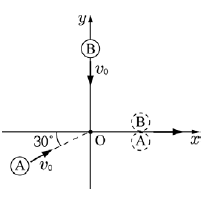
충돌 과정에서 B가 A로부터 받은 충격량의 크기는? (단, 공기저항과 물체의 크기는 무시한다.) [3점]
17. 그림은 수평면에서 용수철에 연결된 물체가 단진동하는 모습을, 그래프는 이 물체의 운동에너지를 시간에 따라 나타낸 것이다. 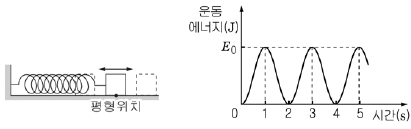
이 물체의 운동과 에너지에 대한 옳은 설명을 <보기>에서 모두 고른 것은? (단, 용수철의 질량은 무시한다.) [3점]
- ㄱ
- ㄴ
- ㄱ, ㄴ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
18. 그림은 일정한 주기로 회전하고 있는 풍력 발전기의 모습을 나타낸 것이다. 
점 A, B, C의 구심 가속도를 각각 aA, aB, aC라 할 때 aA, aB, aC의 크기를 바르게 비교한 것은?
- aA > aB > aC
- aA > aB = aC
- aA = aB = aC
- aA = aB < aC
- aA < aB < aC
19. 그림과 같이 물체 A는 행성의 중심으로부터 반지름이 2r0인 궤도를 등속 원운동하고, 물체 B는 행성에 가까워지는 방향으로 직선 운동한다. A, B의 질량은 각각 2m, 3m이고, 역학적 에너지는 서로 같다. 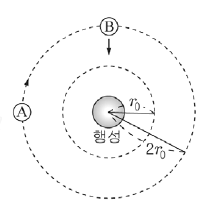
A의 운동에너지가 E0일 때, 행성의 중심으로부터 거리가 r0인 곳에서 B의 운동에너지는? (단, 물체에는 행성에 의한 만유인력만 작용한다.)
- 2E0
- 3E0
- 5E0
- 6E0
- 8E0






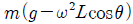
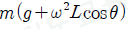
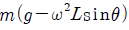
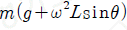
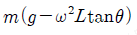
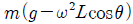 " 이다. 다른 보기들은 물체의 운동 상태와 관련된 힘들이므로, 수평면이 물체를 떠받치는 힘과는 관련이 없다.
" 이다. 다른 보기들은 물체의 운동 상태와 관련된 힘들이므로, 수평면이 물체를 떠받치는 힘과는 관련이 없다.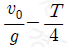
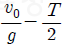
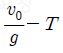
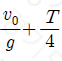
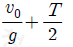
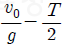 " 이다.
" 이다.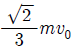
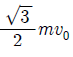
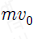
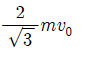
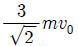
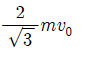 " 이다.
" 이다.