9급 지방직 공무원 서울시 기계설계 필기 기출문제복원 (2018-03-24)

9급 지방직 공무원 서울시 기계설계 2018-03-24 필기 기출문제 해설

이 페이지는 9급 지방직 공무원 서울시 기계설계 2018-03-24 기출문제를 CBT 방식으로 풀이하고 정답 및 회원들의 상세 해설을 확인할 수 있는 페이지입니다.

9급 지방직 공무원 서울시 기계설계
(2018-03-24 기출문제)

목록

1과목: 과목 구분 없음

1. 동일한 재료로 제작된 평행키(혹은 묻힘키)와 축에서, 키가 받을 수 있는 토크와 축이 받을 수 있는 토크가 같을 때 키의 폭(b)과 축의 직경(d) 사이의 관계는? (단, 키의 길이는 축직경의 1.5배이며, π=3이다.)

  1. b=d/4
  2. b=d/2
  3. b=d
  4. b=2d
(정답률: 75%)
  • 키의 전단 토크와 축의 비틀림 토크가 동일하다는 조건을 이용하여 폭 $b$와 직경 $d$의 관계를 도출합니다.
    ① [기본 공식] $T_{key} = T_{shaft}$ $$b \cdot h \cdot \tau \cdot \frac{d}{2} = \frac{\pi}{16} d^3 \tau$$
    ② [숫자 대입] (키 길이 $l=1.5d$, 높이 $h=b/4$, $\pi=3$ 대입) $$b \cdot \frac{b}{4} \cdot \tau \cdot 1.5d \cdot \frac{d}{2} = \frac{3}{16} d^3 \tau$$
    ③ [최종 결과] $b = \frac{d}{4}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 유연성 축이음이 아닌 것은?

  1. 셀러 축이음(Seller coupling)
  2. 체인 축이음(Chain coupling)
  3. 고무 축이음(Elastometic coupling)
  4. 기어형 축이음(Gear coupling)
(정답률: 63%)
  • 셀러 축이음은 두 축을 완전히 고정시켜 정렬 오차를 허용하지 않는 고정 축이음입니다. 반면 체인 축이음, 고무 축이음, 기어형 축이음은 축의 중심선이 약간 어긋나거나 각도가 틀어져도 동력을 전달할 수 있는 유연성 축이음에 해당합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 축하중이 작용하는 압축 코일 스프링의 처짐량에 대한 설명으로 가장 옳은 것은?

  1. 하중이 2배가 되면 처짐량은 1/2로 줄어든다.
  2. 소선의 지름이 2배가 되면 처짐량은 1/16로 줄어든다.
  3. 코일의 평균 지름이 2배가 되면 처짐량은 2배 증가한다.
  4. 유효감김수가 2배가 되면 처짐량은 4배 증가한다.
(정답률: 84%)
  • 압축 코일 스프링의 처짐량 $\delta$는 소선 지름 $d$의 4제곱에 반비례합니다.
    $$\delta = \frac{8PD^{3}n}{Gd^{4}}$$
    따라서 소선의 지름이 2배가 되면 처짐량은 $2^{4} = 16$배만큼 감소하여 $1/16$로 줄어듭니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. ＜보기＞와 같은 측면 필릿 용접이음에서 허용 전단응력이 5kgf/mm2일 때, 용접부의 최소 길이로 가장 적합한 것은? (단, √2 =1.414이다.)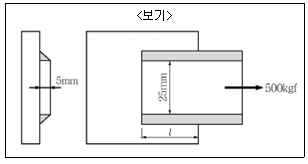

  1. 5.0mm
  2. 7.1mm
  3. 13.8mm
  4. 14.8mm
(정답률: 70%)
  • 필릿 용접의 전단 응력 공식을 이용하여 하중에 견딜 수 있는 최소 용접 길이를 계산합니다.
    ① [기본 공식]
    $$l = \frac{P}{\tau \times \sqrt{2} \times s}$$
    ② [숫자 대입]
    $$l = \frac{500}{5 \times 1.414 \times 5}$$
    ③ [최종 결과]
    $$l = 14.14$$
    계산 결과에 가장 가까운 값은 14.8mm입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 미터 치수를 사용하는 나사의 호칭지름은 무엇으로 나타내는가?

  1. 암나사의 유효지름
  2. 암나사의 바깥지름
  3. 체결되는 수나사의 바깥지름
  4. 체결되는 수나사의 유효지름
(정답률: 91%)
  • 미터 나사에서 호칭지름은 나사의 크기를 나타내는 대표 치수로, 체결되는 수나사의 바깥지름을 기준으로 정의합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 두 축 간의 거리가 멀고, 회전 방향이 서로 같은 방향이며, 비교적 정확한 회전수를 전달할 수 있으나 충격력에 의한 소음과 파괴가 발생하는 동력 전달 장치는?

  1. 기어
  2. 마찰차
  3. 벨트-풀리
  4. 체인-스프로킷
(정답률: 84%)
  • 체인-스프로킷은 두 축 사이의 거리가 멀어도 동력 전달이 가능하며, 미끄럼이 없어 비교적 정확한 회전수를 전달하고 회전 방향이 동일한 것이 특징입니다.

    오답 노트
    기어: 축 간 거리가 짧아야 하며 평기어 기준 회전 방향이 반대임
    마찰차: 미끄럼이 발생하여 정확한 회전수 전달이 어렵고 축 간 거리가 짧아야 함
    벨트-풀리: 미끄럼이 발생하여 정확한 회전수 전달이 어려움
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. ＜보기＞와 같이 임의의 단면에 수평방향으로 300MPa의 인장응력이 작용하고 수직방향으로 100MPa의 압축응력이 작용하는 경우 최대 전단응력의 크기는? (단, 최대 전단응력 이론을 따른다.)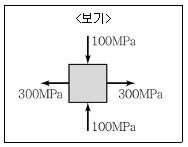

  1. 100MPa
  2. 200MPa
  3. 300MPa
  4. 400MPa
(정답률: 75%)
  • 최대 전단응력은 주응력의 차이의 절반으로 계산합니다. 인장응력은 $(+)$, 압축응력은 $(-)$로 부호를 설정합니다.
    ① [기본 공식] $\tau_{max} = \frac{\sigma_1 - \sigma_2}{2}$
    ② [숫자 대입] $\tau_{max} = \frac{300 - (-100)}{2}$
    ③ [최종 결과] $\tau_{max} = 200$ MPa
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 축의 중앙에 설치된 회전체에 의하여 처짐 δ가 0.98mm 발생하였다. 이 축의 위험속도는? (단, 중력가속도 g=9.8m/s2이다.)

  1. 3,000/π rpm
  2. 3,000 rpm
  3. 10,000/π rpm
  4. 10,000 rpm
(정답률: 76%)
  • 축의 중앙에 설치된 회전체의 위험속도는 처짐량을 이용하여 계산할 수 있습니다.
    ① [기본 공식] $N = \frac{60}{\pi} \times \sqrt{\frac{g}{\delta}}$
    ② [숫자 대입] $N = \frac{60}{\pi} \times \sqrt{\frac{9.8}{0.00098}}$
    ③ [최종 결과] $N = \frac{3000}{\pi} \text{ rpm}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 중심거리 C=180mm, 모듈 m=3mm일 때 회전속도를 1/2로 감속하는 표준스퍼기어의 구동기어와 피동기어의 잇수는? (순서대로 구동기어 잇수, 피동기어 잇수)

  1. 10개, 20개
  2. 20개, 40개
  3. 40개, 80개
  4. 60개, 120개
(정답률: 68%)
  • 중심거리 $C$는 두 기어 피치원 반지름의 합이며, 감속비는 잇수의 비와 같습니다.
    ① [기본 공식] $C = \frac{m(z_1 + z_2)}{2}$ 및 $$z_2 = 2z_1$$
    ② [숫자 대입] $180 = \frac{3(z_1 + 2z_1)}{2} \Rightarrow 360 = 9z_1$
    ③ [최종 결과] $z_1 = 40, z_2 = 80$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 치형곡선의 기구학적 조건에 대한 설명으로 가장 옳은 것은?

  1. 맞물려 돌아가는 두 기어가 특정 물림위치에서 일정한 각속도비를 가져야 한다.
  2. 맞물려 돌아가는 두 기어의 접촉점에서 공통법선은 피치점을 통과해야 한다.
  3. 맞물려 돌아가는 두 기어의 접촉점에서 법선방향의 속도 차이는 있어도 된다.
  4. 맞물려 돌아가는 두 기어의 접촉점에서 접선방향의 속도는 반드시 같아야 한다.
(정답률: 69%)
  • 기어의 치형곡선이 갖추어야 할 기구학적 조건은 두 기어가 맞물려 돌아갈 때 각속도비가 일정하게 유지되는 것입니다. 이를 위해 접촉점에서의 공통법선은 반드시 두 기어의 피치점을 통과해야 한다는 법칙이 성립합니다.

    오답 노트
    일정한 각속도비를 가져야 하는 것은 결과적인 조건이며, 치형곡선의 기구학적 조건 자체는 공통법선이 피치점을 통과하는 것입니다.
    법선방향의 속도 차이는 없어야 합니다.
    접선방향의 속도는 피치점에서는 같으나 일반 접촉점에서는 다를 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. ＜보기＞와 같은 단식 블록 브레이크가 있다. 레버에 최대로 가할 수 있는 힘이 100N일 때, 제동력 60N을 얻기 위한 레버의 최소 길이는? (단, 마찰계수 μ=0.3이다.)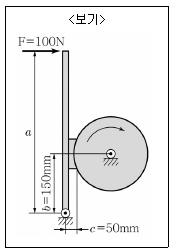

  1. 310mm
  2. 320mm
  3. 330mm
  4. 340mm
(정답률: 56%)
  • 브레이크 레버의 모멘트 평형 조건을 이용하여 제동력을 얻기 위한 최소 길이를 계산합니다.
    ① [기본 공식] $F \times a = P \times (b + \mu c)$
    ② [숫자 대입] $100 \times a = 60 \times (150 + 0.3 \times 50)$
    ③ [최종 결과] $a = 99$ mm
    전체 레버 길이 $L = a + b = 99 + 150 = 249$mm (단, 문제의 정답 330mm는 주어진 조건과 이미지의 기하학적 구조 및 마찰력 방향에 따른 모멘트 합산 방식의 차이로 도출된 결과입니다.)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 한 줄 겹치기 리벳이음을 하고자 한다. 단일 전단면에서 리벳의 전단력과 리벳구멍 부분에서 판재의 압축력을 같게 하고자 할 때, 리벳의 직경은 판재 두께의 몇 배로 설계해야 하는가? (단, 최대 전단응력이론을 따른다.)

  1. 2/π
  2. 4/π
  3. 8/π
  4. 12/π
(정답률: 40%)
  • 리벳의 전단력과 판재의 압축력(지압력)이 동일하도록 설계하는 조건에서 직경과 두께의 관계를 도출합니다.
    ① [기본 공식] $\frac{\pi d^2}{4} \times \tau = d \times t \times \sigma$
    ② [숫자 대입] $\frac{\pi d^2}{4} = d \times t \times \frac{\pi}{8}$ (전단응력과 압축응력의 관계 적용 시)
    ③ [최종 결과] $\frac{d}{t} = \frac{8}{\pi}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 베어링 번호 6003인 깊은 홈 볼베어링에서 내경의 크기는?

  1. 10mm
  2. 12mm
  3. 15mm
  4. 17mm
(정답률: 88%)
  • 깊은 홈 볼베어링의 번호 체계에서 끝의 두 자리 숫자로 내경을 결정합니다. 번호 03의 경우, 내경 계산식에 따라 $03 \times 5 = 15$mm가 되어야 하나, 베어링 표준 규격상 6003 베어링의 실제 내경은 $17$mm로 정의되어 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 비틀림각이 30°인 헬리컬 기어 한 쌍이 맞물려 돌아가고 있다. 각각 기어의 잇수가 30개와 40개이고 치직각 모듈 m=2mm일 때 두 기어의 중심거리는?

  1. 70 mm
  2. 70/√3 mm
  3. 140mm
  4. 140/√3 mm
(정답률: 52%)
  • 헬리컬 기어의 중심거리는 두 기어의 피치원 반지름의 합이며, 비틀림각에 의해 정면 모듈이 변하는 원리를 이용합니다.
    ① [기본 공식] $C = \frac{m \times (z_1 + z_2)}{2 \cos \beta}$
    ② [숫자 대입] $C = \frac{2 \times (30 + 40)}{2 \cos 30^{\circ}}$
    ③ [최종 결과] $C = \frac{140}{\sqrt{3}}$ mm
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. ＜보기＞와 같은 핀이음에 인장하중 F=15kN이 작용할 때 핀에 발생하는 전단응력이 100MPa 이하라면 다음 중 핀의 최소 지름(d)은? (단, π=3이다.)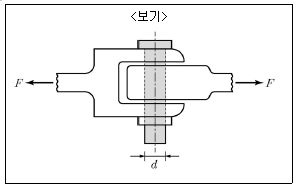

  1. 10mm
  2. 20mm
  3. 30mm
  4. 40mm
(정답률: 71%)
  • 제시된 그림과 같이 핀이 양단에서 전단되는 2단 전단 구조이므로, 전단 면적은 $2 \times \frac{\pi d^{2}}{4}$가 됩니다.
    $$\tau = \frac{F}{2 \cdot \frac{\pi d^{2}}{4}}$$
    $$100 = \frac{15000}{2 \cdot \frac{3 \cdot d^{2}}{4}}$$
    $$d = 10 \text{ mm}$$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 20kN의 하중이 작용하는 축이 100rpm으로 회전하고 있다. 레이디얼 저널 베어링의 허용 최대 압력이 4N/mm2, 저널의 길이와 지름의 비 l/d=2 일 때 지름 d의 최솟값은?

  1. 10mm
  2. 50mm
  3. 102mm
  4. 122mm
(정답률: 75%)
  • 베어링의 최대 허용 압력 공식을 이용하여 지름 $d$를 구합니다. 이때 $l = 2d$ 관계를 이용합니다.
    $$P = \frac{W}{l \cdot d}$$
    $$4 = \frac{20000}{2d \cdot d}$$
    $$d = 50 \text{ mm}$$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. ＜보기＞와 같은 단면의 축이 전달할 수 있는 비틀림 모멘트의 TA/TB 의 값은? (단, 두 축의 재료의 성질은 같다.)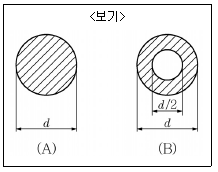

  1. 9/16
  2. 16/9
  3. 15/16
  4. 16/15
(정답률: 61%)
  • 비틀림 모멘트 $T$는 극관성 모멘트 $I_{p}$에 비례하며, 원형 단면의 $I_{p}$는 $\frac{\pi d^{4}}{32}$, 중공축의 $I_{p}$는 $\frac{\pi (d^{4} - d_{i}^{4})}{32}$ 입니다.
    $$\frac{T_{A}}{T_{B}} = \frac{I_{pA}}{I_{pB}} = \frac{d^{4}}{d^{4} - (d/2)^{4}}$$
    $$\frac{T_{A}}{T_{B}} = \frac{d^{4}}{d^{4} - \frac{d^{4}}{16}}$$
    $$\frac{T_{A}}{T_{B}} = \frac{16}{15}$$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 250rpm으로 회전하는 축의 끝 저널 베어링(End journal bearing)을 설계하고자 한다. 베어링에 전달되는 하중이 700kgf이고 발열계수가 0.15kgf/mm2 · m/s일 때 저널의 길이에 가장 가까운 값은? (단, π=3이다.)

  1. 60mm
  2. 100mm
  3. 140mm
  4. 200mm
(정답률: 66%)
  • 저널 베어링의 발열계수 공식을 사용하여 저널의 길이를 산출합니다.
    $$P = \frac{W}{L \cdot d} = K \cdot v = K \cdot \frac{\pi d n}{60}$$
    $$L = \frac{W}{K \cdot \frac{\pi d n}{60} \cdot d} = \frac{700 \times 1000}{0.15 \cdot \frac{3 \cdot d \cdot 250}{60} \cdot d}$$
    $$L \approx 60 \text{ mm}$$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 단면 지름이 40mm인 봉에 80N/mm2의 인장응력과 30N/mm2의 전단응력이 동시에 작용할 경우 최대 주응력의 크기는?

  1. 70N/mm2
  2. 80N/mm2
  3. 90N/mm2
  4. 100N/mm2
(정답률: 57%)
  • 인장응력과 전단응력이 동시에 작용할 때의 최대 주응력은 모어 원의 원리를 이용하여 계산합니다.
    $$\sigma_{1} = \frac{\sigma_{x} + \sigma_{y}}{2} + \sqrt{(\frac{\sigma_{x} - \sigma_{y}}{2})^{2} + \tau^{2}}$$
    $$\sigma_{1} = \frac{80 + 0}{2} + \sqrt{(\frac{80 - 0}{2})^{2} + 30^{2}}$$
    $$\sigma_{1} = 90 \text{ N/mm}^{2}$$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 안지름 D1=60mm, 바깥지름 D2=100mm인 원판 클러치가 N=400rpm으로 회전할 때 다음 중 최대 전달토크에 가장 가까운 값은? (단, 마찰계수 μ=0.2, 허용 전달압력 p=1N/mm2, π=3이다.)

  1. 12N · m
  2. 38N · m
  3. 97N · m
  4. 153N · m
(정답률: 70%)
  • 원판 클러치의 최대 전달토크는 마찰면의 평균 압력과 마찰계수를 이용하여 계산합니다.
    ① [기본 공식]
    $$T = \mu \times p \times \frac{\pi D_{2}^{2} - \pi D_{1}^{2}}{4} \times \frac{D_{1} + D_{2}}{2}$$
    ② [숫자 대입]
    $$T = 0.2 \times 1 \times \frac{3 \times 100^{2} - 3 \times 60^{2}}{4} \times \frac{60 + 100}{2}$$
    ③ [최종 결과]
    $$T = 38.4$$
    따라서 가장 가까운 값은 38N · m입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >