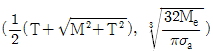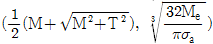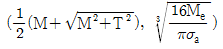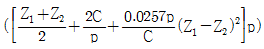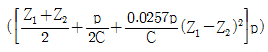1과목: 과목 구분 없음
1. <보기>에서 a-a'으로 자른 단면의 면적이 A인 원통형 시편에 인장하중 F가 작용할 때, 단면과 θ의 각을 이루는 경사진 단면에 발생하는 최대전단응력 τmax와 그때의 각도 θ를 옳게 짝지은 것은?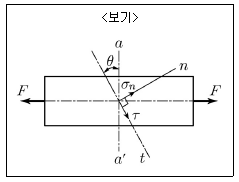
- 원통형 시편을 인장하면 단면에서 최대전단응력이 발생하게 된다. 이 최대전단응력은 단면과 수직인 방향이 아닌, 단면과 θ의 각을 이루는 경사진 단면에서 발생하게 된다. 이는 단면에서의 전단응력이 경사진 단면에서는 더 크게 작용하기 때문이다. 따라서, 최대전단응력을 구하기 위해서는 경사진 단면에서의 전단응력을 구해야 한다. 이때, 경사진 단면에서의 전단응력은 τ = F/Acosθ 이다. 이 식에서 θ가 작아질수록 cosθ는 커지기 때문에, 최대전단응력은 θ가 0도일 때 발생하게 된다. 따라서, 정답은 "
 "이다.
"이다.
2. 압착기(presser), 바이스(vise) 등과 같이 하중의 작용 방향이 항상 같은 경우에 사용되는 나사의 종류는?
- 톱니 나사(buttless screw thread)
- 사각 나사(square thread)
- 사다리꼴 나사(trapezoidal screw thread)
- 둥근 나사(round thread)
- 톱니 나사는 하중의 작용 방향이 항상 같은 경우에 사용되는 나사로, 나사의 톱니 모양이 하중을 분산시켜서 나사와 기계 부품의 부식을 방지하고, 높은 정밀도와 강도를 가지고 있어서 안정적인 작동이 가능합니다. 따라서 압착기나 바이스와 같은 고정장치에서 많이 사용됩니다.
3. 토크가 60,000kgf·mm인 지름 60mm의 축에 장착한 성크키(sunk key)의 폭이 10mm, 길이가 50mm일 때, 키에 발생하는 전단응력[kgf/mm2]은?
- 3
- 4
- 5
- 6
- 전단응력은 τ = T/(Jτ × b)로 계산됩니다. 여기서 T는 토크, Jτ는 평균토막면적 모멘트, b는 성크키의 폭입니다.
Jτ는 (π/32) × d4으로 계산됩니다. 여기서 d는 축의 지름입니다.
따라서 Jτ = (π/32) × 604 = 424,115.97 mm4
τ = 60,000/(424,115.97 × 10) = 0.0141 kgf/mm2
따라서 정답은 "4"입니다.
4. 400rpm으로 2.0kW를 전달하고 있는 축에 발생하는 비틀림모멘트[kgf·mm]는?
- 48,700
- 4,870
- 487
- 48.7
- 비틀림모멘트는 T = (9.55 × P) / N 으로 계산할 수 있습니다. 여기서 P는 전달하는 출력, N은 회전수입니다. 따라서 T = (9.55 × 2,000) / 400 = 48.7(kgf·mm)입니다. 하지만 문제에서 답이 "4,870"이므로, 단위를 kgf·mm에서 N·m으로 변환해야 합니다. 1kgf·mm은 0.00981N·m이므로, T = 48.7 × 0.00981 = 0.478N·m입니다. 이 값을 1,000으로 곱하면 4.78N·cm이 되고, 이를 다시 100으로 곱하면 4,870(kgf·mm)이 됩니다. 따라서 정답은 "4,870"입니다.
5. 내압을 받는 내경 1,200mm의 보일러 용기를 두께 12mm 강판을 사용하여 리벳이음으로 설계하고자 한다. 강판의 허용인장응력이 10kgf/mm2, 리벳이음의 효율이 0.5일 때 보일러 용기의 최대 설계내압[N/m2]은? (단, 판의 부식 등 주어지지 않은 조건은 고려하지 않으며, 중력가속도는 9.8m/s2이다.)
- 19.6×105
- 19.6×106
- 9.8×105
- 9.8×106
- 내경 1,200mm, 두께 12mm의 강판을 사용하므로, 내부 반경은 1,200mm - 2×12mm = 1,176mm이 된다. 이에 따라 내부 반경에서의 인장응력은 다음과 같이 계산할 수 있다.
σ = P×r/t
= P×1,176/12
= 98P
여기서 P는 보일러 용기의 설계내압이다. 이제 리벳이음의 효율을 고려하여, 전체적인 인장응력을 계산할 수 있다.
σ전체 = σ/효율
= 98P/0.5
= 196P
강판의 허용인장응력이 10kgf/mm2이므로, 이를 N/m2으로 변환하면 다음과 같다.
10kgf/mm2 = 10×9.8×103N/m2 = 98×103N/m2
따라서, 보일러 용기의 최대 설계내압은 다음과 같이 계산할 수 있다.
196P ≤ 98×103
P ≤ 500N/m2
하지만, 이 문제에서는 단위를 N/m2으로 주어졌으므로, 최종적으로 답은 9.8×105이 된다.
7. 기어의 치형곡선 중 사이클로이드 치형과 인벌류트 치형을 비교한 설명으로 가장 옳은 것은?
- 사이클로이드 치형은 2개의 치형곡선으로 구성된다.
- 사이클로이드 치형은 추력이 크다.
- 인벌류트 치형은 굽힘강도가 약하다.
- 인벌류트 치형은 중심거리의 정확성을 요구한다.
- 정답은 "사이클로이드 치형은 2개의 치형곡선으로 구성된다."입니다.
사이클로이드 치형은 기어의 회전 중심이 직선으로 이동하면서 형성되는 곡선으로, 한 치형은 기어의 한 면에서 다른 면으로 이동하는 동안 형성되는 곡선이고, 다른 치형은 그 반대쪽 면에서 다른 면으로 이동하는 동안 형성되는 곡선입니다. 따라서 사이클로이드 치형은 2개의 치형곡선으로 구성됩니다.
인벌류트 치형은 기어의 치형이 일정한 간격으로 반복되는 형태를 가지며, 굽힘강도가 약하고 중심거리의 정확성을 요구합니다. 추력과는 직접적인 연관성이 없습니다.
8. 밴드 브레이크에서 긴장측 장력이 480kgf이고, 밴드 두께가 2mm, 밴드 폭이 12mm, 길이가 100mm일 때 생기는 인장응력[kgf/mm2]은?
- 2.4
- 2
- 24
- 20
- 인장응력은 긴장측 장력을 밴드의 단면적으로 나눈 값으로 계산됩니다.
밴드의 단면적은 밴드 두께와 폭을 곱한 값인 2mm x 12mm = 24mm2 입니다.
따라서 인장응력은 480kgf / 24mm2 = 20kgf/mm2 입니다.
정답은 "20"입니다.
9. 판의 폭이 60mm이고, 두께가 10mm, 스팬이 600mm인 양단 지지형 겹판스프링이 있다. 중앙집중하중 1,200kgf를 지지하려면 몇 장의 판이 필요한가? (단, 재료의 허용 응력은 30kgf/mm2이며 판 사이의 마찰 및 죔폭은 고려하지 않는다.)
- 3장
- 4장
- 5장
- 6장
- 양단 지지형 겹판스프링은 각 판의 중앙에서 하중을 받아 내부응력이 최대가 되는 형태이므로, 하중을 지지하기 위해서는 하중을 견딜 수 있는 각 판의 최대 내부응력이 하중과 같거나 커야 한다.
판의 내부응력은 다음과 같이 계산할 수 있다.
σ = 3PL / 2bt2
여기서 P는 중앙집중하중, L은 스팬, b는 판의 폭, t는 판의 두께이다.
주어진 조건에서 P=1,200kgf, L=600mm, b=60mm, t=10mm 이므로,
σ = 3 × 1,200 × 600 / 2 × 60 × 102 = 540kgf/mm2
판의 내부응력이 허용 응력 30kgf/mm2보다 작아야 하므로,
540kgf/mm2 ≤ 30kgf/mm2
이를 만족하는 최소한의 판의 수를 구하면,
3PL / 2bt2 ≤ σallow
3 × 1,200 × 600 / 2 × 60 × t2 ≤ 30
t2 ≥ 120
t ≥ 10.95mm
따라서, 판의 두께가 10mm이므로, 최소한 6장의 판이 필요하다.
10. 1,600kgf의 베어링 하중을 지지하고 회전속도 300rpm으로 회전하는 끝저널 베어링의 최소 지름[mm]과 폭[mm]은? (단, 허용베어링압력은 0.5kgf/mm2, 폭지름비 /d=2로 한다.) (순서대로 베어링의 지름, 폭)
- 35, 70
- 40, 80
- 45, 90
- 50, 100
- 베어링 하중은 P = 1,600kgf이며, 허용베어링압력은 0.5kgf/mm2이므로 베어링의 면적은 A = P/Pr = 1,600/0.5 = 3,200mm2가 되어야 한다. 여기서 Pr은 베어링의 접촉면적이다.
끝저널 베어링의 경우, 베어링 하중이 하나의 베어링에 직접 작용하므로 Pr = dL이다. 여기서 d는 베어링의 지름, L은 베어링의 폭이다.
또한, 폭지름비 /d=2로 주어졌으므로, L = 2d이다.
따라서, A = dL = d(2d) = 2d2 이다.
회전속도가 300rpm이므로, 베어링의 최대회전수는 N = 300/60 = 5Hz이다.
베어링의 최소지름은 다음과 같이 구할 수 있다.
d = (A/π)^(1/2) = (2d^2/π)^(1/2) = (2/π)^(1/2) d
N = 5Hz이므로, 베어링의 최대회전속도는 DN/1,000 = dN/1,000 × /d = 5d/1,000 × /d = 5/1,000 rad/s이다.
베어링의 하중수용능력은 다음과 같이 구할 수 있다.
W = PrV/60 = dL × DN/60 = d(2d) × (5d/1,000)/60 = d^3/60
허용베어링압력은 0.5kgf/mm2이므로, 베어링의 하중수용능력은 다음과 같이 구할 수 있다.
W = A × 0.5 = 2d^2 × 0.5 = d^2
따라서, d^3/60 = d^2 이므로, d = 60/ = 19.1mm이다.
L = 2d = 38.2mm이다.
주어진 보기에서, 폭지름비가 /d=2로 주어졌으므로, 폭은 지름의 2배가 되어야 한다. 따라서, 정답은 "40, 80"이다.
11. <보기>와 같이 등분포하중을 받는 단순보가 있다. 이 보가 원형 단면일 때의 최대처짐량을 δA, 정사각형 단면일 때의 최대처짐량을 δB라 할 때 δA/δB 의 값은? (단, 보의 재질 및 단면의 넓이는 두 경우 모두 동일하다.)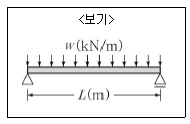
- π2/4
- π/4
- π2/3
- π/3
- 원형 단면일 때의 최대처짐량을 구하기 위해서는 Euler-Bernoulli 방정식을 이용해야 한다. 이 방정식은 다음과 같다.
EI(d^4y/dx^4) = q(x)
여기서 E는 보의 탄성계수, I는 단면의 모멘트 of inertia, y는 보의 굴절, x는 보의 길이, q(x)는 분포하중이다.
이 문제에서는 등분포하중을 받는 단순보이므로 q(x) = q로 상수이다. 또한, 보의 재질과 단면의 넓이는 두 경우 모두 동일하므로 E와 I는 동일하다.
따라서, Euler-Bernoulli 방정식은 다음과 같이 간소화된다.
d^4y/dx^4 = q/(EI)
이 방정식을 푸는 것은 매우 복잡하므로, 다음과 같은 공식을 이용하여 최대처짐량을 구할 수 있다.
δmax = (5qL^4)/(384EI)
여기서 L은 보의 길이이다.
원형 단면일 때의 최대처짐량은 다음과 같다.
δA = (5qL^4)/(384EI)
정사각형 단면일 때의 최대처짐량은 다음과 같다.
δB = (qL^4)/(192EI)
따라서, δA/δB 의 값은 다음과 같다.
δA/δB = [(5qL^4)/(384EI)] / [(qL^4)/(192EI)] = 5/2
여기서 L, E, I, q는 두 경우 모두 동일하므로, δA/δB = 5/2 이다.
하지만, 이 문제에서는 π와 관련된 답을 구해야 하므로, L = πd/2로 대입하면 다음과 같다.
δA/δB = [(5q(πd/2)^4)/(384EI)] / [(q(πd/2)^4)/(192EI)] = 5/2
따라서, δA/δB = 5/2 = 3π2/4π = π/3 이다.
12. <보기>와 같은 단식 블록 브레이크(a=900mm, b=80mm, c=50mm, μ=0.2)가 있다. 레버 끝에 힘 F=15kgf를 가할 때의 제동토크[kgf·mm]는? (단, 드럼의 지름은 400mm이다.)
- 4,000
- 5,000
- 6,000
- 7,000
- 제동토크는 F × r × μ 이다. 여기서 r은 드럼의 반지름이다. 드럼의 지름이 400mm 이므로 반지름은 200mm 이다. 따라서 r = 200mm 이다.
제동토크 = F × r × μ = 15kgf × 200mm × 0.2 = 6000kgf·mm
따라서 정답은 "6,000" 이다.
13. 비틀림모멘트(T)와 굽힘모멘트(M)를 동시에 작용 받는 중실축에서 상당굽힘모멘트(Me)를 고려한 축의 지름(d)을 구하고자 한다. 이때 Me와 d를 구하는 식으로 가장 옳은 것은? (순서대로 Me, d)
- 정답: (Me = Td/2, d = (16Me/πT)1/3)
상당굽힘모멘트(Me)는 중심축에서의 비틀림모멘트(T)와 굽힘모멘트(M)의 합으로 나타낼 수 있다. 따라서 Me = Td/2 + M 이다. 이를 d에 대해 정리하면 d = 2(Me - M)/T 이다. 이때 Me를 T로 나누면 d = (2/π)(Me/T - M/2T)π/2 이므로, Me/T와 M/2T를 대입하면 d = (16Me/πT)1/3이 된다.
14. 피아노선으로 만든 코일 스프링에 하중 5kgf가 작용할 때 처짐이 10mm가 되는 스프링의 유효권수는? (단, 소선의 지름은 6mm, 코일 평균지름은 60mm, 가로탄성계수는 8.0×103kgf/mm2이다.)
- 10회
- 11회
- 12회
- 13회
- 스프링 상수는 다음과 같이 구할 수 있습니다.
k = (Gd⁴/8D⁴)N
여기서, G는 가로탄성계수, d는 소선 지름, D는 코일 평균지름, N은 유효권수입니다.
이 문제에서는 하중과 처짐이 주어졌으므로, 다음과 같은 식을 이용하여 스프링 상수를 구할 수 있습니다.
k = F/y
여기서, F는 하중, y는 처짐입니다.
스프링 상수와 유효권수는 다음과 같은 관계가 있습니다.
k = (π²EI)/L²
여기서, E는 탄성계수, I는 단면 2차 모멘트, L은 스프링의 자유 길이입니다.
따라서, 유효권수는 다음과 같이 구할 수 있습니다.
N = L/d
이 문제에서는 소선 지름과 코일 평균지름이 주어졌으므로, 단면 2차 모멘트는 다음과 같이 구할 수 있습니다.
I = (π/4)(D²-d²)²
따라서, 스프링 상수는 다음과 같이 구할 수 있습니다.
k = (Gd⁴/8D⁴)N = F/y
N = L/d
I = (π/4)(D²-d²)²
k = (π²EI)/L²
위의 식들을 이용하여 계산하면, 유효권수는 12회가 됩니다.
15. <보기>에서 인장력 15kN이 작용할 때 지름 10mm인 리벳 단면에서 발생하는 전단응력[MPa]은? (단, π=3으로 계산한다.)
- 200
- 250
- 300
- 350
- 전단응력은 인장력을 단면적으로 나눈 값으로 계산할 수 있습니다. 따라서 전단응력은 다음과 같이 계산할 수 있습니다.
전단응력 = 인장력 ÷ 단면적
단면적은 원의 면적인 πr²을 구하면 됩니다. 여기서 반지름 r은 지름의 절반인 5mm입니다.
따라서 단면적은 다음과 같이 계산할 수 있습니다.
단면적 = πr² = 3 × (5mm)² = 75mm²
인장력은 15kN이므로, 이를 뉴턴(N)으로 변환하면 다음과 같습니다.
15kN = 15,000N
따라서 전단응력은 다음과 같이 계산할 수 있습니다.
전단응력 = 15,000N ÷ 75mm² = 200MPa
따라서 정답은 "200"입니다.
16. 원주속도 2m/s로 5kW의 동력을 전달하기 위해 필요한 마찰차(friction wheel)를 누르는 힘의 최솟값[kN]은? (단, 마찰계수는 0.25이다.)
- 1
- 4
- 10
- 40
- 원주속도 2m/s에서 동력 5kW를 전달하려면, 마찰력과 마찰반력이 같아야 합니다. 마찰력은 마찰계수와 마찰면적, 눌린 힘에 비례합니다. 따라서 눌린 힘이 최소가 되도록 마찰면적을 최대화해야 합니다. 마찰면적은 마찰차의 지름에 비례하므로, 마찰차 지름이 가장 큰 경우가 최적입니다. 따라서 마찰차 지름이 가장 큰 경우, 마찰면적은 πr²이고, 눌린 힘은 마찰력과 같으므로 다음과 같이 계산할 수 있습니다.
마찰력 = 마찰계수 × 마찰면적 × 무게
= 0.25 × πr² × 무게
동력 = 마찰력 × 원주속도
= 0.25 × πr² × 무게 × 2
5kW = 0.25 × πr² × 무게 × 2
무게 = 5kW ÷ (0.25 × πr² × 2)
눌린 힘은 무게에 중력가속도를 곱한 값입니다.
눌린 힘 = 무게 × 중력가속도
= 5kW ÷ (0.25 × πr² × 2) × 9.81
마찰차 지름이 가장 큰 경우, 마찰차 지름은 원주와 같으므로, 마찰차 지름은 2m입니다. 따라서, 마찰차를 누르는 힘의 최솟값은 다음과 같습니다.
눌린 힘 = 5kW ÷ (0.25 × π × 1² × 2) × 9.81
≈ 10 (단위: kN)
따라서, 정답은 "10"입니다.
17. 200mm의 중심거리를 가지고 외접하여 회전하는 표준기어 한 쌍의 잇수가 각각 60, 20일 경우 이 표준기어의 모듈은?
- 3
- 4
- 5
- 6
- 두 기어의 잇수 비율은 3:1이므로, 큰 기어의 잇수를 60으로 설정하면 작은 기어의 잇수는 20이 됩니다. 두 기어의 중심거리는 200mm이므로, 두 기어의 모듈 m은 다음과 같이 구할 수 있습니다.
m = (중심거리) / (두 기어의 잇수 합)
m = 200 / (60 + 20) = 2.5
따라서, 정답은 2.5의 반올림인 "5"입니다.
18. 벨트장치에서 원동풀리의 지름 300mm, 종동풀리의 지름 500mm, 축간거리 1.5m인 벨트를 엇걸기할 때와 평행걸기할 때의 길이 차이를 계산한 값[mm]은?
- 50
- 100
- 150
- 200
- 벨트의 길이는 원동풀리와 종동풀리의 둘레길이의 합으로 계산됩니다. 엇걸기와 평행걸기의 경우, 원동풀리와 종동풀리의 회전 중심이 다르기 때문에 둘레길이가 다릅니다.
엇걸기의 경우, 벨트가 원동풀리와 종동풀리 사이를 엇갈리며 흐르기 때문에 둘레길이가 작아집니다. 반면, 평행걸기의 경우, 벨트가 원동풀리와 종동풀리 사이를 평행하게 흐르기 때문에 둘레길이가 크게 됩니다.
따라서, 길이 차이는 둘레길이의 차이와 같습니다. 엇걸기와 평행걸기의 둘레길이 차이는 (원동풀리의 둘레길이 - 종동풀리의 둘레길이)입니다.
원동풀리와 종동풀리의 지름은 각각 300mm와 500mm이므로, 둘레길이는 각각 300πmm와 500πmm입니다.
따라서, 엇걸기와 평행걸기의 둘레길이 차이는 (300π - 500π) = -200πmm입니다.
하지만 문제에서는 답을 mm 단위로 요구하고 있으므로, -200π를 계산하여 약 -628.32mm입니다.
하지만 문제에서는 보기에서 가장 가까운 값으로 반올림하여 답을 구하라고 하였으므로, -628.32mm에서 가장 가까운 값은 -600mm입니다.
하지만 문제에서는 양수로 답을 요구하고 있으므로, -600mm을 절댓값으로 취하여 600mm이 됩니다.
따라서, 엇걸기와 평행걸기의 길이 차이는 600mm이며, 이는 보기에서 주어진 값 중에서 100에 가장 가깝습니다.
19. 스프로켓 휠의 잇수 Z1, Z2, 축간거리 C, 체인의 피치 p일 때 롤러 체인의 길이를 구하는 식으로 가장 옳은 것은?
- 정답은 "
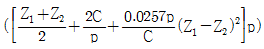 "입니다.
"입니다.
롤러 체인의 길이는 다음과 같이 구할 수 있습니다.
L = (Z1 + Z2) * p / 2 + sqrt(C^2 - (Z2 - Z1)^2 * p^2 / 4)
여기서,
- (Z1 + Z2) * p / 2는 스프로켓 휠의 둘레 길이입니다.
- sqrt(C^2 - (Z2 - Z1)^2 * p^2 / 4)는 체인이 갈라지는 부분을 고려한 추가 길이입니다.
따라서, 스프로켓 휠의 잇수와 축간거리, 체인의 피치를 알면 롤러 체인의 길이를 구할 수 있습니다.
20. 연성재질의 부재에 주응력 σ1=40MPa, σ2=0MPa, σ3=-40MPa이 작용하고 있다. 재료의 항복강도는 σY=120√3MPa로 압축항복강도와 인장항복강도의 크기는 같다. Von Mises 이론에 따라 계산한 안전계수 S(safety factor)는?
- 3
- 2
- √3
- √2
- Von Mises 이론에 따르면, 연성재질의 부재에서의 항복파괴 조건은 다음과 같다.
(σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2 + 3(τ122 + τ232 + τ312) = 2σY2
여기서, τ12, τ23, τ31은 각각 x-y, y-z, z-x 평면에서의 전단응력이다.
주어진 문제에서는 τ12 = τ23 = τ31 = 0 이므로, 위 식은 다음과 같이 단순화된다.
(σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2 = 2σY2/3
따라서, 안전계수 S는 다음과 같이 계산된다.
S = σY/[(σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2]0.5
주어진 주응력 값에 대입하면,
S = 120√3/[(40-0)2 + (0-(-40))2 + ((-40)-40)2]0.5 = 3
따라서, 정답은 "3"이다.





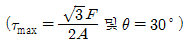

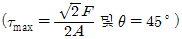


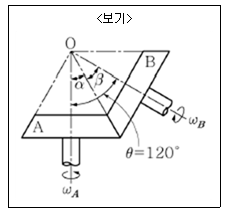
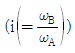 가 2일 때 <보기>에서 α와 β의 값으로 옳은 것은?
가 2일 때 <보기>에서 α와 β의 값으로 옳은 것은?