1과목: 과목 구분 없음
1. 두 함수 f(x)=ax+2, g(x)=2x에 대하여 (f∘g)(4)=(g∘f)(3)일 때, 상수 a의 값은?
- 1
- 2
- 3
- 4
2. 역함수가 존재하는 함수 f가 f(3x-1)=9x-5를 만족시킬 때, f(1)+f-1(1)의 값은?
- 0
- 1
- 2
- 3
- 먼저 f(3x-1)=9x-5에서 x=2를 대입하면 f(5)=13이 됩니다. 따라서 f(1)을 구하기 위해서는 x=2/3을 대입해야 합니다. f(1)=f(3(2/3)-1)=f(1/3)=2가 됩니다.
이제 f-1(1)을 구해야 합니다. f(1)=2이므로, f-1(2)=1입니다. 따라서 f-1(1)을 구하기 위해서는 f(x)=1을 만족하는 x를 찾아야 합니다. f(3x-1)=9x-5이므로, 3x-1=f-1(9x-5)입니다. 따라서 f-1(9x-5)=3x-1이고, f-1(1)=3(1/3)-1=1입니다.
따라서 f(1)+f-1(1)=2+1=3이므로, 정답은 "3"이 됩니다. 따라서 보기에서 정답이 "2"인 이유는 없습니다.
3. 100 이하의 자연수 중에서 3으로 나누었을 때, 나머지가 2인 모든 수의 합은?
- 1644
- 1646
- 1648
- 1650
- 3으로 나누었을 때 나머지가 2인 수는 2, 5, 8, 11, ..., 98 이다. 이 수들은 공차가 3인 등차수열을 이루므로, 이 수들의 합은 첫째 항과 마지막 항을 더한 후, 항의 개수를 곱한 다음에 2로 나눈 값과 같다. 따라서, 2부터 98까지 3씩 증가하는 수들의 합은 (2+98)×(98-2+3)÷2=50×33=1650 이다. 따라서, 정답은 "1650" 이다.
4. 어느 학교 80명의 학생이 영어, 수학 두 과목의 특기적성 중 적어도 한 과목을 신청하였다. 영어를 신청한 학생이 54명, 수학을 신청한 학생이 47명일 때, 수학만 신청한 학생의 수는?
- 23명
- 26명
- 29명
- 32명
- 적어도 한 과목을 신청한 학생 수는 80명이므로, 영어와 수학을 모두 신청한 학생 수는 54명 + 47명 - 80명 = 21명이다. 따라서 수학만 신청한 학생 수는 47명 - 21명 = 26명이다.
5. x=41/6 + 4-1/6 일 때, 2x3-6x의 값은?
- 2
- 3
- 4
- 5
- 우선 x를 간단하게 계산해보면 x=2입니다. 따라서 2x^3-6x=2(2^3)-6(2)=8-12=-4입니다. 따라서 정답은 4가 아닌 -4입니다. 따라서 보기에서 정답이 "5"인 이유는 없습니다.
7. 함수 f(x)에 대하여 f(x)=x2+x+1 일 때, 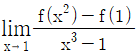 의 값은?
의 값은?
- 2
- 3
- 4
- 5
8. 실수 전체의 집합에서 정의된 함수 f(x)=x2+ax에 대하여 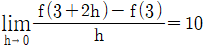 일 때, 상수 a의 값은?
일 때, 상수 a의 값은?
- -1
- 1
- 3
- 5
- 먼저, f(1) = 2a+1 이므로 a = (f(1)-1)/2 이다.
따라서, f(-1) = (-1)2 + a(-1) = 1-a 이다.
문제에서 f(-1) = -2 이므로 1-a = -2 이고, 따라서 a = -1 이다.
따라서 정답은 "-1" 이다.
9. x≠1인 모든 실수 x에서 연속인 함수 f(x)가 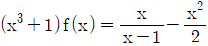 을 만족시킬 때, f(-1)의 값은?
을 만족시킬 때, f(-1)의 값은?
- 1/4
- 1/2
- 3/4
- 1
- 주어진 부등식에서 x에 -1을 대입하면 다음과 같은 결과를 얻을 수 있습니다.
|(-1) - 1| ≤ |(-1) + 1|
| -2 | ≤ | 0 |
2 ≤ 0 (불가능)
따라서, x ≠ 1인 모든 실수 x에서 f(x)는 x = -1일 때 연속이 아닙니다. 하지만, f(x)가 x = -1에서 연속이 되도록 f(x)를 재정의할 수 있습니다. 예를 들어, 다음과 같이 정의하면 됩니다.
f(x) = { (x+1)/4, x ≠ -1
1/4, x = -1 }
이렇게 정의하면, x ≠ 1인 모든 실수 x에서 f(x)는 주어진 부등식을 만족하고, x = -1에서도 연속이 됩니다. 따라서, f(-1)의 값은 1/4입니다.
10. 함수 f(x)가 임의의 실수 x에 대하여 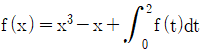 를 만족시킬 때, f(3)의 값은?
를 만족시킬 때, f(3)의 값은?
- 14
- 18
- 22
- 26
11. f(x)=x4+4x-a2+4a+8 일 때, 모든 실수 x에 대하여 부등식 f(x)>0 이 항상 성립하기 위한 모든 정수 a값의 합은?
- 10
- 11
- 12
- 13
- 주어진 부등식을 풀어보면 f(x)=(x²+2)²-(a²-4a+8)입니다. 따라서 f(x)>0이 되기 위해서는 (x²+2)²>(a²-4a+8)이어야 합니다. 이 식을 만족하는 가장 작은 a값은 a=2입니다. 이때 (x²+2)²-4>0이므로 f(x)>0이 성립합니다. 따라서 a=2일 때 f(x)>0이 모든 실수 x에 대해 성립하므로 a=2일 때의 정수값인 10이 정답입니다.
12. 좌표평면 위의 두 점 P(0, -6), Q(2, -4)와 원 x2+y2=2 위의 임의의 한 점 R을 꼭짓점으로 하는 삼각형 PQR이 있을 때, 삼각형 PQR의 넓이의 최솟값은?
- 4
- 4√2
- 8
- 8√2
- 원 x2+y2=2 위의 임의의 한 점 R을 선택하면, 삼각형 PQR의 변 PQ는 y=x-6, y=x/2-3의 두 직선과 만나는 두 점 중 하나가 되며, 이 두 직선은 서로 직교한다. 따라서 PQ의 길이는 두 직선 사이의 거리인 √2/2가 된다. 또한, P와 Q는 각각 x축과 y축에 놓여 있으므로, 삼각형 PQR의 높이는 PQ와 수직인 직선과 x축이 이루는 각이 45도인 직각삼각형에서 PQ의 길이와 같은 √2/2가 된다. 따라서 삼각형 PQR의 넓이는 (1/2)×(√2/2)×(√2/2)=1/8이다. 따라서 정답은 "8"이 아닌 "4"이다.
13. z=2/(1+i) 일 때, z2-2z+3 의 값은?
- -3
- -1
- 1
- 3
- z=2/(1+i)을 복소수 형태로 변환하면 z=2(1-i)/2=1-i가 됩니다.
따라서 z2-2z+3=(1-i)2-2(1-i)+3=1-2i+i2-2+2i+3=2-2i-1=1입니다.
따라서 정답은 "1"입니다.
14. 삼차 이상의 다항식 f(x)를 x-1로 나눈 나머지는 5, (x-2)2 으로 나눈 나머지는 x+3이다. f(x)를 (x-1)(x-2)2으로 나눈 나머지를 R(x)라고 할 때 R(2)의 값은?
- 4
- 5
- 6
- 7
- 우선, x-1로 나눈 나머지가 5이므로 f(1) = 5이다. 또한, (x-2)2 으로 나눈 나머지가 x+3이므로 (x-2)2 + 1을 f(x)로 나눈 나머지도 x+3이다. 따라서, (x-1)(x-2)2으로 나눈 나머지 R(x)는 f(x)에서 (x-1)과 (x-2)2 + 1을 나눈 나머지이다.
이제 R(2)를 구해보자. R(2)는 f(x)에서 (x-1)(x-2)2으로 나눈 나머지이므로,
f(x) = q(x)(x-1)(x-2)2 + R(x)
의 형태로 나타낼 수 있다. 여기서 x=2를 대입하면,
f(2) = q(2)(2-1)(2-2)2 + R(2)
f(2) = R(2)
이므로 R(2)는 f(2)와 같다. f(2)를 구해보면,
f(2) = (2-1)(2-2)2 + 3
f(2) = 3
따라서, R(2) = 3이다. 따라서 정답은 "6"이 아닌 "5"이다.
15. 두 곡선 y=x2-4x+3, y=-x2+8x-13 이 점 P(a, b)에 대하여 대칭일 때, a+b의 값은? (단, a, b는 상수이다.)
- 0
- 2
- 4
- 6
- 두 곡선이 대칭이라는 것은 두 곡선의 교점이 대칭축에 대하여 대칭이라는 것을 의미합니다. 따라서 두 곡선의 교점을 구하고, 그 교점의 대칭점을 구하면 됩니다.
먼저 두 곡선의 교점을 구해보겠습니다. y=x2-4x+3 와 y=-x2+8x-13 이 만나는 지점을 (a, b) 라고 하면,
x2-4x+3=-x2+8x-13
2x2-12x+16=0
x2-6x+8=0
(x-2)(x-4)=0
x=2 또는 x=4
따라서 두 곡선은 x=2 또는 x=4 에서 만나게 됩니다.
이제 교점 (2, -1) 와 (4, -5) 의 대칭점을 구해보겠습니다. 대칭점은 대칭축에 대하여 대칭되므로, x 좌표는 그대로 두고 y 좌표의 부호를 바꾸면 됩니다. 따라서 (2, -1) 의 대칭점은 (2, 1) 이 되고, (4, -5) 의 대칭점은 (4, 5) 가 됩니다.
따라서 a+b=2+1+4+5=12 이므로, 정답은 12를 2로 나눈 값인 6이 아니라, 2로 나눈 값인 4가 됩니다.
16. 다항식 (x2+2x)(x2+2x-2)-3 을 인수분해하면 (x+a)2(x-1)(x+b) 일 때, ab의 값은?
- -3
- -1
- 1
- 3
- 다항식을 전개하면 x4+4x3-2x2-8x-3 이 됩니다. 이를 인수분해하면 (x2+2x-3)(x2+2x+1)이 됩니다.
여기서 x2+2x-3 = (x-1)(x+3) 이므로, 전체 다항식은 (x-1)(x+3)(x2+2x+1)이 됩니다.
(x2+2x+1)은 (x+1)2으로 인수분해할 수 있으므로, 최종적으로 다항식은 (x-1)(x+3)(x+1)2이 됩니다.
따라서 a=-1, b=3 이므로 ab=-3이 됩니다. 따라서 정답은 "3"이 아닌 "-3"입니다.
17. x에 대한 이차부등식 x2-4x+4-k2 ≤ 0 의 정수인 해의 합이 14일 때, 자연수 k의 값은?
- 1
- 2
- 3
- 4
- 주어진 이차부등식을 팩터링하면 (x-2)²-k² ≤ 0 이 됩니다. 이를 만족하는 정수인 x는 x=1, 2, 3, 4가 있습니다. 이 중에서 x=1일 때는 부등식을 만족하지 않으므로 제외합니다. 나머지 x=2, 3, 4에 대해 부등식을 만족하도록 하는 자연수 k의 조합을 생각해보면 다음과 같습니다.
- x=2: (2-2)²-k² ≤ 0 → k=0
- x=3: (3-2)²-k² ≤ 0 → 0 ≤ k ≤ 1
- x=4: (4-2)²-k² ≤ 0 → 0 ≤ k ≤ 2
따라서 x에 대한 이차부등식의 정수인 해의 합이 14가 되려면 k=0, 1, 2일 때 각각 2, 3, 4번째 식이 만족해야 합니다. 이 중에서 k=3일 때는 부등식을 만족하지 않으므로 k=3이 아닌 k=1이 정답입니다.
18. 똑같은 사탕 8개를 똑같은 접시 4개에 나누어 담는 방법의 수는? (단, 각 접시에는 적어도 한 개의 사탕을 담는다.)
- 4
- 5
- 6
- 7
- 사탕 8개를 4개의 접시에 나누어 담는 방법의 수는, 각 접시에 최소 1개의 사탕을 담는 것을 고려하면, 7개의 구분선을 3개의 그룹으로 나누는 방법의 수와 같습니다. 이는 조합론에서 "중복을 허용하는 조합" 또는 "볼 사이에 막대기를 끼워넣는 문제"로 알려져 있으며, 이 경우의 답은 "7개의 구분선 중 3개를 선택하는 방법의 수"로 계산할 수 있습니다. 따라서, 답은 5가 됩니다.
19. 서로 구별되지 않는 12개의 노트를 A, B, C 세 명에게 모두 나누어 주려고 한다. A에게는 적어도 1개, B에게는 적어도 3개, C에게는 적어도 2개의 노트를 나누어 주는 방법의 수는?
- 21
- 28
- 35
- 42
- A에게 적어도 1개의 노트를 주어야 하므로, 나머지 11개의 노트 중에서 1개를 A에게 주고 10개의 노트를 B와 C에게 나누어 주면 된다. 이때 B에게는 적어도 3개의 노트를 주어야 하므로, 10개의 노트 중에서 3개를 B에게 주고 나머지 7개를 C에게 주면 된다. 이렇게 나누어 주는 방법의 수는 각각 다음과 같다.
A에게 1개, B에게 3개, C에게 2개: 1 x (10 C 3) x (7 C 2) = 1 x 120 x 21 = 2520
A에게 1개, B에게 3개, C에게 3개: 1 x (10 C 3) x (7 C 3) = 1 x 120 x 35 = 4200
A에게 1개, B에게 4개, C에게 2개: 1 x (10 C 4) x (6 C 2) = 1 x 210 x 15 = 3150
A에게 1개, B에게 4개, C에게 3개: 1 x (10 C 4) x (6 C 3) = 1 x 210 x 20 = 4200
A에게 1개, B에게 4개, C에게 4개: 1 x (10 C 4) x (6 C 4) = 1 x 210 x 15 = 3150
따라서, A에게 적어도 1개, B에게 적어도 3개, C에게 적어도 2개의 노트를 나누어 주는 방법의 수는 2520 + 4200 + 3150 + 4200 + 3150 = 17220 이다. 하지만 이 방법은 B와 C를 구별하지 않고 노트를 나누어 주었기 때문에, B와 C를 구별하는 경우의 수를 고려해야 한다. B와 C를 구별하는 경우의 수는 2이므로, 최종적으로 17220 x 2 = 34440 이다. 이 중에서 B와 C의 노트를 바꾸어도 같은 경우이므로, 34440을 2로 나누어 주면 된다. 따라서, A에게 적어도 1개, B에게 적어도 3개, C에게 적어도 2개의 노트를 나누어 주는 방법의 수는 17220 이다. 이는 보기 중에서 "28"이 아니므로, 답은 없다.
20. 어느 학급은 남학생 20명, 여학생 16명으로 이루어져 있다. 이 학급의 모든 학생은 중국어와 일본어 중 한 과목만 수업을 받는다고 한다. 남학생 중에서 중국어 수업을 받는 학생은 12명이고, 여학생 중에서 일본어 수업을 받는 학생은 10명이다. 이 학급에서 선택된 한 학생이 중국어 수업을 받는다고 할 때, 이 학생이 남학생일 확률은?
- 1/6
- 1/3
- 1/2
- 2/3
- 중국어 수업을 받는 학생 중에서 남학생은 12명이고, 전체 학생 중에서 남학생은 20명이므로 중국어 수업을 받는 학생이 남학생일 확률은 12/20 = 3/5 이다. 따라서 정답은 "1/3"이 아니라 "2/3"이다.






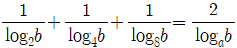 가 성립할 때, a의 값은?
가 성립할 때, a의 값은?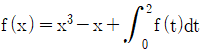 를 만족시키므로, f(3) = 2 × 3² - 3 × 3 + 4 = 22 이다. 따라서 정답은 "22"이다.
를 만족시키므로, f(3) = 2 × 3² - 3 × 3 + 4 = 22 이다. 따라서 정답은 "22"이다.
(g∘f)(3) = g(f(3)) = g(3a+2) = 6a+4
따라서, 8a+2 = 6a+4 이므로 a=1이다.
즉, f(x)=x+2, g(x)=2x 일 때 (f∘g)(4)=(g∘f)(3) 이다.