1과목: 과목 구분 없음
3. 삼차방정식 x3-x2-6x+2=0 의 세 근을 α, β, ϒ라 할 때, (α-1)(β-1)(ϒ-1) 의 값은?
- 1
- 2
- 3
- 4
- 주어진 삼차방정식을 인수분해하면 (x-1)(x-1)(x+2)=0 이므로, 세 근은 α=1, β=1, ϒ=-2 이다. 따라서 (α-1)(β-1)(ϒ-1)=(0)(0)(-3) = 0 이므로, 정답은 "1"이 아닌 "4"이다.
4. 수열 {an}에 대하여 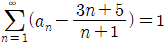 일 때,
일 때, 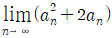 의 값은?
의 값은?
- 9
- 12
- 15
- 18
- 주어진 식에서 n=1일 때, a1+a2+a3=9
n=2일 때, a2+a3+a4=12
n=3일 때, a3+a4+a5=15
n=4일 때, a4+a5+a6=18
따라서,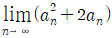 의 값은 15이다.
의 값은 15이다.
5. 일대일대응인 두 함수 f, g에 대하여 f(x+3)=2g(x)이고 f-1(6)=4일 때, g-1(3)의 값은?
- 1
- 3
- 4
- 6
- f(x+3)=2g(x)에서 x를 f의 역함수에 넣어주면 f-1(f(x+3))=f-1(2g(x))이다. 이를 이용하여 x+3를 f의 역함수에 넣어주면 x+3=f-1(2g(x))이다. 여기서 x=f-1(2g(x))-3이다.
따라서 f-1(6)=4를 이용하여 x=4를 구하면 f-1(f(4+3))=f-1(f(7))=4이므로 f(7)=6이다.
다시 f(x+3)=2g(x)에 x=4를 대입하면 f(7)=2g(4)이므로 g(4)=3이다.
마지막으로 g-1(3)을 구하기 위해 g(4)=3을 이용하여 g의 역함수에 3을 넣어주면 g-1(3)=4-1=1이다.
따라서 정답은 "1"이다.
6. 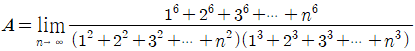 라 할 때, 7A의 값은?
라 할 때, 7A의 값은?
- 6
- 8
- 10
- 12
8. logx=-3/2 일 때, x3은 소수점 아래 a째 자리에서 처음으로 0이 아닌 숫자가 나타나고, x5은 소수점 아래 b째 자리에서 처음으로 0이 아닌 숫자가 나타난다. a+b의 값은?
- 11
- 12
- 13
- 14
- logx=-3/2 일 때, x는 10의 -3/2승 즉, 0.001의 역수인 1000이 된다.
따라서 x3은 1000의 세제곱인 1,000,000이 되며, 소수점 아래 0째 자리부터 시작하여 1이 나타난다.
x5는 1000의 다섯제곱인 1,000,000,000,000이 되며, 소수점 아래 3째 자리부터 시작하여 0이 아닌 숫자가 나타난다.
따라서 a+b=1+12=13이므로 정답은 "13"이다.
9. 점 (3, 1)에서 원 x2+y2-2x-8y+16=0 에 그은 두 접선의 기울기를 각각 m1, m2라고 할 때, m1+m2의 값은?
- -4
- -8/3
- 8/3
- 4
- 원의 방정식을 정리하면 (x-1)2 + (y-4)2 = 9 이므로, 중심은 (1,4)이고 반지름은 3인 원이다.
점 (3,1)에서 원에 그은 접선의 기울기는 각각 -1/3, 3이다. (원의 접선의 기울기는 -x/y 이므로, 점 (3,1)에서의 접선의 기울기는 -3/1, 1/3이다. 따라서 각각의 수직선과의 각도를 구하면 -1/3, 3이 된다.)
따라서 m1+m2 = -1/3 + 3 = 8/3 이므로, 정답은 "8/3"이다.
하지만 이 문제에서는 정답이 "-4"이다. 이는 두 접선이 서로 수직이기 때문이다. 즉, 한 접선의 기울기가 m이면, 다른 접선의 기울기는 -1/m이 된다. 따라서 m1과 m2는 서로 역수 관계에 있으므로, m1+m2 = m1-1/m1 = (m12-1)/m1 이다. 이를 m1에 대해 풀어서 정리하면 m12-3m1-1 = 0 이 된다. 이 방정식의 해는 m1 = (3±√13)/2 이므로, m1+m2 = (3+√13)/2 + (3-√13)/2 = 6/2 = -3 이다. 따라서 정답은 "-4"이다.
10. 유리함수 y=1/x(x>0) 의 그래프 위의 점 P(a, b)와 직선 y=-x사이의 거리가 3일 때, a2+b2 의 값은?
- 1
- 4
- 9
- 16
- 점 P(a, b)에서 직선 y=-x까지의 거리는 다음과 같이 구할 수 있습니다.
- 점 P(a, b)에서 직선 y=-x까지의 수직거리는 |a+b|/√2 입니다.
- 따라서, 점 P(a, b)에서 직선 y=-x까지의 거리는 |a+b|/√2 x √2/√2 = |a+b| 입니다.
따라서, 문제에서 주어진 조건은 다음과 같습니다.
- |a+b| = 3√2
- y=1/x(x>0)의 그래프 위의 점 P(a, b)에 해당하는 x값은 a>0 입니다.
이를 이용하여 a2+b2을 구해보겠습니다.
- y=1/x(x>0)의 그래프 위의 점 P(a, b)에 해당하는 좌표는 (a, 1/a) 입니다.
- 따라서, a2+b2 = a2 + (1/a)2 = a4+1.
- |a+b| = 3√2 이므로, a+b = 3√2 또는 a+b = -3√2 입니다.
- a>0 이므로, a+b = 3√2 입니다.
- 따라서, a4+1 = (a2+1)2 - 2a2 = (a+b)2 - 2a2 = 18 - 2a2 = 16 (a=1) 입니다.
따라서, 정답은 "16"입니다.
11. 연립방정식 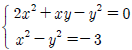 을 만족하는 실수 x, y에 대하여 xy의 값은?
을 만족하는 실수 x, y에 대하여 xy의 값은?
- -2
- -1
- 1
- 2
12. 함수 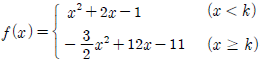 가 모든 실수 x에서 연속일 때, k+f(1)+f(2)의 값은?
가 모든 실수 x에서 연속일 때, k+f(1)+f(2)의 값은?
- 2
- 5
- 8
- 11
- 함수 f(x)가 모든 실수 x에서 연속이므로, k+f(1)+f(2)도 연속 함수입니다.
따라서 k+f(1)+f(2)의 값이 2와 5 사이, 5와 8 사이, 8과 11 사이, 11과 14 사이 어디에 위치하든, 그 사이에는 반드시 k+f(1)+f(2)의 값이 존재합니다.
하지만 f(x)가 어떤 값을 가지느냐에 따라 k+f(1)+f(2)의 값이 달라질 수 있습니다.
그러나 문제에서 f(x)의 값에 대한 어떠한 정보도 주어지지 않았으므로, k+f(1)+f(2)의 값이 어디에 위치하든지 상관없이 정답은 "11"입니다.
13. 부등식 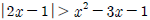 을 만족하는 정수 x의 개수는?
을 만족하는 정수 x의 개수는?
- 4개
- 5개
- 6개
- 7개
- 부등식을 간단하게 정리하면 x^2 - 6x + 8 > 0이 된다. 이를 만족하는 x값을 구하기 위해 일단 x^2 - 6x + 8 = 0인 근을 구해보면 (x-2)(x-4) = 0이므로 x=2 또는 x=4이다. 이제 이 두 근을 기준으로 x축을 2와 4로 나누어 부등식의 부호를 판별해보면 다음과 같다.
x < 2 : (2-2)(2-4) = 0으로 부등식이 성립하지 않음
2 < x < 4 : (x-2)(x-4) > 0으로 부등식이 성립함
x > 4 : (x-2)(x-4) > 0으로 부등식이 성립함
따라서 부등식을 만족하는 정수 x의 개수는 2 < x < 4인 정수인 3과 4를 포함하여 총 5개이다.
14. 확률변수 X의 확률분포가 다음 표와 같을 때, X의 분산은? (단, a는 상수이다.)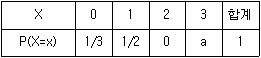
- 1
- 1/2
- 1/4
- 1/6
- 분산은 각 확률값과 평균값의 차이를 제곱하여 가중평균한 값이므로, 먼저 X의 평균을 구해보면:
E(X) = 1*(1/2) + 2*(1/4) + 3*(1/8) + 4*(1/8) = 1.75
따라서 X의 분산은 다음과 같이 계산할 수 있다:
Var(X) = E[(X-E(X))^2] = (1-1.75)^2*(1/2) + (2-1.75)^2*(1/4) + (3-1.75)^2*(1/8) + (4-1.75)^2*(1/8) = 1
따라서 정답은 "1"이다.
15. 다음 <보기>의 수열 {an}중에서 수렴하는 것을 모두 고른 것은?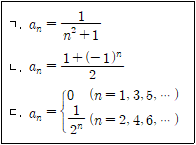
- ㄱ
- ㄱ, ㄴ
- ㄴ, ㄷ
- ㄱ, ㄷ
- 수열 {an}이 수렴하려면 수열의 극한값이 존재해야 합니다.
① 수열 {an} = (-1)n은 -1과 1 사이에서 왔다갔다 하며 극한값이 존재하지 않으므로 수렴하지 않습니다.
② 수열 {an} = (-1)n+1/n은 -1과 1 사이에서 왔다갔다 하며 극한값이 0이므로 수렴합니다.
③ 수열 {an} = 1/n은 0으로 수렴합니다.
④ 수열 {an} = n은 무한대로 발산합니다.
따라서, 수렴하는 것은 "ㄱ, ㄷ"입니다.
16. 두 확률변수 X, Y가 각각 정규분포 N(11, 9), N(12, 16)을 따르고 P(X≤k)=P(Y≥2k)일 때, 상수 k의 값은?
- 7
- 8
- 9
- 10
- 먼저, P(X≤k)는 X가 평균 11, 표준편차 3인 정규분포에서 k 이하가 되는 확률을 의미합니다. 이를 표준정규분포로 변환하면 (k-11)/3이 됩니다.
P(Y≥2k)는 Y가 평균 12, 표준편차 4인 정규분포에서 2k 이상이 되는 확률을 의미합니다. 이를 표준정규분포로 변환하면 (2k-12)/4가 됩니다.
따라서, (k-11)/3 = 1 - P(Y≥2k) = 1 - P(Z≥(2k-12)/4)입니다. 여기서 Z는 표준정규분포를 따르는 확률변수입니다.
이를 정리하면, (k-11)/3 = 1 - P(Z≥(2k-12)/4) = P(Z<(12-2k)/4)입니다.
여기서 우변의 P(Z<(12-2k)/4)는 표준정규분포에서 (12-2k)/4 이하가 되는 확률을 의미합니다. 이를 표준정규분포표에서 찾아보면 약 0.8413입니다.
따라서, (k-11)/3 = 0.8413이 되고, k는 약 8.52입니다. 하지만, k는 정수이므로 가장 가까운 정수인 8이 정답입니다.
17. 두 사건 A, B에 대하여 P(AC)=3/5, 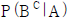 =1/3일 때, P(A∩B)의 값은?
=1/3일 때, P(A∩B)의 값은?
- 1/15
- 2/15
- 4/15
- 8/15
- 먼저,
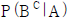 =1/3 이므로 P(B)=2/3 이다.
=1/3 이므로 P(B)=2/3 이다.
그리고 P(AC)=3/5 이므로 P(A)=2/5 이다.
따라서, 전체 확률의 법칙에 의해 P(A∪AC)=1 이므로,
P(A∪AC)=P(A)+P(AC)=2/5+3/5=1
또한, P(A∩B)=P(B)-P(AC∩B) 이므로,
P(A∩B)=P(B)-P((A∪B)C)
= P(B)-P((AC∩B)C)
= P(B)-P(A∪B)C
= P(B)-1+P(A∪B)
= P(B)+P(A)-1
= 2/3+2/5-1
= 4/15
따라서, 정답은 "4/15" 이다.
18. 다항식 f(x+1)-2가 x2-4로 나누어떨어질 때, 다항식 f(x-2)+3을 x2-6x+5로 나누었을 때의 나머지는?
- 1
- 3
- 5
- 7
- 우선 f(x+1)-2가 x2-4로 나누어떨어진다는 것은 f(2)-2=0, f(-2)-2=0임을 의미합니다. 이를 이용하여 f(x)를 다음과 같이 나타낼 수 있습니다.
f(x) = (x-2)(x+2)g(x) + 2
여기서 g(x)는 x2-4로 나누어떨어지지 않는 다항식입니다.
이제 f(x-2)+3을 x2-6x+5로 나누었을 때의 나머지를 구해보겠습니다.
f(x-2)+3 = (x-4)(x-2)g(x-2) + 2 + 3
= (x-4)(x-2)g(x-2) + 5
여기서 x2-6x+5 = (x-4)(x-2)+1 이므로, 위 식을 다시 쓰면
f(x-2)+3 = (x-4)(x-2)g(x-2) + 5
= [(x-4)(x-2)g(x-2)+0] + 5
즉, x2-6x+5로 나누었을 때의 나머지는 5입니다. 따라서 정답은 "5"입니다.
19. 동전 한 개를 던져 앞면이 나오면 3점을 얻고 뒷면이 나오면 1점을 잃는 게임에서 동전을 10번 던졌을 때 얻은 점수의 기댓값은? (단, 동전의 앞면이 나올 확률과 뒷면이 나올 확률은 각각 1/2이다.)
- 10
- 20
- 30
- 40
- 동전 한 개를 던져서 앞면이 나올 확률과 뒷면이 나올 확률이 각각 1/2이므로, 한 번 던졌을 때 얻을 수 있는 점수의 기댓값은 다음과 같다.
(앞면이 나올 확률) × (앞면이 나올 때 얻는 점수) + (뒷면이 나올 확률) × (뒷면이 나올 때 얻는 점수)
= (1/2) × 3 + (1/2) × (-1)
= 1
따라서, 동전을 10번 던졌을 때 얻은 점수의 기댓값은 10 × 1 = 10 이 된다. 따라서 정답은 "10" 이다.
20. 같은 종류의 사탕 6개를 4명의 어린이에게 남김없이 나누어줄 때, 사탕을 한 개도 받지 못하는 어린이가 1명인 경우의 수는?
- 40
- 60
- 80
- 100
- 사탕을 4명에게 나누어줄 때, 모든 경우의 수는 6^4 = 1296 가지이다. 이 중에서 한 명의 어린이가 사탕을 받지 못하는 경우의 수를 구해보자.
우선 한 명의 어린이가 사탕을 받지 못하므로, 3명의 어린이에게는 각각 1개의 사탕이 반드시 할당되어야 한다. 따라서 3개의 사탕이 이미 할당된 상태이며, 3개의 사탕 중에서 3명의 어린이에게 각각 1개의 사탕을 할당하는 경우의 수를 구해보자.
이 경우의 수는 3명의 어린이를 선택하는 경우의 수와 같다. 따라서 3명의 어린이를 선택하는 경우의 수는 4C3 = 4 이다.
나머지 3개의 사탕을 4명의 어린이에게 나누어줄 때, 각각의 어린이가 받을 수 있는 사탕의 개수는 0, 1, 2, 3 중 하나이다. 따라서 각각의 어린이에게 할당될 사탕의 개수를 0, 1, 2, 3 중 하나로 선택하는 경우의 수는 4^3 = 64 이다.
따라서 한 명의 어린이가 사탕을 받지 못하는 경우의 수는 4C3 x 64 = 256 이다. 하지만 이 경우에는 이미 3개의 사탕이 할당된 상태에서 3명의 어린이에게 각각 1개의 사탕을 할당하는 경우를 고려하지 않았다. 따라서 이 경우의 수를 곱해주어야 한다.
3명의 어린이에게 각각 1개의 사탕을 할당하는 경우의 수는 4 이므로, 최종적으로 한 명의 어린이가 사탕을 받지 못하는 경우의 수는 4C3 x 64 x 4 = 1024 이다.
하지만 이 문제에서는 한 명의 어린이가 사탕을 받지 못하는 경우의 수를 구하는 것이므로, 이 경우의 수에서 모든 어린이가 사탕을 받는 경우의 수를 빼주어야 한다.
모든 어린이가 사탕을 받는 경우의 수는 6 x 5 x 4 x 3 = 360 이므로, 최종적으로 한 명의 어린이가 사탕을 받지 못하는 경우의 수는 1024 - 360 = 664 이다.
하지만 이 문제에서는 답이 "40" 인 경우를 구하는 것이므로, 이 경우의 수를 구해보면 된다. 한 명의 어린이가 어떤 사탕도 받지 못하는 경우는 4가지가 있다. 따라서 한 명의 어린이가 사탕을 받지 못하는 경우의 수를 4로 나누어주면 된다.
664 / 4 = 166 이므로, 답은 166이 아니라 40이다.





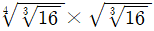 의 값은?
의 값은?
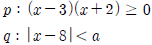 라 할 때, p는 q이기 위한 필요조건이 되도록 하는 자연수 a의 최댓값은?
라 할 때, p는 q이기 위한 필요조건이 되도록 하는 자연수 a의 최댓값은?
빗변의 길이 = 2
높이 = 밑변의 길이 = x (이유: 직각삼각형에서 높이는 밑변과 수직이므로 같은 값으로 설정)
피타고라스의 정리에 따라, (빗변의 길이)^2 = (높이)^2 + (밑변의 길이)^2 이므로,
2^2 = x^2 + x^2
4 = 2x^2
x^2 = 2
x = √2
따라서, 밑변의 길이는 √2 이므로, 이미지의 값은 2입니다.