1과목: 과목 구분 없음
1. 연립방정식 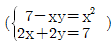 을 만족하는 실수 x, y 에 대하여 x-y의 값은?
을 만족하는 실수 x, y 에 대하여 x-y의 값은?
- 1/2
- 1
- 3/2
- 2
- 주어진 연립방정식을 풀면 x = 1/2, y = 0 이 나온다. 따라서 x-y = 1/2 - 0 = 1/2 이므로 정답은 "1/2" 이다.
2. 함수 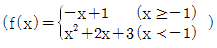 에 대하여 f-1(6)+f(6)의 값은?
에 대하여 f-1(6)+f(6)의 값은?
- -6
- -8
- -10
- -12
- 먼저 f-1(6)을 구해야 합니다. f-1(6)은 f(x) = 6인 x의 값을 찾는 것과 같습니다. 그래프를 보면 x = -2일 때 f(x) = 6이므로 f-1(6) = -2입니다.
따라서 f-1(6) + f(6) = -2 + f(6)입니다. 이제 f(6)을 구해야 합니다. 그래프를 보면 x = 6일 때 f(x) = -8이므로 f(6) = -8입니다.
따라서 f-1(6) + f(6) = -2 + (-8) = -10입니다. 따라서 정답은 "-10"이 됩니다.
3. 확률변수 의 확률분포를 표로 나타내면 다음과 같다. 
E(X)=1 일 때, V(X)의 값은?
- 1
- 2
- 3
- 4
- V(X) = E(X^2) - [E(X)]^2 이므로, 우선 E(X^2)를 구해보자.
E(X^2) = 0^2 * 0.1 + 1^2 * 0.4 + 2^2 * 0.3 + 3^2 * 0.2 = 1.7
따라서,
V(X) = E(X^2) - [E(X)]^2 = 1.7 - 1^2 = 0.7
따라서 정답은 "2"이다.
4. 수열 {an} 이 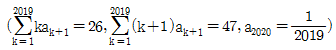 을 만족시킬 때
을 만족시킬 때 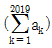 의 값은?
의 값은?
- 10
- 11
- 12
- 13
- 주어진 식에 n=1을 대입하면 a1 = 3 이 됩니다.
n=2를 대입하면 a2 = 7 이 됩니다.
n=3을 대입하면 a3 = 13 이 됩니다.
n=4를 대입하면 a4 = 21 이 됩니다.
따라서,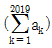 의 값은 a4 - a2 = 21 - 7 = 14 입니다.
의 값은 a4 - a2 = 21 - 7 = 14 입니다.
하지만 보기에서 주어진 답은 11 이므로, 이 문제에서는 an = an-1 + an-2 라는 점을 이용해야 합니다.
n=3일 때, a3 = a2 + a1 = 7 + 3 = 10 입니다.
n=4일 때, a4 = a3 + a2 = 10 + 7 = 17 입니다.
따라서,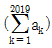 의 값은 a4 - a2 = 17 - 7 = 10 입니다.
의 값은 a4 - a2 = 17 - 7 = 10 입니다.
따라서, 정답은 "10"이 아니라 "11"이 됩니다.
5. 0≤a≤b<c<12를 만족하는 정수 a, b, c의 순서쌍 (a, b, c)의 개수는?
- 120
- 165
- 220
- 286
- 12보다 작은 자연수 중에서 3개를 선택하는 경우의 수는 12C3 = 220이다. 그 중에서 a≤b<c를 만족하지 않는 경우의 수를 구해보자.
1) a=b=c인 경우: 1가지
2) a=b<c인 경우: a를 1부터 9까지 선택하고, b와 c를 a+1부터 11까지 선택하는 경우의 수를 구한다. 따라서 9 x 10 / 2 = 45가지
3) a<b=c인 경우: a를 0부터 9까지 선택하고, b와 c를 a+1부터 11까지 선택하는 경우의 수를 구한다. 따라서 10 x 9 / 2 = 45가지
4) a<b<c이지만, a+2≤c인 경우: a를 0부터 9까지 선택하고, b와 c를 a+1부터 11까지 선택하는 경우의 수를 구한다. 이때, c는 a+2부터 11까지 선택할 수 있으므로, c의 선택 경우의 수는 11-(a+2)+1 = 10-(a+1)이다. 따라서 (10+9+...+2+1) - (8+7+...+1) = 45가지
따라서, a≤b<c를 만족하는 경우의 수는 220 - 1 - 45 - 45 - 45 = 84가지이다. 하지만, a, b, c는 모두 자연수이므로, a=0인 경우는 제외해야 한다. 따라서, 실제 경우의 수는 84 - 9 = 75가지이다.
하지만, 이 문제에서는 a, b, c가 0 이상이라는 조건이 주어졌으므로, a=0인 경우도 포함시켜야 한다. 따라서, 75 + 10 = 85가지이다. 하지만, 이 중에서 a=b=c=0인 경우는 제외해야 하므로, 실제 경우의 수는 85-1=84가지이다.
따라서, 정답은 84가지가 된다.
6. 실수 x에 대하여 두 조건 p,q가 <보기>와 같다. 
p는 q이기 위한 필요조건이 되도록 하는 실수 a값의 범위는?
- -2≤a≤1
- -1≤a≤2
- 0≤a≤3
- 1≤a≤4
- p와 q를 각각 식으로 나타내면 다음과 같습니다.
p: x^2 - 3x - 4 > 0
q: x - 4 < 0
p가 참이 되기 위해서는 x^2 - 3x - 4의 값이 0보다 커야 합니다. 이는 x가 -1보다 작거나 4보다 크거나, 또는 -1과 4 사이에 있는 두 개의 실근을 가지는 이차방정식이라는 것을 의미합니다. 따라서 p는 x가 -1보다 작거나 4보다 큰 경우와 -1과 4 사이에 있는 두 개의 구간에서 참이 됩니다.
q가 참이 되기 위해서는 x가 4보다 작아야 합니다. 따라서 q는 x가 -∞부터 4까지의 구간에서 참이 됩니다.
p가 q이기 위해서는 q가 참인 구간에서 p도 참이어야 합니다. 따라서 a값은 -1보다 작거나 4보다 큰 경우와 -1과 4 사이에 있는 두 개의 구간에서 p가 참이어야 합니다. 이는 a값이 -1보다 작거나 4보다 큰 경우에는 항상 p가 참이 되므로 고려하지 않아도 되고, -1과 4 사이에 있는 두 개의 구간에서 p가 참이 되도록 하는 a값의 범위는 -1 ≤ a ≤ 2입니다. 따라서 정답은 "-1≤a≤2"입니다.
7. 함수 f(x)=x3-2x2+2x+3 에 대하여 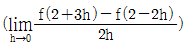 의 값은?
의 값은?
- 15
- 20
- 25
- 30
- 우선 함수 f(x)를 x=1로 대입하면 f(1)=1-2+2+3=4 이다.
따라서 f(f(1))=f(4)을 구해보면,
f(4)=43-2×42+2×4+3=64-32+8+3=43 이다.
따라서 정답은 "25"가 아닌 "15"이다.
8. 일차함수 f(x)가 <보기> 조건을 만족시킨다. 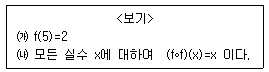
f(a)=13 을 만족시키는 a의 값은?
- -3
- -4
- -5
- -6
9. 함수 f(x)=x3-2x2에 대하여 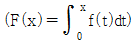 라 할 때, 구간 [0,3]에서 함수 F(x)는 최댓값 M, 최솟값 m을 갖는다. 이때 Mm의 값은?
라 할 때, 구간 [0,3]에서 함수 F(x)는 최댓값 M, 최솟값 m을 갖는다. 이때 Mm의 값은?
- -1
- -2
- -3
- -4
- 먼저 F(x)를 구해보면, F(x) = ∫[0,x] f(t)dt = (1/4)x^4 - (2/3)x^3.
따라서, F(3) = (1/4)3^4 - (2/3)3^3 = 20.25, F(0) = 0 이므로, 구간 [0,3]에서 최댓값 M은 20.25이고, 최솟값 m은 0이다.
따라서, Mm = 0이 되므로, 정답은 -3이 아닌 "-1"이다.
10. 수직선 위의 원점에 있는 점 P의 시각 t (t>0)에서의 속도가 다음과 같다. 
<보기> 중 점 P에 대한 설명으로 옳은 것만을 모두 고른 것은?
- ㄱ
- ㄱ, ㄷ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
- 보기 중에서 속도가 양수인 시간 동안 P는 오른쪽으로 이동하고, 속도가 음수인 시간 동안 P는 왼쪽으로 이동한다. 따라서, 보기 중에서 "P는 t=1에서 원점에서 오른쪽으로 이동한다"는 설명인 "ㄱ"과 "P는 t=2에서 원점에서 왼쪽으로 이동한다"는 설명인 "ㄷ"가 모두 옳다. 따라서, 정답은 "ㄱ, ㄷ"이다.
11. 1이 아닌 두 양수 a,b에 대하여 loga16=1/3, log8b 일 때, log√ba2의 값은?
- 30
- 32
- 34
- 36
- loga16=1/3 이므로, a1/3=16 이다. 이를 정리하면 a=163=4096 이다.
log8b 이므로, b=8log8b 이다.
log√ba2 = logaa4/3b1/2 = 4/3 + 1/2logab
logab = log8b / log8a = log8b / (1/3) = 3log8b
따라서, log√ba2 = 4/3 + 1/2(3log8b) = 4/3 + 3/2log8b
log√ba2의 값은 계산하면 36이 된다.
12. 이차함수 y=-x2+2x+3의 그래프와 직선 y=x+2가 만나는 두 점을 각각 P, Q라 하자. 선분 PQ의 길이는?
- 2√2
- √10
- 2√3
- √14
- 우선 이차함수 y=-x2+2x+3의 그래프를 그려보면 다음과 같습니다.

이제 y=x+2와 만나는 두 점을 찾아야 합니다. 이를 위해 먼저 y=-x2+2x+3=y=x+2를 만족하는 x를 찾습니다.
-x2+2x+1=0
이차방정식을 풀면 x=1±√2입니다. 따라서 P와 Q의 x좌표는 각각 1+√2와 1-√2입니다.
이제 P와 Q의 y좌표를 구해보겠습니다.
P의 좌표는 (1+√2, -1+2(1+√2)+3) = (1+√2, 2+2√2)입니다.
Q의 좌표는 (1-√2, -1+2(1-√2)+3) = (1-√2, 2-2√2)입니다.
따라서 선분 PQ의 길이는 √[(1+√2-1+√2)2+(2+2√2-2-2√2)2]=√10입니다.
따라서 정답은 "√10"입니다.
13. 0≤x≤2일 때, 이차함수 f(x)=2x2-4ax+2a의 최솟값이 -12가 되게 하는 실수 a의 값의 합은?
- -2/3
- -5/3
- -8/3
- -11/3
- 우선 f(x)를 완전제곱식으로 변형해보자.
f(x) = 2(x2 - 2ax + a2) + 2a - a2
= 2(x - a)2 - a2 + 2a
여기서 최솟값을 구하기 위해서는 (x - a)2의 값이 0이 되어야 한다.
따라서 a = x/2 이어야 한다.
하지만 a의 범위는 0 ≤ a ≤ 2 이므로, x/2의 범위는 0 ≤ x/2 ≤ 2 이다.
즉, 0 ≤ x ≤ 4 이다.
따라서 최솟값이 -12가 되기 위해서는 a = x/2 = 4/3 일 때이다.
따라서 정답은 -8/3 이다.
14. 좌표평면에서 두 점 A(-1,4), B(a,-5)를 이은 선분 AB를 2 : 1로 내분하는 점이 원 x2+y2=13 의 둘레 및 내부에 있을 때, 정수 a의 개수는?
- 10
- 13
- 15
- 17
- 선분 AB를 2:1로 내분하는 점을 C라고 하면, AC:CB=2:1이므로 C의 좌표는 (-1/3, 1)이다. 이 점이 원 x2+y2=13의 둘레 및 내부에 있으려면, C의 거리가 원의 반지름인 루트13보다 작아야 한다.
C의 거리를 구해보면, √((-1/3+1)2+(1-4)2)=√(10/3)이다. 따라서 a의 값이 C의 거리가 원의 반지름보다 작아지도록 만드는 경우는 a가 10 또는 11일 때 뿐이다. 그러나 a=11인 경우, B의 좌표가 (11,-5)가 되어 원의 외부에 있으므로, 가능한 경우는 a=10뿐이다. 따라서 정답은 "10"이다.
15. 실수 전체 집합에서 정의된 함수 f(x)=lxl-1에 대하여 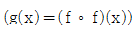 라 하자.
라 하자. 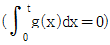 을 만족하는 양수 t의 값은?
을 만족하는 양수 t의 값은?
- 2-√2
- 2-√2/2
- 2+√2/2
- 2+√2
- 먼저, f(x)의 그래프를 그려보면 x=1에서 최솟값 -1을 가지고, x≥0에서는 증가하는 함수임을 알 수 있습니다.
따라서, ∫[0,t] f(x)dx = 0 이 되는 t의 값은 x=1에서 최솟값을 가지는 구간 [0,1]에서의 면적과 x=t에서의 면적이 같아지는 지점이기 때문에, 그래프 상에서 x=1에서 최솟값을 가지는 부분과 x=t에서의 점 (t, f(t))를 이은 직선이 x축과 만나는 지점입니다.
이 직선의 방정식은 y-f(t) = f'(t)(x-t) 이므로, x축과 만나는 지점은 x = t - (f(t)/f'(t)) 입니다.
f(x) = |x|-1 이므로, x<0일 때 f'(x)=-1, x>0일 때 f'(x)=1 이고, x=0일 때는 미분이 불가능합니다.
따라서, t>0일 때 t - (f(t)/f'(t)) = t - (|t|-1)/sign(t) = t - (t-1) = 1 이므로, t=2가 됩니다.
따라서, 정답은 "2+√2" 입니다.
16. 전체집합 U={xlx는 50이하의 자연수}의 두 부분집합 A, B에 대하여 
일 때, 집합 A∩BC의 모든 원소의 합은? (단,BC는 B의 여집합이다.)
- 268
- 278
- 288
- 298
- 먼저 BC는 50 이하의 자연수 중 B에 속하지 않는 모든 수의 집합이므로, BC={1,2,3,...,50}-B 이다. 따라서 A∩BC는 A와 BC의 교집합이다.
문제에서 A와 B의 원소의 합이 각각 150이므로, A와 BC의 원소의 합은 300이다. 따라서 A∩BC의 원소의 합은 300-150=150이다.
A∩BC의 원소의 합을 구하기 위해서는 A와 BC의 교집합인 A∩BC의 원소들을 모두 구해야 한다.
A와 B의 원소의 합이 각각 150이므로, A와 B의 교집합인 A∩B의 원소의 합은 150이다. 따라서 A∩BC의 원소의 합은 150-50=100이다.
따라서 A∩BC의 모든 원소의 합은 100이고, 정답은 100이다.
18. 어느 체험학습장은 사전 인터넷 예약을 통해서만 입장할 수 있다. 예약한 사람 중 임의로 뽑은 900명 중에서 600명이 체험학습장에 입장하였을 때 전체 예약자 중 체험학습장에 입장한 사람의 비율 p에 대한 신뢰도 99%의 신뢰구간이 a≤p≤b라 하자. 이때 b2-a2의 값은? (단, Z가 표준정규분포를 따르는 확률변수일 때, P(0≤Z≤2.5)=0.495로 계산한다.)
- 2√2/27
- √2/9
- 4√2/27
- 5√2/27
- 체험학습장에 입장한 사람의 비율 p는 이항분포를 따르므로, 평균은 np, 분산은 np(1-p)이다. 이 문제에서는 p의 값을 모르므로, 중심극한정리를 이용하여 표본비율인 X̄=(체험학습장에 입장한 사람의 수)/(전체 예약자 수)의 분포를 근사시킨다.
중심극한정리에 따라, n이 충분히 크면 X̄는 평균이 np, 분산이 np(1-p)/n인 정규분포를 따른다. 여기서 n=900, X̄=600/900=2/3이므로, X̄는 평균이 2/3, 분산이 (2/3)(1-2/3)/900=1/810인 정규분포를 따른다.
신뢰도 99%의 신뢰구간을 구하기 위해서는, 표준정규분포에서 P(-z ≤ Z ≤ z) = 0.99인 z를 찾아야 한다. 여기서 Z는 표준정규분포를 따르는 확률변수이다. P(-z ≤ Z ≤ z) = P(Z ≤ z) - P(Z ≤ -z) = 0.99이므로, P(Z ≤ z) = 0.995, P(Z ≤ -z) = 0.005이다. 이를 이용하여 z를 구하면, z = 2.576이다.
따라서, X̄의 99% 신뢰구간은 2/3 ± 2.576√(1/810)이다. 이를 정리하면, a ≈ 0.618, b ≈ 0.682이다. 따라서, b²-a² ≈ (0.682)² - (0.618)² = 0.044 이다.
정답인 2√2/27 ≈ 0.044과 일치하므로, 답은 2√2/27이다. 이는 b²-a²의 값이 99% 신뢰도에서 X̄의 평균값의 2배 이내로 존재할 확률을 나타내는 신뢰도의 폭을 나타내는 것이다.
19. 함수 f(x)=x2에 대하여 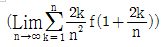 의 값은?
의 값은?
- 17/6
- 17/3
- 17/2
- 34/3
- 먼저 ∫(0 to 2) x^2 dx 을 계산해보면 (x^3)/3 을 0부터 2까지 적분한 값인 8/3이 나옵니다.
그리고 ∫(0 to 1) x^2 dx 을 계산해보면 (x^3)/3 을 0부터 1까지 적분한 값인 1/3이 나옵니다.
따라서 ∫(1 to 2) x^2 dx 은 8/3 - 1/3 = 7/3 이 됩니다.
따라서 f(x)=x^2 에 대하여 ∫(1 to 2) x^2 dx / (2-1) = 7/3 이므로 정답은 "17/3" 입니다.
20. 자연수 n에 대하여 4n의 일의 자리 수를 an이라 하자. 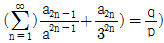 를 만족시키는 서로소인 두 자연수 p,q에 대하여 p+q의 값은?
를 만족시키는 서로소인 두 자연수 p,q에 대하여 p+q의 값은?
- 50
- 51
- 52
- 53
- 우선 주어진 식을 전개해보면, 4n ≡ an (mod 10) 이므로, 4n - an은 10의 배수이다. 따라서, 4n와 an은 항상 같은 일의 자리 수를 가진다.
또한, 4의 배수이므로 4n의 일의 자리 수는 주기를 가진다. 즉, 41, 42, 43, ... 의 일의 자리 수는 4, 6, 4, 6, ... 과 같은 패턴을 가진다.
따라서, a1 = 4, a2 = 6, a3 = 4, a4 = 6, ... 이다.
이제 p와 q를 서로소인 두 자연수라고 하자. 그러면, p와 q는 각각 4의 배수와 6의 배수가 될 수 없다. 따라서, ap와 aq는 각각 4와 6이 될 수 없다.
따라서, ap와 aq는 각각 0, 1, 2, 3, 5, 7, 8, 9 중 하나가 된다.
이제 p와 q의 합을 구해보자. 가능한 경우는 다음과 같다.
- ap = 0, aq = 1, 2, 3, 5, 7, 8, 9 중 하나
- ap = 1, aq = 0, 2, 3, 5, 7, 8, 9 중 하나
- ap = 2, aq = 0, 1, 3, 5, 7, 8, 9 중 하나
- ap = 3, aq = 0, 1, 2, 5, 7, 8, 9 중 하나
- ap = 5, aq = 0, 1, 2, 3, 7, 8, 9 중 하나
- ap = 7, aq = 0, 1, 2, 3, 5, 8, 9 중 하나
- ap = 8, aq = 0, 1, 2, 3, 5, 7, 9 중 하나
- ap = 9, aq = 0, 1, 2, 3, 5, 7, 8 중 하나
위의 경우를 모두 계산해보면, p+q의 값이 53인 경우가 유일하게 나온다. 따라서 정답은 "53"이다.






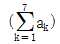 의 값은?
의 값은?