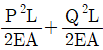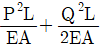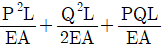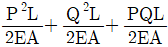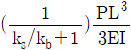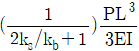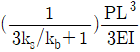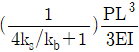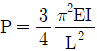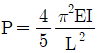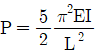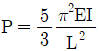1과목: 과목 구분 없음
1. 구조물의 처짐을 구하는 방법 중 공액보법에 대한 다음 설명으로 가장 옳지 않은 것은?
- 지지조건이 이동단인 경우 공액보는 자유단으로 바꾸어 계산한다.
- M/EI(곡률)을 공액보에 하중으로 작용시켜 계산한다.
- 공액보의 최대전단력 발생 지점에서 최대처짐각을 계산한다.
- 공액보의 전단력이 0인 지점에서 최대처짐을 계산한다.
2. 그림과 같은 축력 P, Q를 받는 부재의 변형에너지는? (단, 보의 축강성은 EA로 일정하다.)
3. 그림과 같이 캔틸레버보에 하중이 작용하고 있다. 동일한 재료 및 단면적을 가진 두 구조물의 자유단 A에서 동일한 처짐이 발생하기 위한 P와 w관계로 옳은 것은?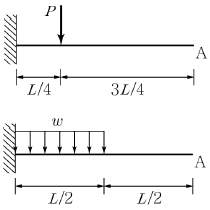
- P= 7wL / 10
- P= 7wL / 11
- P= 7wL / 12
- P= 7wL / 13
4. 사각형 단면으로 설계된 보가 분포하중과 집중하중을 받고 있다. 그림과 같이 단면의 높이는 같으나 단면 폭은 구간 AB가 구간 BC에 비해 1.5배 크다. 이 경우 구간 AB와 구간 BC에서 발생하는 최대휨응력의 비( 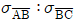 )는?
)는?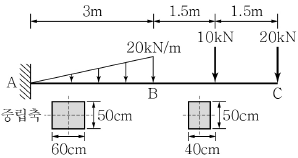
- 1 : 1.5
- 1.5 : 1
- 1 : 2
- 2 : 1
5. 그림과 같은 3힌지 라멘에서 A점의 수직반력 VA 및 B점의 수평반력 HB로 옳은 것은?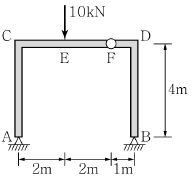
- VA=6kN(↑), HB=1kN(←)
- VA=4kN(↑), HB=1kN(←)
- VA=6kN(↑), HB=1kN(→)
- VA=4kN(↑), HB=1kN(→)
6. 그림과 같은 단면의 도심의 좌표는?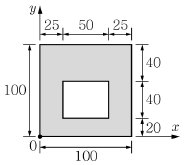
- (50, 47.5)
- (50, 50.0)
- (50, 52.5)
- (50, 55.0)
7. 그림과 같이 100N의 전단강도를 갖는 못(nail)이 웨브(web)와 플랜지(flange)를 연결하고 있다. 이 못들은 부재의 길이방향으로 150mm 간격으로 설치되어 있다. 이 부재에 작용할 수 있는 최대수직전단력은? (단, 단면2차모멘트 I=1,012,500mm4)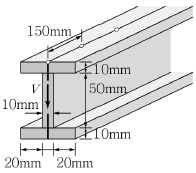
- 35N
- 40N
- 45N
- 50N
8. 그림과 같은 직사각형 단면을 갖는 보가 집중하중을 받고 있다. 보의 길이 L이 5m일 경우 단면 a-a의 c 위치에서 발생하는 주응력(σ1, σ2)은? (단, (+) : 인장, (-) : 압축)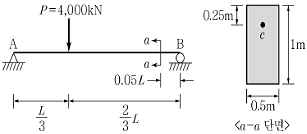
- (2+√10, 2-√10)
- (-2+√10, -2-√10)
- (1+√10, 1-√10)
- (-1+√10, -1-√10)
9. 그림과 같이 단면적이 200mm2인 강봉의 양단부(A점 및 B점)를 6월(25℃)에 용접하였을 때, 다음 해 1월(-5℃)에 AB부재에 생기는 힘의 종류와 크기는? (단, 강봉의 탄성계수 E=2.0×105MPa, 열팽창계수 α=1.0×10-5/℃이고, 용접부의 온도변형은 없는 것으로 가정한다.)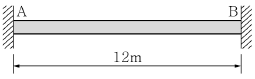
- 인장력 8kN
- 인장력 12kN
- 압축력 8kN
- 압축력 12kN
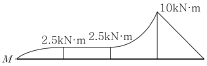
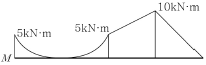
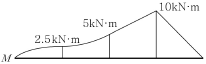
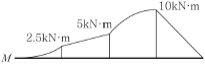
10. 아래 그림은 어느 단순보의 전단력도이다. 이 보의 휨모멘트도는? (단, 이 보에 집중모멘트는 작용하지 않는다.)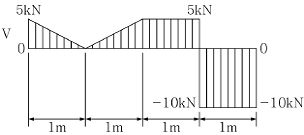
11. 그림과 같이 지점조건이 다른 3개의 기둥이 단면중심에 축하중을 받고 있다. 좌굴하중이 큰 순서대로 나열된 것은?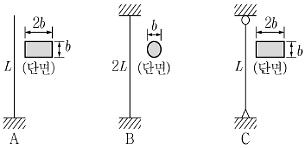
- B, A, C
- B, C, A
- C, A, B
- C, B, A
12. 그림과 같은 단면으로 설계된 보가 집중하중과 등분포하중을 받고 있다. 보의 허용휨응력이 42MPa일 때 보에 요구되는 최소 단면으로 적합한 a값은?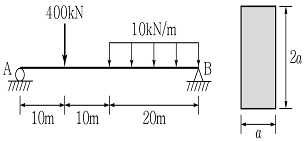
- 0.40m
- 0.50m
- 0.60m
- 0.70m
13. 그림과 같이 일정한 두께 t=10mm의 원형 단면을 갖는 튜브가 비틀림모멘트 T=40kN⋅m를 받을 때 발생하는 전단흐름의 크기(kN/m)는?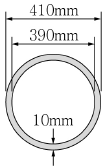
- 500/π
- 400/π
- π/350
- π/300
14. 그림과 같이 상하부에 알루미늄판과 내부에 플라스틱 코어가 있는 샌드위치 패널에 휨모멘트 4.28N⋅m가 작용하고 있다. 알루미늄판은 두께 2mm, 탄성계수는 30GPa이고 내부 플라스틱 코어는 높이 6mm, 탄성계수는 10GPa이다. 부재가 일체거동한다고 가정할 때 외부 알루미늄판의 최대응력은?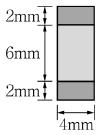
- 25N/mm2
- 30N/mm2
- 60N/mm2
- 75N/mm2
15. 그림과 같은 T형 단면에 수직방향의 전단력 V가 작용하고 있다. 이 단면에서 최대전단응력이 발생하는 위치는 어디인가? (단, c는 도심까지의 거리)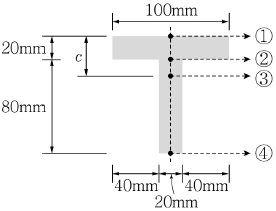
- ①
- ②
- ③
- ④
16. 휨강성이 EI로 일정한 캔틸레버보가 그림과 같이 스프링과 연결되어있다. 이 구조물이 B점에서 하중 P를 받을 때 B점에서의 변위는? (단, ks는 스프링 상수이며 보의 강성 kb=3EI/L3 이다.)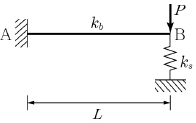
17. 그림의 수평부재 AB의 A지점은 힌지로 지지되고 B점에는 집중 하중 P가 작용하고 있다. C점과 D점에서는 끝단이 힌지로 지지된 길이가 L이고 휨강성이 모두 EI로 일정한 기둥으로 지지되고 있다. 두 기둥 모두 좌굴에 의해서 붕괴되는 하중 P의 크기는? (단, AB부재는 강체이다.)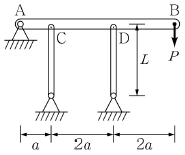
18. 그림과 같이 단면적이 1.5A, A, 0.5A인 세 개의 부재가 연결된 강체는 집중하중 P를 받고 있다. 이때 강체의 변위는? (단, 모든 부재의 탄성계수는 E로 같다.)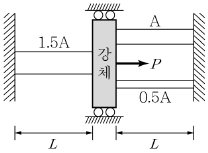
- PL / 1.5EA
- PL / 2.0EA
- PL / 2.5EA
- PL / 3.0EA
19. 그림과 같은 구조물에서 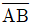 의 부재력과
의 부재력과 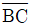 의 부재력은? (단, 모든 절점은 힌지임)
의 부재력은? (단, 모든 절점은 힌지임)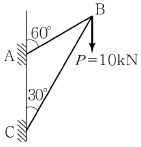
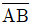 =10kN (인장),
=10kN (인장), 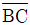 =10√3kN (압축)
=10√3kN (압축)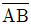 =10kN (압축),
=10kN (압축), 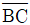 =10√3kN (인장)
=10√3kN (인장)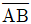 =10√3kN (인장),
=10√3kN (인장), 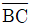 =10kN (압축)
=10kN (압축)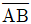 =10√3kN (압축),
=10√3kN (압축), 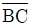 =10kN (인장)
=10kN (인장)
20. 그림과 같이 양단이 고정된 원형부재에 토크(Torque) T=400N⋅m가 A단으로부터 0.4m 떨어진 위치에 작용하고 있다. 단면의 지름이 40mm일 때 토크 T가 작용하는 단면에서 발생하는 최대전단응력의 크기와 비틀림각은? (단, GJ는 비틀림 강도)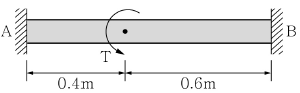
- 40/π MPa, 96/GJ rad
- 40/π MPa, 160/GJ rad
- 60/π MPa, 96/GJ rad
- 60/π MPa, 160/GJ rad