1과목: 과목 구분 없음
1. <보기>와 같이 동력차가 강성도 k=2TN/m인 스프링으로 구성된 차막이에 100m/s의 속도로 충돌할 때 스프링의 최대 수평 변위량은? (단, 동력차의 무게는 80tf이다.)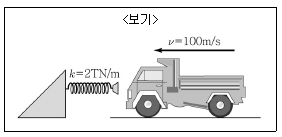
- 0.01m
- 0.015m
- 0.02m
- 0.025m
2. <보기>와 같이 주어진 문제의 반력으로 가장 옳은 것은?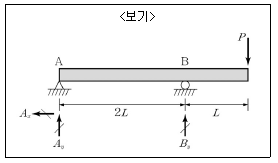
- Ax=0, Ay=0.5P, By=0.5P
- Ax=0, Ay=-0.25P, By==1.75P
- Ax=0, Ay=-0.5P, By=1.5P
- Ax=P, Ay=0.5P, By=1.5P
3. <보기>와 같은 구조물의 부정정 차수는?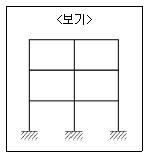
- 15
- 16
- 17
- 18
4. <보기>와 같은 직사각형 단면의 E점에 하중(P)이 작용할 경우 각 모서리 A, B, C, D의 응력은? (단, 압축은 +이고, 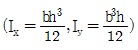 이다.)
이다.)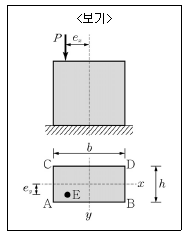
5. <보기>와 같은 트러스에서 단면법으로 구한 U의 부재력의 크기는?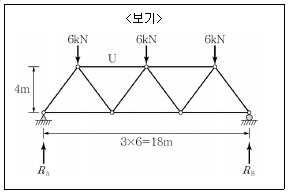
- 9kN
- 11kN
- 13kN
- 15kN
6. <보기>와 같이 모멘트하중을 받는 내민보가 있을 때 C점의 처짐각 θc와 처짐 yc는? (단, EI는 일정하다.)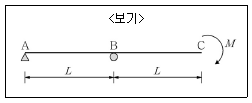
7. <보기>와 같이 P1으로 인한 B점의 처짐 δB1=0.2m, P2로 인한 B점의 처짐 δB2=0.2m이다. P1과 P2가 동시에 작용했을 때 P1이 한 일의 크기는?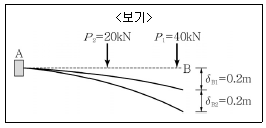
- 4kN ·m
- 8kN · m
- 12kN · m
- 16kN · m
8. <보기>의 그림(a)와 같이 등분포하중과 단부 모멘트하중이 작용하는 단순지지 보의 휨모멘트도는 그림(b)와 같다. 정모멘트 Mp 와 부모멘트 Mn의 차이 MT의 크기는?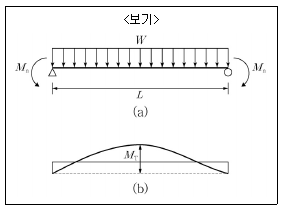
- wL2/24
- wL2/6
- wL2/12
- wL2/8
9. <보기>는 응력과 변형률 곡선을 나타낸 그래프이다. 각 지점의 명칭으로 옳지 않은 것은?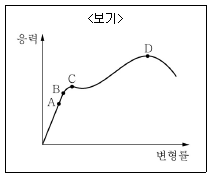
- A점은 비례한도(proportional limit)이다.
- B점은 소성한도(plastic limit)이다.
- C점은 항복점(yield strength)이다.
- D점은 한계응력(ultimate stress)이다.
10. <보기>와 같은 게르버 보에서 B점의 휨모멘트 크기는? (단, 반시계방향은 +, 시계방향은 -이다.)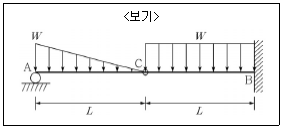
11. <보기>와 같은 보의 반력으로 옳은 것은?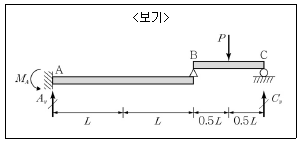
- Ay=0.25P, MA=-PL, Cy=0.5P
- Ay=0.5P, MA=-PL, Cy=0.5P
- Ay=-0.25P, MA=PL, Cy=0.25P
- Ay=0.5P, MA=PL, Cy=0.5P
12. <보기>와 같은 직사각형에서 최소 단면 2차 반경(최소 회전 반경)은? (단, h>b이다.)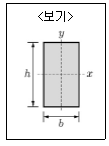
13. <보기>와 같은 부정정 보가 등분포하중을 지지하고 있을 때 B지점 수직반력의 한계는 300kN이다. B지점의 수직 반력이 한계에 도달할 때까지 보에 재하할 수 있는 최대 등분포하중 Wmax의 크기는? (단, EI는 일정하며 단면의 휨성능은 받침 B의 휨성능을 초과한다고 가정한다.)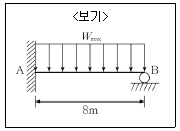
- 50kN/m
- 100kN/m
- 200kN/m
- 300kN/m
14. <보기>와 같이 길이가 7L인 내민보 위로 길이가 L인 등분포하중 W가 이동하고 있을 때 이 보에 발생하는 최대 반력은?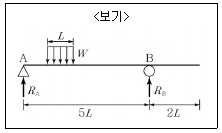
- RA=1.3WL
- RB=0.9WL
- RA=0.9WL
- RB=1.3WL
15. <보기>와 같이 O점에 20kN · m의 모멘트하중이 작용할 때 각 부재의 전달모멘트는?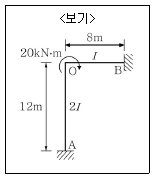
- MAo=11.4kN · m
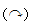 , MBO=8.5kN · m
, MBO=8.5kN · m 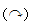
- MAo=5.7kN · m
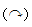 , MBO=4.2kN · m
, MBO=4.2kN · m 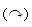
- MAo=8.5kN · m
 , MBO=11.4kN · m
, MBO=11.4kN · m 
- MAo=4.2kN · m
 , MBO=5.7kN · m
, MBO=5.7kN · m 
16. <보기>와 같은 정정라멘구조에 분포하중 W가 작용할 때 최대 모멘트 크기는?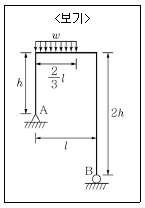
17. 보에 굽힘이 발생하였을 때 보의 상면과 하면사이에 종방향의 길이가 변하지 않는 어떤 면이 존재하는데, 이 면의 이름은?
- 중립면
- 중심면
- 중앙면
- 중간면
18. 균일단면을 가지며 높이가 20m인 콘크리트 교각이 압축하중 P=11MN을 받고 있다. 콘크리트의 허용압축응력이 5.5MPa일 때 필요한 교각의 단면적은? (단, 교각의 자중을 고려하며 콘크리트의 비중량은 25kN/m3이다.)
- 2.0m2
- 2.2m2
- 2.4m2
- 2.6m2
19. 원통형 압력용기에 작용하는 원주방향응력이 16MPa이다. 이때 원통형 압력용기의 종방향응력 크기는?
- 4MPa
- 8MPa
- 16MPa
- 32MPa
20. <보기>와 같이 타원형 단면을 가진 얇은 두께의 관이 비틀림 우력 T=6N · m를 받고 있을 때 관에 작용하는 전단흐름의 크기는? (단,π=3이다.)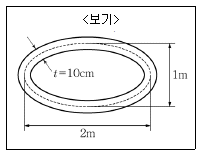
- 20N/m
- 10N/m
- 5N/m
- 2N/m






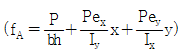
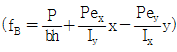
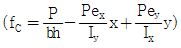
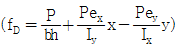
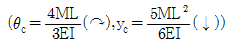
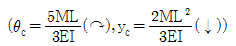
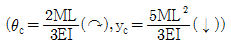
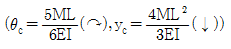
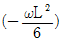
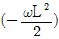
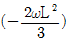
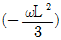
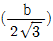
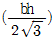
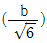
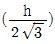
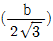 "이 최소 단면 2차 반경이 된다.
"이 최소 단면 2차 반경이 된다. , MBO=4.2kN · m
, MBO=4.2kN · m  "입니다.
"입니다.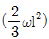
따라서, 동력차가 충돌 후에 스프링에 저장된 운동에너지는 동력차의 운동에너지와 같습니다. 동력차의 운동에너지는 (1/2)mv^2이므로, 스프링에 저장된 운동에너지도 (1/2)mv^2입니다.
스프링에 저장된 운동에너지는 스프링 상수 k와 변위량 x에 비례합니다. 따라서, (1/2)mv^2 = (1/2)kx^2에서 x를 구하면 됩니다.
주어진 스프링 상수 k는 2TN/m이므로, k를 대입하여 방정식을 풀면 x = 0.02m가 됩니다. 따라서, 스프링의 최대 수평 변위량은 0.02m입니다.