1. ＜보기＞와 같은 단면 (a), (b)를 가진 단순보에서 중앙에 같은 크기의 집중하중을 받을 때, 두 보의 최대처짐비(△a/△b)는? (단, 각 단순보의 길이와 탄성계수는 서로 동일하며 (a)의 두 보는 서로 분리되어 있다.)
- 2
- 3
- 4
- 5
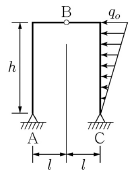
3. ＜보기＞와 같이 구조물에 외력이 (P1=2t, P2=2t, W=3t) 작용하여 평형상태에 있을 때, 합력의 작용선이 x축을 지나는 점의 위치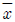 
값(m)은?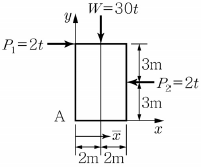
- 2.0m
- 2.2m
- 2.6m
- 2.8m
4. ＜보기＞와 같은 높이가 h인 캔틸레버보에 열을 가하여 윗부분과 아랫부분의 온도 차이가 △T가 되었을 때, 보의 끝점 B에서의 처짐은?
5. ＜보기＞와 같이 트러스의 B점에 연직하중 P가 작용할 때 B점의 연직처짐은? (단, 모든 부재의 축강성도 EA는 일정하다.)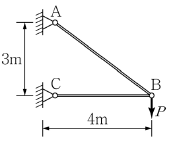
6. ＜보기＞와 같은 원형단면과 튜브단면을 갖는 보에서 원형단면보와 튜브단면 보의 소성모멘트(plastic moment)의 비 (Mp(a)/Mp(b))는? (단, 두 단면은 동일한 강재로 제작되었다.)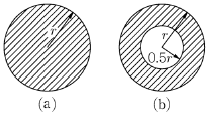
- 15/16
- 8/7
- 6/5
- 4/3
7. ＜보기＞와 같은 비대칭 삼각형 y축에서 도심까지의 거리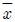 
는?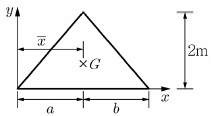
- (a+b)/2
- (a+b)/3
- (a+2b)/2
- (2a+b)/3
8. ＜보기＞와 같은 단면에 4,000kgf⋅cm 비틀림 모멘트(T)가 작용할 때, 최대 전단응력은?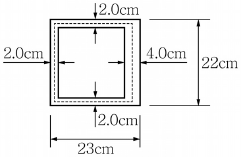
- 2.5kgf/cm2
- 3.5kgf/cm2
- 4.5kgf/cm2
- 5.5kgf/cm2
9. P1이 단순보의 C점에 단독으로 작용했을 때 C점, D점의 수직변위가 각각 4mm, 3mm이었고, P2가 D점에 단독으로 작용했을 때 C점, D점의 수직변위가 각각 3mm, 4mm이었다. P1이 C점에 먼저 작용하고 P2가 D점에 나중에 작용할 때 P1과 P2가 한 전체 일은? (단, P1=P2=4N 이다.)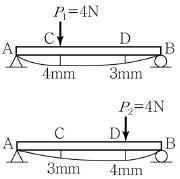
- 22N⋅mm
- 28N⋅mm
- 30N⋅mm
- 32N⋅mm
10. ＜보기＞와 같이 캔틸레버보 AB에서 끝점 B는 강성이 k=9EI/L3인 스프링으로 지지되어 있다. B점에 하중 P가 작용할 때, B점에서 처짐의 크기는? (단, 보의 휨강성도 EI는 전 길이에 걸쳐 일정하다.)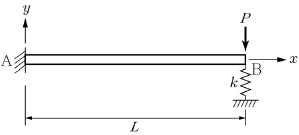
11. ＜보기＞와 같은 한 변의 길이가 자유단에서 b, 고정단에서 2b인 정사각형 단면 봉이 인장력 P를 받고 있다. 봉의 탄성계수가 E일 때, 변단면 봉의 길이 변화량은?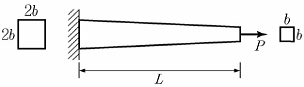
12. ＜보기＞와 같은 평면 트러스에서 B점에서의 반력의 크기와 방향은? (단, √3=1.7로 계산한다.)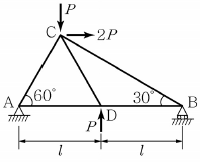
- 0.6P↑
- 0.6P↓
- 1.1P↑
- 1.1P↓
13. ＜보기＞는 상부 콘크리트 슬래브와 하부 강거더로 구성된 합성단면으로 강재와 콘크리트의 탄성계수는 각각 Es=200GPa, Ec=25GPa이다. 이 단면에 정모멘트가 작용하여 콘크리트 슬래브에는 최대 압축응력 5MPa, 강거더에는 최대 인장응력 120MPa이 발생하였다. 합성 단면 중립축의 위치(C)는?
- 150mm
- 160mm
- 170mm
- 180mm
14. 길이가 1m인 축부재에 인장력을 가했더니 길이가 3mm 늘어났다. 축부재는 완전탄소성 재료(perfectly elasto-plastic material)로 항복응력은 200MPa, 탄성계수는 200GPa이다. 인장력을 제거하고 나면 축부재의 길이는?
- 1,000mm
- 1,001mm
- 1,002mm
- 1,003mm
15. ＜보기＞와 같은 길이가 10m인 캔틸레버보에 분포하중 qx=50-10x+x2/2 이 작용하고 있을 때 지점 A에서부터 6m 떨어진 지점 B에서의 전단력 VB의 크기로 가장 옳은 것은?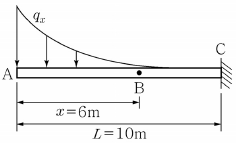
- 84N
- 156N
- 444N
- 516N
16. ＜보기＞와 같은 부정정 기둥의 하중 작용점에서 처짐양은? (단, 축 강성은 EA이다.)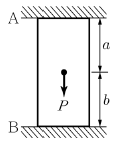
17. ＜보기＞와 같은 정사각형 단면을 갖는 짧은 기둥의 측면에 홈이 패어 있을 때 작용하는 하중 P로 인해 단면 m-n에 발생하는 최대압축응력은?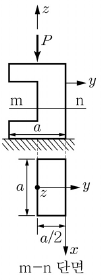
- 2P/a2
- 4P/a2
- 6P/a2
- 8P/a2
18. ＜보기＞와 같이 단순보 위를 이동 하중이 통과할 때, A점으로부터 절대 최대 모멘트가 발생하는 위치는?
19. ＜보기＞와 같은 연속보의 지점 B에서 침하가 δ만큼 발생하였다면 B지점의 휨모멘트 MB는? (단, 모든 부재의 휨 강성도 EI는 일정하다.)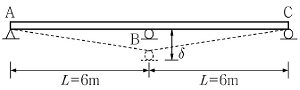
20. A단이 고정이고, B단이 이동단인 부정정보에서 A점 수직 반력의 크기와 방향은?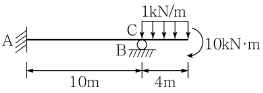
- 2.7kN(↑)
- 2.7kN(↓)
- 3.7kN(↑)
- 3.7kN(↓)
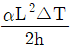
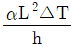
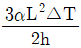
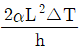
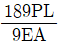
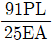
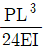
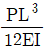
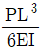
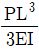
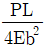
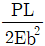
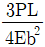
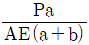
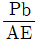
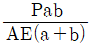
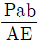
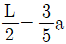
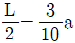
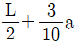
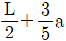
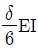
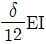
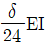
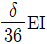
하지만 (b)의 경우, 중앙에서부터 좌우로 거리가 다른 두 지점에서 최대처짐이 발생하게 됩니다. 이때, (b)의 좌측 보는 오른쪽으로 뻗어나가는 형태이므로, 오른쪽 지점에서의 최대처짐이 더 큽니다. 따라서 (a)의 두 지점에서의 최대처짐과 (b)의 오른쪽 지점에서의 최대처짐을 비교하면, (b)의 최대처짐이 더 큽니다.
따라서, 두 보의 최대처짐비(△a/△b)는 (a)의 두 지점에서의 최대처짐과 (b)의 오른쪽 지점에서의 최대처짐을 비교한 값이 됩니다. 이 값은 2/0.5 = 4가 됩니다.