1과목: 과목 구분 없음
1. 자장의 세기가 104/π [A/m]인 공기 중에서 50[cm]의 도체를 자장과 30°가 되도록 하고 60[m/s]의 속도로 이동시켰을 때의 유기기전력은?
- 20mV
- 30mV
- 60mV
- 80mV
2. 어떤 전하가 100[V]의 전위차를 갖는 두 점 사이를 이동하면서 10[J]의 일을 할 수 있다면, 이 전하의 전하량은?
- 0.1C
- 1C
- 10C
- 100C
3. 무한히 긴 직선 도선에 628[A]의 전류가 흐르고 있을 때 자장의 세기가 50[A/m]인 점이 도선으로부터 떨어진 거리는?
- 1m
- 2m
- 4m
- 5m
4. N회 감긴 환상코일의 단면적은 S[m2]이고 평균 길이가 l[m]이다. 이 코일의 권수와 단면적을 각각 두 배로 하였을 때 인덕턴스를 일정하게 하려면 길이를 몇 배로 하여야 하는가?
- 8배
- 4배
- 2배
- 16배
5. <보기>와 같은 RLC병렬회로에서 v=80√2sin(wt)[V]인 교류를 a, b 단자에 가할 때, 전류 I의 실효값이 10[A]라면, Xc의 값은?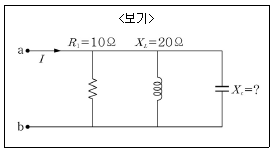
- 8Ω
- 10Ω
- 10√2Ω
- 20Ω
6. <보기>와 같은 회로의 합성저항은?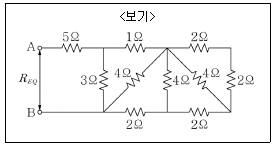
- 8Ω
- 6.5Ω
- 5Ω
- 3.5Ω
7. <보기>와 같이 전류원과 2개의 병렬저항으로 구성된 회로를 전압원과 1개의 직렬저항으로 변환할 때, 변환된 전압원의 전압과 직렬저항 값은?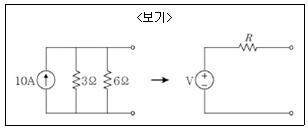
- 10V, 9Ω
- 10V, 2Ω
- 20V, 2Ω
- 90V, 9Ω
8. 저항 R1=1[Ω]과 R2=2[Ω]이 병렬로 연결된 회로에 100[V]의 전압을 가했을 때, R1에서 소비되는 전력은 R2에서 소비되는 전력의 몇 배인가?
- 0.5배
- 1배
- 2배
- 같다
9. <보기>와 같이 저항 R=24[Ω], 유도성 리액턴스 XL =20[Ω], 용량성 리액턴스 XC=10[Ω]인 직렬회로에 실효치 260[V]의 교류전압을 인가했을 경우 흐르는 전류의 실효치는?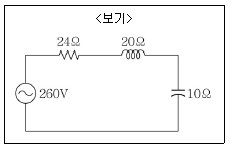
- 5A
- 10A
- 15A
- 20A
10. <보기>와 같은 회로에서 a, b 단자 사이에 60[V]의 전압을 가하여 4[A]의 전류를 흘리고 R1, R2에 흐르는 전류를 1 : 3으로 하고자 할 때 R1의 저항값은?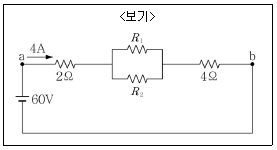
- 6Ω
- 12Ω
- 18Ω
- 36Ω
11. <보기>와 같은 브리지 회로에서 a, b 사이의 전압이 0일 때, R4에서 소모되는 전력이 2[W]라면, c와 d 사이의 전압 Vcd는?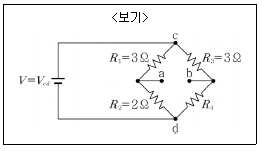
- 1V
- 2V
- 5V
- 10V
12. 10×10-6[C]의 양전하와 6×10-7[C]의 음전하를 갖는 대전체가 비유전율 3인 유체 속에서 1[m] 거리에 있을 때 두 전하 사이에 작용하는 힘은? (단, 비례상수 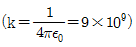 이다.) (문제오류로 인하여 실제 시험에서는 3, 4번이 정답처리 되었습니다. 여기서는 3번을 누르면 정답 처리됩니다.)
이다.) (문제오류로 인하여 실제 시험에서는 3, 4번이 정답처리 되었습니다. 여기서는 3번을 누르면 정답 처리됩니다.)
- -1.62×10-1N
- 1.62×10-1N
- -1.8×10-2N
- 1.8×10-2N
13. 자체 인덕턴스가 각각 L1=10[mH], L2=10[mH]인 두 개의 코일이 있고, 두 코일 사이의 결합계수가 0.5일 때, L1 코일의 전류를 0.1[s] 동안 10[A] 변화시키면 L2에 유도되는 기전력의 양(절댓값)은?
- 10mV
- 100mV
- 50mV
- 500mV
14. 어떤 회로에 v=100√2sin(120πt+π/4)[V]의 전압을 가했더니 i=10√2sin(120πt-π/4)[A]의 전류가 흘렀다. 이 회로의 역률은?
- 0
- 1/√2
- 0.1
- 1
15. <보기>와 같은 회로에서 전류 I의 값은?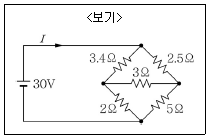
- 6A
- 8A
- 10A
- 12A
16. <보기>와 같은 그림에서 스위치가 t=0인 순간 2번 접점으로 이동하였을 경우 t=0+인 시점과 t=∞가 되었을 때, 저항 5[kΩ]에 걸리는 전압을 각각 구한 것은?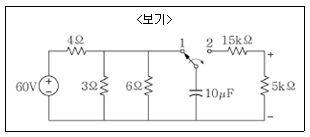
- 5V, 0V
- 7.5V, 1.5V
- 10V, 0V
- 12.5V, 3V
17. <보기>와 같이 R, C소자로 구성된 회로에서 전달함수를 H=Vo/Vi라고 할 때, 회로의 특성으로 옳은 것은?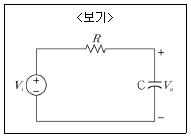
- 고역 통과 필터(High-pass Filter)
- 저역 통과 필터(Low-pass Filter)
- 대역 통과 필터(Band-pass Filter)
- 대역 차단 필터(Band-stop Filter)
18. 진공 중 반지름이 a[m]인 원형도체판 2매를 사용하여 극판거리 d[m]인 콘덴서를 만들었다. 이 콘덴서의 극판거리를 3배로 하고 정전용량을 일정하게 하려면 이 도체판의 반지름은 a의 몇 배로 하면 되는가? (단, 도체판 사이의 전계는 모든 영역에서 균일하고 도체판에 수직이라고 가정한다.)
- 1/3배
- 1/√3배
- 3배
- √3배
19. <보기>와 같이 전압원을 접속했을 때 흐르는 전류 I의 값은?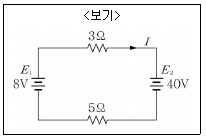
- 4A
- -4A
- 6A
- -6A
20. <보기>와 같은 회로에서 인덕터의 전압 vL 이 t>0 이후에 0이 되는 시점은? (단, 전류원의 전류 i=0, t<0 이고 i=te-2t[A], t≥0이다.)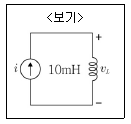
- 1/2S
- 1/5S
- 2s
- 5s






문제에서 전하가 100[V]의 전위차를 갖는 두 점 사이를 이동하면서 10[J]의 일을 할 수 있다고 했으므로, 일(W) = 10[J], 전위차(V) = 100[V] 입니다. 이를 위의 식에 대입하면 10[J] = Q × 100[V] 이 됩니다. 따라서 전하량(Q) = 10[J] ÷ 100[V] = 0.1[C] 가 됩니다.
따라서 정답은 "0.1C" 입니다.