1과목: 과목 구분 없음
1. 지적측량의 성격에 대한 다음 설명 중 옳지 않은 것은?
- 법률로 정해진 측량방법 및 절차에 의해 측량한다는 점에서 기속측량의 성격을 가진다.
- 토지에 대한 물권이 미치는 범위, 위치, 양을 결정한다는 점에서 사법측량의 성격을 가진다.
- 지적측량성과는 영구히 보존된다는 점에서 영구성을 가진다.
- 지구의 곡률을 고려하여 측량하는 지역을 타원체면으로 간주하여 실시하는 측지측량의 성격을 가진다.
2. 다음 중 지적도근점측량을 반드시 실시하는 경우로 적절치 않은 것은?
- 도시 외 지역에서 세부측량을 하는 경우
- 도시개발사업 등으로 인하여 확정측량을 하는 경우
- 축척변경을 위한 측량을 하는 경우
- 측량지역의 면적이 해당 지적도 2장에 해당되는 면적인 경우
3. 다음 지적재조사측량에 관한 사항 중 옳지 않은 것은?
- 기초측량은 위성측량 및 토털스테이션측량으로 한다.
- 세부측량은 위성측량, 토털스테이션측량 및 항공사진측량 등의 방법으로 한다.
- 지적소관청은 위성측량, 토털스테이션측량 및 항공사진측량 방법 등으로 지적재조사측량성과(지적기준점측량성과는 제외)의 정확성을 검사하여야 한다.
- 경계점의 지적재조사측량성과와 지적재조사측량성과에 대한 검사의 연결교차가 ±0.1m 이내이면 지적재조사측량성과를 최종 측량성과로 결정한다.
4. 평판측량방법에 따른 세부측량을 도선법으로 하는 경우 도선의 변은 ( ㉠ ) 이하여야 하며 도상에 영향을 미치지 아니하는 지상거리의 축척별 허용범위는 ( ㉡ )로 한다. ㉠, ㉡에 들어갈 말로 옳은 것은? (단, M은 축척분모이다.)
- ㉠ 20개, ㉡ (M/5)mm
- ㉠ 20개, ㉡ (M/10)mm
- ㉠ 30개, ㉡ (M/5)mm
- ㉠ 30개, ㉡ (M/10)mm
5. 지번 및 지목을 제도할 때 지번의 글자 간격은 얼마를 기준으로 띄어서 제도하여야 하는가?
- 글자크기의 1/2정도
- 글자크기의 1/3정도
- 글자크기의 1/4정도
- 글자크기의 1/5정도
6. 구소삼각측량에 대한 설명으로 옳지 않은 것은?
- 원점의 수치는 X=10,000, Y=10,000을 사용하였다.
- 대삼각측량을 미리 실시하지 않고 시행하였다.
- 거리의 단위는 간으로 하였다.
- 27개의 지역에 대해 독립적으로 실시하였고, 총 11개의 원점이 있었다.
7. 경위의측량방법과 교회법에 따른 지적삼각보조점의 관측에 대한 기준으로 옳은 것은?
- 관측은 10초독 이상의 경위의를 사용한다.
- 수평각 관측은 2대회 방향관측법을 따른다.
- 삼각형 내각관측의 합과 180도와의 차는 ±40초 이내여야 한다.
- 기지각과 수평각의 측각공차는 ±40초 이내여야 한다.
8. 어떤 각을 9회 관측한 결과 ±0.6″의 평균제곱근오차(중등오차)를 얻었다. 같은 정확도로 해서 ±0.3″의 평균제곱근오차를 얻으려면 관측횟수는?
- 18회
- 24회
- 30회
- 36회
9. 측량의 오차특성에 대한 설명으로 옳지 않은 것은?
- 우연오차는 확률법칙에 따르고 정오차는 측정횟수에 비례하여 누적된다.
- 직접 측정한 거리나 각을 변수로 하는 함수에 의해 계산된 값의 오차는 직접 측정량의 오차로부터 오차전파법칙에 따라 구할 수 있다.
- 직사각형 토지의 가로변과 세로변의 길이를 여러 번 측정하여 최확값 x=10m, y=20m, 각각의 표준오차 σx=0.02m, σy=0.03m를 얻었다면 이 토지 면적의 표준오차는 0.05m2이다.
- 삼각수준측량에서 경사거리와 연직각을 관측하여 높이차 및 그 표준오차를 구할 때 각의 오차는 라디안 단위로 환산하여 적용한다.
10. 지적도근점측량에서 지적도근점을 구성하는 도선형태 기준에 해당하지 않는 것은?
- 개방도선
- 폐합도선
- 왕복도선
- 다각망도선
11. 다음 중 지적측량 시 도근점 성과표에 반드시 기록하지 않아도 되는 것은?
- 좌표와 직각좌표계 원점명
- 소재지와 측량연월일
- 설치기관
- 표고
12. 다음 경위의측량방법에 따른 세부측량의 관측 및 계산 중 옳지 않은 것은?
- 도선법 또는 방사법에 따를 것
- 수평각의 측각공차는 1방향각일 때 40초 이내로 할 것
- 수평각의 관측은 1대회의 방향관측법이나 2배각의 배각법에 따를 것
- 수평각의 측각공차는 1회 측정각과 2회 측정각의 평균값에 대한 교차를 40초 이내로 할 것
13. 전자파 및 광파기 측량방법에 따라 다각망도선법으로 지적삼각보조점측량을 할 때 1도선의 거리는 ( ㉠ ) 이하로 하고 1도선의 점의 수는 기지점과 교점을 포함하여 ( ㉡ )이하로 하여야 한다. ㉠ , ㉡ 에 들어갈 말로 옳은 것은?
- ㉠ 2km, ㉡ 3개
- ㉠ 3km, ㉡ 4개
- ㉠ 4km, ㉡ 5개
- ㉠ 5km, ㉡ 6개
14. 평면거리 계산 시 아래 약도를 참조한 연직각에 의한 계산방식 중에서 기준면의 거리를 구하는 공식은?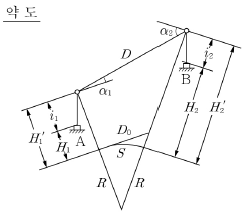
15. 라플라스(Laplace)점에 대한 설명으로 옳은 것은?
- 구소삼각점을 설치할 때 사용한 점이다.
- GPS측량의 상시관측소가 설치된 점이다.
- 삼각망의 비틀림을 바로 잡을 수 있는 점이다.
- 복합다각망의 조정에 필요한 점이다.
16. 배각법에 의한 지적도근점의 각관측에서 1도선의 폐색오차는 최대 얼마 이내여야 하는가? (단, 폐색변을 포함한 변의 수가 9개이며 2등도선이다.)
- ±30초 이내
- ±60초 이내
- ±90초 이내
- ±120초 이내
17. 도면의 축척이 1/600인 지역을 1/3,000로 잘못 측정한 결과 면적이 500m2였을 때 올바른 면적은?
- 15m2
- 20m2
- 25m2
- 30m2
18. 다음 그림과 같은 수치(좌표)측량의 원과 직선 교차점 계산식 중 옳지 않은 것은?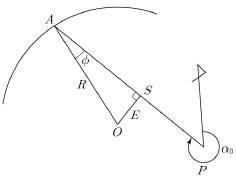
- 수선장 E=(PY-OY)cosα0-(Px-Ox)sinα0
- ϕ=cos-1(E/R)
- 방위각 VOA=VPA±ϕ
- AX=OX+R⋅cosVOA
19. 다음 그림과 같은 수치(좌표)측량의 직선과 직선 교차점 계산식 중 옳지 않은 것은?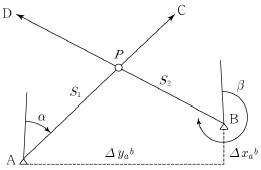
- PY=AY+S1⋅cosα
- AX+S1⋅cosα=BX+S2⋅cosβ
- S1⋅sinα-S2⋅sinβ=BY-AY
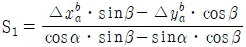
20. 도근측량에서 다각망도선법의 상관방정식이 아래 표와 같을 때 방위각의 표준방정식 A항과 B항에 들어갈 각각의 값은?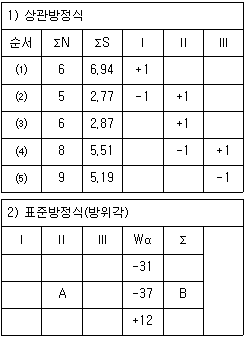
- A: -5, B: -25
- A: 11, B: 38
- A: 19, B: -31
- A: 17, B: 20






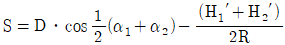
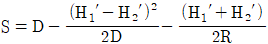
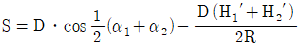
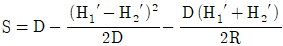
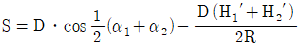 " 입니다.
" 입니다.
"지구의 곡률을 고려하여 측량하는 지역을 타원체면으로 간주하여 실시하는 측지측량의 성격을 가진다."는 옳은 설명입니다. 지구는 구형이 아니기 때문에 지적측량에서는 지구의 곡률을 고려하여 측량을 실시합니다. 이를 위해 지역별로 타원체면을 설정하여 측량을 실시합니다. 이러한 방식은 측지측량의 성격을 가지며, 지적도 작성에 사용됩니다.