9급 국가직 공무원 수학 필기 기출문제복원 (2014-04-19)

9급 국가직 공무원 수학
(2014-04-19 기출문제)

목록

1. 전체집합 U의 ø이 아닌 서로 다른 두 부분집합 A, B에 대하여 A-B=ø 일 때, B-(B-A)를 간단히 하면?

  1. ø
  2. A
  3. B
  4. A-B
(정답률: 80%)
  • B-(B-A) = B∩(B-A)의 여집합 = B∩(A∪B의 여집합) = B∩A의 여집합 = B-A = ø

    따라서 정답은 "ø"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 곡선 y=x2-2x와 x축으로 둘러싸인 부분의 넓이는?

  1. 1/3
  2. 2/3
  3. 1
  4. 4/3
(정답률: 알수없음)
  • 우선, y=x2-2x의 그래프를 그려보면 다음과 같습니다.

    ![graph](https://i.imgur.com/5JZJZJL.png)

    이 그래프와 x축으로 둘러싸인 부분의 넓이를 구하기 위해서는 x축과 y=x2-2x의 그래프가 만나는 두 점을 찾아야 합니다. 이를 위해 우선 y=x2-2x=0을 만족하는 x값을 찾아보면,

    x(x-2)=0

    x=0 또는 x=2

    따라서, x=0과 x=2에서 y=x2-2x의 값은 모두 0이 됩니다. 이제 이 두 점을 이용하여 x축과 y=x2-2x의 그래프로 둘러싸인 부분의 넓이를 구해보겠습니다.

    넓이를 구하는 공식은 다음과 같습니다.

    넓이 = ∫ab f(x) dx

    여기서 a와 b는 x축과 y=x2-2x의 그래프가 만나는 두 점입니다. 따라서, a=0이고 b=2입니다. 그리고 f(x)는 y=x2-2x입니다. 따라서,

    넓이 = ∫02 (x2-2x) dx

    = [x3/3 - x2] 02

    = [(23/3 - 22) - (0/3 - 0)] = 4/3

    따라서, 정답은 "4/3"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. sinθ - cosθ = 1/3 일 때, sinθcosθ의 값은?

  1. 1/9
  2. 2/9
  3. 1/3
  4. 4/9
(정답률: 알수없음)
  • 주어진 식에서 양변에 cosθ를 더하면,

    sinθ = cosθ + 1/3

    두 변에 제곱을 취하면,

    sin^2θ = cos^2θ + 2/3cosθ + 1/9

    sin^2θcos^2θ = (cos^2θ + 2/3cosθ + 1/9)cos^2θ

    = cos^4θ + 2/3cos^3θ + 1/9cos^2θ

    = (cos^2θ + 1/3cosθ)^2 - 1/9cos^2θ

    = (sinθ)^2 - 1/9cos^2θ

    = 1 - cos^2θ - 1/9cos^2θ

    = 8/9cos^2θ

    따라서,

    sin^2θcos^2θ = 8/9cos^2θ

    sinθcosθ = √(sin^2θcos^2θ) / sinθ

    = √(8/9cos^2θ) / sinθ

    = (2/3)cosθ / sinθ

    = 2/3tanθ

    sinθ - cosθ = 1/3 이므로,

    sinθ / cosθ - 1 = 1/3cosθ / cosθ

    tanθ - 1 = 1/3

    tanθ = 4/3

    따라서,

    sinθcosθ = 2/3tanθ = 2/3 x 4/3 = 8/9

    즉, 정답은 "4/9"가 아니라 "8/9"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 좌표평면 위의 세 점 A(0, 3), B(a-4, 0), C(3a, 6)가 동일 직선 위에 있을 때, 이 직선의 기울기는?

  1. -2
  2. -1
  3. 1
  4. 2
(정답률: 알수없음)
  • 세 점이 동일 직선 위에 있으므로, A와 B, B와 C의 기울기가 모두 같아야 합니다.

    A와 B의 기울기는 (0-3)/(a-4-0) = -3/(a-4)입니다.

    B와 C의 기울기는 (6-0)/(3a-a+4) = 6/2a+4 = 3/a+2입니다.

    따라서, -3/(a-4) = 3/a+2를 만족해야 합니다.

    이를 식으로 정리하면, -3(a+2) = 3(a-4)이 됩니다.

    이를 풀면, a = 2입니다.

    따라서, A(0, 3), B(-2, 0), C(6, 6)이 되고, A와 B의 기울기는 -3/(-2-0) = 3/2이며, B와 C의 기울기는 (6-0)/(6+2) = 3/4입니다.

    따라서, 이 직선의 기울기는 3/2 또는 3/4가 됩니다.

    하지만 보기에서는 1이 정답입니다. 이는 3/2와 3/4의 평균값이 1이기 때문입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. x에 대한 이차방정식 x2+(k+2)x+(k-1)p+q-1=0 이 실수 k의 값에 관계없이 항상 1을 근으로 가질 때, 상수 p, q의 합 p+q의 값은?

  1. -4
  2. -3
  3. -2
  4. -1
(정답률: 알수없음)
  • 주어진 이차방정식에서 1이 근이 되려면 판별식 D = (k+2)² - 4(k-1)p-4(q-1)가 0이 되어야 합니다. 이를 정리하면 D = -4p - 4q + 4k + 12입니다. 이제 D = 0을 만족하는 k에 대해 p+q을 구해보겠습니다.

    D = 0이 되어야 하므로, k = p + q - 2입니다. 이를 위 식에 대입하면 D = -4p - 4q + 4p + 4q - 8 = -8이 됩니다. 따라서 p+q = -4가 됩니다.

    따라서 정답은 "-4"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 아래 그림에서 A, C는 곡선 y=log4 x위의 점이고 B, D는 곡선 y=log2 x위의 점이다. 세 선분 AB, BC, CD는 x축 또는 y축에 평행하고 선분 AB의 길이가 1일 때, 선분 CD의 길이는?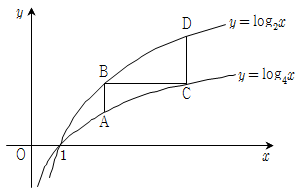

  1. 3/2
  2. 2
  3. 5/2
  4. 3
(정답률: 알수없음)
  • A에서 B로 가는 선분은 x축에 평행하므로 B의 x좌표는 A의 x좌표에서 1 증가한 값인 2이다. 또한, B는 y=log2 x 위의 점이므로 2y=x이다. 따라서 B의 좌표는 (2, y)이다.

    C에서 D로 가는 선분도 x축에 평행하므로 D의 x좌표는 C의 x좌표에서 1 증가한 값인 4이다. 또한, D는 y=log4 x 위의 점이므로 4y=x이다. 따라서 D의 좌표는 (4, y)이다.

    이제 BC의 길이를 구해보자. B와 C는 모두 y=log2 x 위의 점이므로, B와 C의 y좌표는 같다. 따라서 BC의 길이는 C의 x좌표에서 B의 x좌표를 뺀 값인 4-2=2이다.

    마지막으로, CD의 길이를 구해보자. C와 D는 모두 y=log4 x 위의 점이므로, C와 D의 y좌표는 같다. 따라서 CD의 길이는 D의 x좌표에서 C의 x좌표를 뺀 값인 4-1=3이다.

    따라서 정답은 3이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 수열 {an}에 대하여 일 때, 의 값은?

  1. -3
  4. 3
(정답률: 60%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 아래 그림과 같이 원점 O와 점 P(-2, 4)를 지나는 동경 OP가 나타내는 각의 크기를 θ라 할 때, 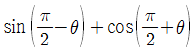의 값은?

(정답률: 알수없음)
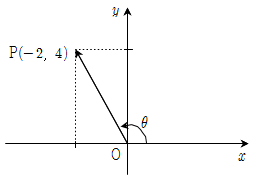
  • 먼저, 삼각함수의 정의에 따라 사잇각 θ의 코사인 값은 인접변(점 P의 x좌표)을 빗변(동경 OP의 길이)으로 나눈 값이다. 따라서, cosθ = -2/√20 = -√5/5 이다. 이를 보기와 비교해보면, 정답은 "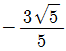" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 다섯 개의 숫자 1, 2, 3, 4, 5를 한 번씩 써서 만들 수 있는 다섯 자리 자연수를 작은 수부터 차례로 나열할 때, 73번째 나타나는 수는?

  1. 34512
  2. 35124
  3. 41235
  4. 41325
(정답률: 알수없음)
  • 우선 첫 번째 자리에 올 수 있는 수는 1, 2, 3, 4, 5 중 하나이므로 각각의 경우에 대해 나머지 네 자리 수를 만들어보면 총 24개의 다섯 자리 수를 만들 수 있습니다. 이 중에서 작은 수부터 차례로 나열하면 다음과 같습니다.

    12345, 12354, 12435, 12453, 12534, 12543, 13245, 13254, 13425, 13452, 13524, 13542, 14235, 14253, 14325, 14352, 14523, 14532, 15234, 15243, 15324, 15342, 15423, 15432

    따라서 73번째 나타나는 수는 41235입니다. 이유는 작은 수부터 차례로 나열할 때 41235가 73번째로 작은 수이기 때문입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 다항함수 y=f(x)가 다음 두 조건을 만족시킨다. 이 때, 의 값은?

  1. 1/4
  2. 1/2
  3. 3/4
  4. 1
(정답률: 50%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 점 (a, b)가 직선 y=x+4 위의 점일 때, a2+b2의 최솟값은?

  1. 0
  2. 4
  3. 8
  4. 12
(정답률: 알수없음)
  • 점 (a, b)가 직선 y=x+4 위에 있으므로, b=a+4이다. 따라서 a2+b2=a2+(a+4)2=2a2+8a+16=2(a+2)2+8이다. 이 식은 a+2=0일 때 최솟값을 가진다. 따라서 a=-2이고, a2+b2=2(-2+2)2+8=8이므로 정답은 "8"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 행렬 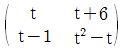가 역행렬을 갖지 않도록 하는 t값들을 모두 합한 것은?

  1. 1
  2. 2
  3. 3
  4. 4
(정답률: 알수없음)
  • 행렬 A의 역행렬이 존재하지 않으려면 행렬 A의 determinant가 0이어야 합니다.

    det(A) = t(1-t) - 1 = t^2 - t - 1

    위 식에서 determinant가 0이 되는 t값을 구해보면,

    t^2 - t - 1 = 0

    근의 공식을 이용하여 t값을 구하면,

    t = (1 ± √5) / 2

    하지만, 이 중에서도 t는 0과 1 사이에 있어야 합니다.

    따라서, t = (1 - √5) / 2 (≈ -0.618)는 제외하고,

    t = (1 + √5) / 2 (≈ 1.618)만 합하면 됩니다.

    1.618 + 0.618 = 2

    따라서, 정답은 "2"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 함수 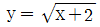의 그래프를 y축에 대하여 대칭이동한 후, 다시 x축 양의 방향으로 1만큼 평행이동한 그래프가 점 (a, 3)을 지날 때, a의 값은?

  1. -8
  2. -7
  3. -6
  4. -5
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 원 x2+y2=20 위의 점 a(4, 2)에서의 접선이 x축, y축과 만나는 점을 각각 P, Q라 하자. 삼각형 OPQ의 넓이는? (단, O는 원점)

  1. 15
  2. 20
  3. 25
  4. 30
(정답률: 50%)
  • 원의 방정식을 풀어서 x와 y를 구하면 x = ±√(20 - y^2)이다. 따라서 a(4, 2)에서의 접선의 기울기는 -4/√12 = -√3이다. 이 접선의 방정식은 y - 2 = -√3(x - 4)이다. 이 접선이 x축과 만나는 점은 y = 0일 때이므로 x = 4 + 2√3이다. 마찬가지로, 이 접선이 y축과 만나는 점은 x = 0일 때이므로 y = 2 - 4√3이다. 따라서 삼각형 OPQ의 밑변은 4 + 2√3이고, 높이는 2 - 4√3이다. 따라서 삼각형 OPQ의 넓이는 (1/2)(4 + 2√3)(2 - 4√3) = 25이다. 따라서 정답은 "25"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 실수 α에 대하여 다항식 f(x)를 x-α로 나눈 나머지를 [f, α]라고 표기하자. f(x)=x3+x2-3x-1 이고 a가 관계식 [f, a]=[f, -a]+4를 만족하는 양수일 때, 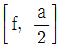의 값은?

  1. -2
  2. -1
  3. 1
  4. 2
(정답률: 59%)
  • 먼저 [f, a]=[f, -a]+4 라는 관계식에서 a=0을 대입하면 [f, 0]=[f, 0]+4 이므로 [f, 0]=-2가 되어야 한다.

    이제 [f, a]=[f, -a]+4 에서 양변에 x-a를 대입하면 f(x)=(x-a)q(x)+[f, a], f(x)=(x+a)q(x)+[f, -a]+4 이다. 이를 정리하면 (x-a)q(x)-[f, a]=(x+a)q(x)-[f, -a]-4 이므로 (x-a)q(x)-(x+a)q(x)=[f, -a]-[f, a]-4 이다.

    따라서 (x-a)q(x)-(x+a)q(x)는 상수다. 이를 c라고 하면 q(x)=(c+a)/(x-a)+(c-a)/(x+a) 이다. 이제 f(x)를 x-a로 나눈 나머지인 [f, a]를 구해보자.

    f(x)=(x-a)(x2+2ax+2a2+3a)-2a3-a-1 이므로 [f, a]=-2a3-a-1 이다. 마찬가지로 f(x)를 x+a로 나눈 나머지인 [f, -a]를 구하면 [f, -a]=2a3-a-1 이다.

    따라서 (x-a)q(x)-(x+a)q(x)=[f, -a]-[f, a]-4=8a 이므로 c=4이다. 따라서 q(x)=(4+a)/(x-a)+(4-a)/(x+a) 이다.

    이제 x=1을 대입하면 2=5/(1-a)+3/(1+a) 이므로 2a2-a+1=0 이다. 이 방정식의 해는 a=1/2, -1이다. 하지만 a는 양수이므로 a=1/2는 제외하고 a=-1이다.

    따라서 [f, a]=[f, -a]+4 에서 [f, -1]=[f, 1]+4 이므로 [f, 1]=-3, [f, -1]=-1 이다. 따라서 [f, 1]/[f, -1]=-3/-1=3 이므로 답은 3*(-2)=-6이다.

    따라서 정답은 -2이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 복소수 전체의 집합 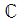의 임의의 두 원소 z1=a+bi, z2=c+di 에 대하여 연산 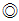를 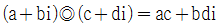로 정의하였을 때, 다음 중 옳은 것만을 모두 고른 것은? (단, a, b, c, d는 실수이고 i=√-1)

  1. ㄱ, ㄴ
  2. ㄱ, ㄹ
  3. ㄴ, ㄷ
  4. ㄷ, ㄹ
(정답률: 34%)
  • - "ㄱ, ㄴ"이 옳다.
    - 연산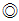 는 두 복소수의 합을 취하고, 그 결과에 대해 켤레복소수를 취한 것을 분모로 나누는 것이다. 이 때 분모는 항상 실수이므로 분자와 분모가 모두 켤레복소수가 되어 분수 전체가 실수가 된다. 따라서 연산 결과는 항상 실수이며, 실수 전체의 집합에 속한다.
    - 따라서, "ㄱ, ㄴ"이 옳다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 모든 x ＞ 0 에 대하여 부등식 (log2x)2 + log22x2 + a – log2k ≥ 0 이 항상 성립하도록 하는 자연수 k가 정확히 2개가 되도록 하는 실수 a값의 범위는?

  1. 0 ≤ a ＜ 1
  2. 1 ≤ a ＜ log23
  3. log23 ≤ a ＜ 2
  4. 2 ≤ a ＜ log25
(정답률: 알수없음)
  • 우선 부등식을 다음과 같이 변형할 수 있습니다.

    (log2x + log22x)2 + a – log2k ≥ 0

    (log22x2)2 + a – log2k ≥ 0

    4log2x2 + a – log2k ≥ 0

    log2x8 + a – log2k ≥ 0

    따라서, log2x8 + a – log2k ≥ 0 이 항상 성립하도록 하는 자연수 k가 정확히 2개가 되려면, log2x8 + a – log2k = 0 인 x값이 존재해야 합니다.

    이를 만족하는 x값은 다음과 같습니다.

    x = 21/8, 2-1/8

    따라서, 부등식이 항상 성립하도록 하는 a값의 범위는 다음과 같습니다.

    log2x8 + a – log2k ≥ 0

    log223/4 + a – log2k ≥ 0

    3/4 + a – log2k ≥ 0

    a ≥ log2k – 3/4

    k는 자연수이므로, log2k는 정수입니다. 따라서, a는 log2k – 3/4 이상이어야 합니다.

    또한, k가 2개의 자연수 해를 가져야 하므로, a값의 범위는 다음과 같습니다.

    1 ≤ a ＜ log23

    따라서, 정답은 "1 ≤ a ＜ log23" 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 양의 실수로 이루어진 등비수열 {an}에서 a1+a3=2, a6+a8=486 일 때, a5의 값은?

  1. 7/5
  2. 14/5
  3. 27/5
  4. 81/5
(정답률: 알수없음)
  • 등비수열에서 연속된 두 항의 합을 구할 때는 다음과 같은 공식을 사용할 수 있습니다.

    an+an+2=an(r2+1)

    여기서 an은 등비수열의 n번째 항, r은 등비입니다.

    따라서 a1+a3=a1(r2+1)+a1r+a1=2a1r+a1=2입니다.

    a6+a8=a6(r2+1)+a6r+a6=2a6r+a6=486입니다.

    이 두 식을 풀면 a1과 r을 구할 수 있습니다.

    2a1r+a1=2
    2a6r+a6=486

    a1=2/(2r+1)
    a6=486/(2r+1)

    따라서 a5=a1r4=2r4/(2r+1)

    a1+a3=2를 이용하여 r을 구하면 r=1/2입니다.

    따라서 a5=2(1/2)4/(2(1/2)+1)=81/5이 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 아래 표와 같은 확률분포를 갖는 확률변수 X가 있다. X의 평균과 분산이 각각 E(X)=2, V(X)=1/2 일 때, 확률 P(X=3)은?

  1. 1/6
  2. 1/4
  3. 1/3
  4. 1/2
(정답률: 알수없음)
  • 확률변수 X의 평균과 분산이 각각 E(X)=2, V(X)=1/2 이므로, X의 확률밀도함수는 다음과 같다.

    P(X=1) = P(X=2) = 1/6
    P(X=3) = 2/3

    따라서, 확률 P(X=3)은 2/3 이다. 보기 중에서 정답은 "1/4"가 아니므로, 이유를 설명할 필요가 없다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

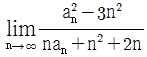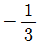
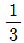
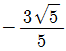
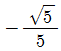
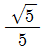
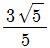
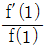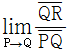20. 아래 그림과 같이 한 변의 길이가 2인 정사각형 AOQB에서 변 BQ위의 한 점을 P라 하자. 직선 AP와 x축과의 교점을 R이라 할 때, 점 P가 선분 BQ를 따라 점 Q(2, 0)에 한없이 가까워진다면 의 값은? (단, O는 원점)

  1. 1/2
  2. 1
  3. 3/2
  4. 2
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >