1과목: 과목 구분 없음
1. 집합 A={1, 2, 3, 4}와 집합 B={1, 4, 7}에 대하여 다음 설명 중 옳은 것은?
- 집합 A와 B는 서로소이다.
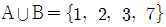
- A – B = {2}
- B – A = {7}
2. 두 집합 X={1, 2, 3}, Y={1, 2, 3, 4}에 대하여 X에서 Y로의 함수인 것만을 모두 고른 것은?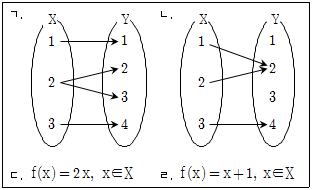
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄹ
- ㄴ, ㄷ, ㄹ
3. 직선 2x-y+1=0을 x축의 방향으로 a만큼, y축의 방향으로 b만큼 평행이동하였더니 직선 2x-y-4=0과 일치하였다. 이때 2a-b의 값은?
- 8
- 7
- 6
- 5
4. 등식  를 만족하는 두 실수 a, b에 대하여 a2-b2의 값은? (단, i = √-1)
를 만족하는 두 실수 a, b에 대하여 a2-b2의 값은? (단, i = √-1)
- -10
- -8
- 8
- 10
5. 함수 f(x)=2x+1 에 대하여 일차함수 g(x)가 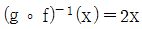 를 만족할 때, g(2)의 값은?
를 만족할 때, g(2)의 값은?
6. 연립이차방정식 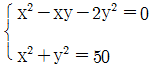 의 해를
의 해를 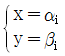 라 할 때, αi+βi의 최댓값은? (단, i = 1, 2, 3, 4)
라 할 때, αi+βi의 최댓값은? (단, i = 1, 2, 3, 4)
- 0
- √10
- 2√10
- 3√10
7. 행렬 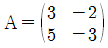 에 대하여
에 대하여  의 모든 성분의 합은?
의 모든 성분의 합은?
- 2
- 1
- -1
- -2
8. 자연수 n에 대하여 부등식 n-1 ≤ log5 A < n 을 만족하는 자연수 A의 개수를 an 이라 할 때, 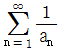 의 값은?
의 값은?
- 3/16
- 5/16
- 7/16
- 9/16
9. 함수 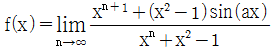 가 실수 전체의 집합에서 연속함수가 되도록 하는 양수 a의 최솟값은?
가 실수 전체의 집합에서 연속함수가 되도록 하는 양수 a의 최솟값은?
- π/6
- π/4
- π/3
- π/2
10. 기울기가 양수인 직선 y=mx+n이 두 원 x2+y2=1, (x-3)2+y2=1 에 동시에 접할 때, 두 상수 m, n의 곱 mn의 값은?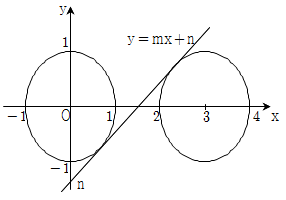
11. 다항식 x3-2x2-4x+2 를 일차식 x+2로 나누었을 때의 나머지는?
- 6
- 2
- -2
- -6
12.  의 값은?
의 값은?
- 485
- 490
- 495
- 500
13. 지수방정식 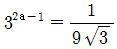 을 만족하는 a의 값은?
을 만족하는 a의 값은?
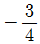
- -1
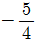
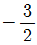
14. 분수함수 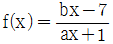 에 대하여 f(1)=-1, f-1(1)=4 일 때, 두 상수 a, b의 곱 ab의 값은? (단, x > 0)
에 대하여 f(1)=-1, f-1(1)=4 일 때, 두 상수 a, b의 곱 ab의 값은? (단, x > 0)
- 6
- 8
- 10
- 12
15. 두 사건 A, B에 대하여 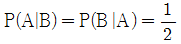 ,
, 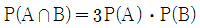 가 성립할 때,
가 성립할 때,  의 값은? (단, P(A)≠0, P(B)≠0)
의 값은? (단, P(A)≠0, P(B)≠0)
- 1/4
- 5/12
- 7/12
- 3/4
16. 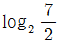 의 정수 부분을 x, 소수 부분을 y라 할 때,
의 정수 부분을 x, 소수 부분을 y라 할 때, 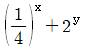 의 값은?
의 값은?
- 3/2
- 2
- 5/2
- 3
17. 확률변수 X가 정규분포 N(50, 152)을 따를 때, 주어진 표준정규분포표를 이용하여 구한 확률 P(X≥80)의 값은?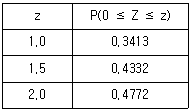
- 0.0228
- 0.0668
- 0.3413
- 0.4772
18. x에 대한 이차방정식 x2+2xcosθ+sin2θ=0 이 중근을 가질 때, tanθ의 값은? (단, 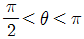 )
)
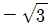
- -1
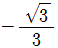
19. 열린 구간 (-5, 15)에서 정의된 미분가능한 함수 f(x)에 대하여, 도함수 y=f′(x)의 그래프가 그림과 같다. 함수 f(x)가 극댓값을 갖는 x의 개수를 a, 극솟값을 갖는 x의 개수를 b라 할 때, a-b의 값은?
- -1
- 0
- 1
- 2
20. 점 (1, 2)를 지나고 기울기가 m인 직선과 곡선 y=x2으로 둘러싸인 부분의 넓이를 S(m)이라 하자. S(m)의 최솟값이 q/p일 때, p+q의 값은? (단, p, q는 서로소인 자연수)
- 7
- 8
- 9
- 10






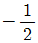
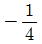
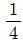
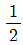
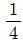 "이다.
"이다.
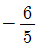
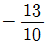
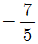
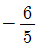 " 이다.
" 이다.
이유는 집합 B에서 집합 A의 원소를 뺀 결과는 {7}이다. 즉, B와 A는 공통된 원소인 1과 4를 가지고 있지만, B에만 있는 원소인 7이 B – A의 결과로 나타난다.